Построение линии пересечения двух плоскостей

Прямая линия, получаемая при взаимном пересечении двухплоскостей, определяется двумя точками, каждая из которых одновременно принадлежит обеим плоскостям.

На рис. 3.37 плоскость общего положения, заданную тре-угольником АВС, пересекает фронтально - проецирующая плоскость, заданная треугольником DEF, Так как треугольник DEF проецируется на плоскость V в виде прямой линии D"F", то фронтальная проекция линии пересечения обеих плоскостей представляют собой отрезок K₁"K2". Находим его горизонталь-ную проекцию и определяем видимость.

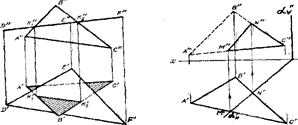
Рис.3.37 Рис.3.38

Горизонтально проецирующая плоскость а пересекает плоскость треугольника АВС (рис, 3.3 8), Горизонтальная проекция линии пересечения этих плоскостей представляет из себя отрезок M'N', который определяется на следе оси'.

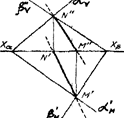Если плоскости заданы следами на плоскостях проекций, то, токи, определяющие прямую пересечения плоскостей} следует выбирать в точках пересечения одноименных следов плоскостей (рис.3.39); прямая, проходящая через эти точки, общие для обеих плоскостей, - их линия пересечения. Поэтому для построения проекций линии пересечения плоскостей a и b необходимо:

1) найти точку М' в пересечении следов aн' и bн' и точку N" в пересечении a_n¢ ¢и b_n¢¢, а по ним проекции М" и N'.

2) провести прямые линии M¢¢N¢¢ и M'N'.

Рис.3.39

Точки пересечения одноименных следов плоскостей являются следами линии пересечения этих плоскостей.

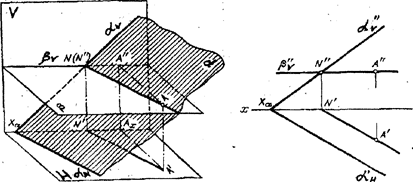Рис.3.40

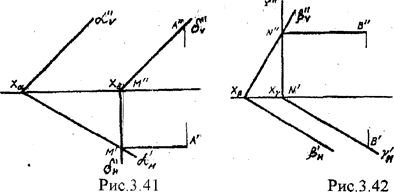
На рис.3.40 пересекаются плоскости a и b. Плоскость a плоскость общего положения, Плоскость b - горизонтальная плоскость. Для построения линии пересечения необходимо:

1) найти точку N" в пересечении следов an¢¢ и bv¢¢;

2) провести через эту точку прямую, исходя из положения

плоскостей и их следов.

На рисунках (3.40 - 3.42) показаны случаи, когда известно направление линии пересечения. Поэтому достаточно иметь лишь одну точку от пересечения следов и, затем, провести через эту точку прямую, исходя из положения плоскостей и их следов.