Машинные методы умножения чисел в прямых кодах

Операция умножения состоит из ряда последовательных сложений. Сложением управляют разряды множителя: если в очередном разряде множителя содержится единица, то к сумме добавляется множимое. При этом, в зависимости от метода умножения, выполняется сдвиг либо множимого, либо частичной суммы. Наряду с этим умножение можно начинать как с младших, так и со старших разрядов множителя. Для умножения используют модули сомножителей. Знак произведения определяется сложением по модулю 2 знаковых разрядов сомножителей.

Введем некоторые обозначения, используемые ниже: 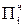- частичное произведение, 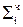- частичная сумма.

Ниже приводится схема четырех алгоритмов умножения (рис. 5).

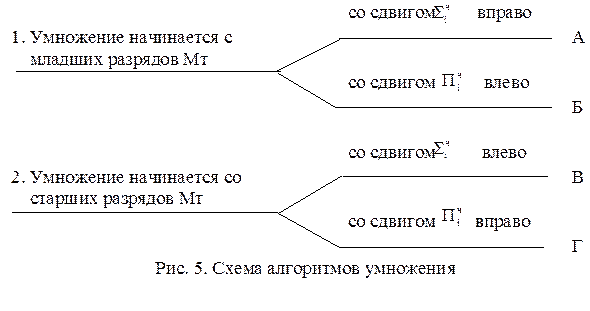
Остановимся более подробно на реализации умножения согласно алгоритму А.

Представим Мн = А = 0,а₁а₂…а_n

Мт = B = 0,b₁b₂….b_n = b₁2^-1+b₂2^-2+…+b_n2^-n+b_n2^-n

Мн∙Мт = С=А∙В= 0,а₁а₂…а_n ( b₁2^-1+b₂2^-2+…+b_n2^-n) =

= 0+(b₁∙0,а₁а₂…а_n)2^-1+…+(b_n-1∙0,а₁а₂…а_n)2^-(n-1)+(b_n∙0,а₁а₂…а_n)2^-n =

= 0+b₁∙A2^-1+…+b_n-1∙A2^-(n-1)+…+b_n∙A2^-n = 0+b_n∙A2^-n+b_n-1∙A2^-(n-1)+…+b₁∙A2^-1 =

= (…((0+b_n∙A)2^-1+b_n-1∙A)2^-1+…+b₁∙A)2^-1

Ниже приведены (без вывода) остальные три реализации алгоритмов (Б, В и Г) умножения.

Мн∙Мт = С=А∙В = 0+b_n∙A+b_n-1∙A∙2²+…+b₁∙A∙2^n-1 (алгоритм Б)

Мн∙Мт = С=А∙В = (…(0+b₁∙A) ∙2¹+b₂∙A)∙2¹+…+b_n∙A) (алгоритм В)

Мн∙Мт = С=А∙В = 0+b₁∙A∙2^-1+b₂∙A∙2^-2+…+b_n∙A∙2^-n (алгоритм Г)

Структурные схемы операционных устройств, выполняющих умножение по алгоритмам А, Б, В и Г, приведены на рис 6.

Рассмотрим пример умножения чисел согласно алгоритму А.

Пример: Мн = 0,1011

0,0000 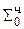начальное содержимое сумматора

⁺ 0,1011 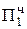= Мн ∙ b₄ первое частичное произведение

0,1011 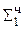первая частичная сумма

0,0101 1 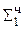∙ 2^-1 сдвиг первой частичной суммы

⁺ 0,0000 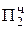= Мн ∙ b₃ второе частичное произведение

0,0101 1 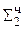вторая частичная сумма

0,0010 11 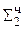∙ 2^-1 сдвиг второй частичной суммы

⁺ 0,1011 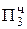= Мн ∙ b₂ третье частичное произведение

0,1101 11 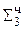третья частичная сумма

0,0110 111 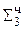∙ 2^-1 сдвиг третьей частичной суммы

⁺ 0,1011 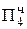= Мн ∙ b₁ четвертое частичное произведение

1,0001 111 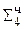(возникло переполнение)

0,1000 1111 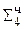∙ 2^-1 сдвиг, получение верного результа-

та Мн∙Мт

Заметим, что при умножении чисел по алгоритму А на отдельных этапах операции возможно переполнение (попадание значащей единицы в знаковый разряд). Однако при последующем сдвиге переполнение устраняется. При использовании других алгоритмов (Б, В, Г) переполнения не возникает.

Время умножения чисел по алгоритму А t_умн = ( t_сл + t_сдв ) n, где n - число разрядов Мт. Следовательно, сдвиг и сложение нельзя выполнять в одном автоматном такте. Это наглядно показано на рис 7.