Обоснование алгоритма адаптивной линейной интерполяции
Одним из наиболее эффективных методов устранения избыточности непрерывных сообщений, передаваемых по дискретным каналам, является адаптивная временная дискретизация (АВД). В процессе адаптивной дискретизации чаще всего реализуется один из апертурных методов сжатия данных, применяемый к непрерывному сигналу. В результате определяются моменты времени, в которые необходимо произвести выборки дискретных значений сигнала, а затем эти выборки (отсчеты) передаются по дискретному каналу. Если система передачи рассчитана на цифровые сигналы, то отсчеты подвергаются аналого-цифровому преобразованию. Эти операции могут быть совмещены. Устройство адаптивной дискретизации определяет моменты времени, когда нужно производить отсчеты, а АЦП производит преобразование сигнала в эти моменты.
Основу работы устройства АВД составляет контроль текущей погрешности аппроксимации сигнала выбранной аппроксимирующей функцией. Для этого используются различные методы оценки точности и приближенного факта нахождения сигнала в заданных границах. Если, например, сигнал аппроксимируется кусочно-линейной функцией, т.е. представляется на отрезках между отсчетами с помощью полинома первого порядка, то необходимо контролировать величину отклонения сигнала от такого полинома:
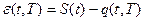
где:
e (t,T) — ошибка аппроксимации;
S(t) — сигнал;
q(t,T) — аппроксимирующая функция;
t — текущее время;
T — длина отрезка аппроксимации.
Если q(t,T) — интерполяционный полином первого порядка, то
при 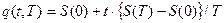 , ошибка
, ошибка 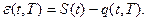
Для оценки величины ошибки аппроксимации 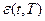 можно, например, использовать разложение сигнала в степенной ряд и анализировать остаточные члены этого ряда. Существует и множество других методов оценки, основанных на анализе дифференциальных или интегральных характеристик сигнала. Применительно к аналоговой реализации достаточно простыми и точными являются интегральные алгоритмы оценки погрешности аппроксимации. В общем случае эти алгоритмы не позволяют точно вычислять максимальное значение погрешности интерполяции
можно, например, использовать разложение сигнала в степенной ряд и анализировать остаточные члены этого ряда. Существует и множество других методов оценки, основанных на анализе дифференциальных или интегральных характеристик сигнала. Применительно к аналоговой реализации достаточно простыми и точными являются интегральные алгоритмы оценки погрешности аппроксимации. В общем случае эти алгоритмы не позволяют точно вычислять максимальное значение погрешности интерполяции 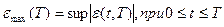 . Вместо величины
. Вместо величины 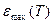 вычисляется некоторая функция, являющаяся ее оценкой например:
вычисляется некоторая функция, являющаяся ее оценкой например: 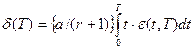
| |
Чтобы вычислять в явном виде 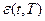 необходимо запоминать сигнал S(t) на всем отрезке [0,T], а это нежелательно. Поэтому необходимо заменить функцию под интегралом:
необходимо запоминать сигнал S(t) на всем отрезке [0,T], а это нежелательно. Поэтому необходимо заменить функцию под интегралом:
| |
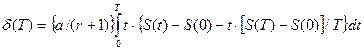
После интегрирования и замены 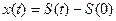 получим :
получим :
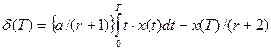 ;
;
| |
Величина постоянного коэффициента a принципиальной роли не играет, а определяет масштаб функции 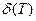 . Из практических сообра жений выбирают
. Из практических сообра жений выбирают 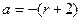 , тогда:
, тогда:
| |
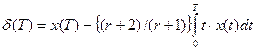
Если вычислять функцию 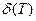 и контролировать ее величину таким образом, чтобы при выходе ее за пределы определенной зоны (апертуры ) производить отсчет значения сигнала, то можно осуществить адаптивную дискретизацию. При этом аппроксимация отсчетов с помощью кусочно-линейной интерполяции обеспечивает восстановление непрерывного сигнала с погрешностью, лежащей в пределах:
и контролировать ее величину таким образом, чтобы при выходе ее за пределы определенной зоны (апертуры ) производить отсчет значения сигнала, то можно осуществить адаптивную дискретизацию. При этом аппроксимация отсчетов с помощью кусочно-линейной интерполяции обеспечивает восстановление непрерывного сигнала с погрешностью, лежащей в пределах:
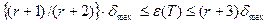
| |
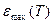 не должна превышать em, то величину
не должна превышать em, то величину 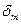 необходимо выбирать из соотношения:
необходимо выбирать из соотношения: 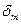 = e m / (r+3).
= e m / (r+3).
Таким образом, можно определить порог 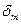 , который необходимо установить в реальном устройстве, осуществляющем адаптивную дискретизацию сигналов с погрешностью, не превышающей em.
, который необходимо установить в реальном устройстве, осуществляющем адаптивную дискретизацию сигналов с погрешностью, не превышающей em.
Необходимость автоматизации сбора и сжатия информации очевидна: даже при сравнительно небольших частотах опроса датчиков, тем более при большом количестве датчиков. Человек с этой задачей физически не сможет справиться.
Дата добавления: 2019-01-09; просмотров: 1171;
