Элементы теории кодирования

Большинство реальных сообщений обладают определенной избыточностью. При этом избыточность может быть естественной и искусственной (кодирование - процесс преобразования сообщения в комбинацию различных символов или соответствующим им сигналов). Естественная избыточность характерна для первичных алфавитов, а искусственная для вторичных. В свою очередь естественная подразделяется на семантическую и статистическую.

Семантическая - заключается в том, что мысль заключенная в сообщении, может быть сформулирована короче.

Статистическая избыточность обусловлена тем, что состояние элементов реальных сообщений неравномерны и взаимозависимы. При равновероятностных сообщениях, энтропия сообщений 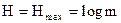, где m - количество сообщений. 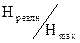характеризует, насколько данное реальное сообщение отличается от оптимального. Если количество информации реального и оптимального сообщения одинаковы, то 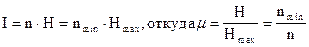- коэффициент сжатия.

Значит подходы к сжатию информации здесь - применение кодов, где Н максимальна.

- Устранение семантической избыточности

- Правильный учет статистических особенностей информационных посылок (вероятностное кодирование)

- Правильный выбор вторичного алфавита

- Оптимальное кодирование (Шеннона-Фано, Хаффмена)

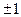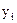Кодирование с преобразованием заключается в преобразовании множества взаимосвязанных сигналов в новую более независимую совокупность (Путем, например перемножения исходной совокупности на квадратную ортогональную матрицу А, элементами которой являются только . , если теперь произвести кодирование , то можно в ряде случаев существенно сократить избыточность).

При таком подходе к сигналу предъявляется единственное требование - достаточно низкая скорость изменения статистических свойств.

Этот подход обычно используется не изолированно, а в сочетании с разностными методами. Однако возможно и его самостоятельное использование. Здесь наиболее плодотворны методы, применяемые в теории распознавания образов и опирающиеся на теорию компактности образов.

Наконец, есть еще один подход к кодированию с уплотнением, основанный на изменении размерности, с помощью сохраняющего меру преобразования. Этот метод берет свое начало от идеи математика Кантора об отображении точек квадрата (т.е. площади) в точки на линии.

Разностная кодоимпульсная модуляция (РКИМ)

При реализации РКИМ входной процессор работает в режиме дифференциатора, сравнивающего текущее значение входного сигнала выборки 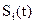со значением входного сигнала, которое было на предыдущем шаге, т.е. в момент времени 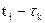. При этом в канал связи или процессор более высокого уровня вводится сигнал разности 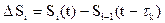, который, как правило, существенно меньше абсолютного значения входного сигнала. В качестве мгновенного значения коэффициента сжатия информации 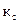здесь можно принять отношение 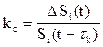и при переходе к относительно приведенным значениям (с усреднением на заданное число интервалов выборки N) .

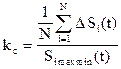Работа устройства РКИМ эффективна при частотах входных сигналов, не превышающих значения 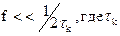- шаг квантования.

Разносная модуляция с экстраполяцией

РКИМЭ является развитием рассмотренной выше РКИМ. Здесь устройство также обеспечивает заданную последовательность выборок .Встроенный в устройство РКИМЭ экстраполятор осуществляет линейную оценку значений каждой из выборок, исходя из предшествующих ей выборок . Каждая из оценок вычитается из соответствующего значения выборки, в результате чего получается разностная последовательность или последовательность отключений .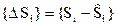

Полученные разности квантуются в квантователе в результате чего в сигнал добавляются шумы квантования . При этом в канал связи предается последовательность 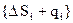. Коэффициент сжатия информации при использование РКИМЭ в принципе такой же, как и при РКИМ, но динамические характеристики несколько лучше.

Дельта модуляция (ДМ)

ДМ является частным случаем РКИМ, когда число разрядов передаваемой разности равно единице. В связи с ДМ - часто называют одноразрядной РКИМ. В связи с указанным возникает проблема так называемой перегрузке по крутизне, т.е. динамической ошибке, обусловленной тем, что при каждом шаге квантования передается лишь единичное приращение входной переменной. Для уменьшения динамической ошибки передаваемая крутизна (ПК) системы с ДМ должна быть больше крутизны входного сигнала, т.е. ,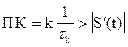

где k - значение приращения переменной на выходе,

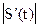- модуль производной входного сигнала по времени, 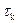- шаг квантования.

С точки зрения реализации система линейной ДМ является наиболее простой и надежной. Однако быстродействие таких систем относительно невелико. Различные системы нелинейной ДМ основаны на адаптивном изменении шага дискретизации, учете статистических свойств входных сигналов (кодирование в плоскости разряда).