Составляющую ошибки квантования – .

При равномерном квантовании шаг квантования 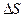– постоянный. Если процесс 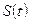стационарный, то шкала (динамический диапазон сигнала) 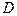для всех выборок одинакова, поэтому число уровней квантования 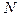не зависит от номера выборки: 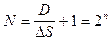, где – число разрядов бинарного кода .

Погрешность квантования является случайной функцией времени, вероятностные характеристики которых зависят от вероятностных характеристик процесса. В этом смысле погрешность квантования можно рассматривать как внешнюю аддитивную помеху 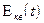(шум квантования). При малой допустимой погрешности квантования, когда 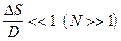шум квантования в различных выборках можно считать коррелированным, при этом можно ограничиться оценкой его одномерных вероятностных характеристик. Если началу шкалы соответствует уровень с номером 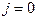, а концу шкалы уровень 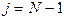и значение выборки отождествляется с ближайшим уровнем квантования или с серединой между соседними уровнями, то максимальная по модулю погрешность квантования:

; .

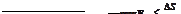
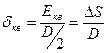При , как это обычно бывает на практике изменением плотности вероятности значений выборки на интервале, равном шагу квантования можно пренебречь и считать, что она распределена равномерно.

Тогда

s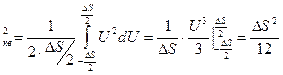

Откуда, считая сигнал нормально распределённым т.е.

s 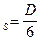(при равномерном распределении s )

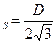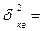
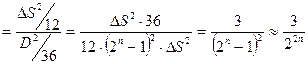
Откуда 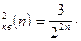s s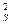

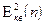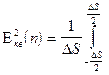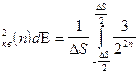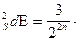Найдём , по определению: s s 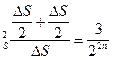s s ,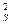

что и требовалось доказать.

Рассмотрим в выражении для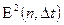

составляющую ошибки дискретизации –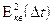

Рассматриваем как и в предыдущем случае пример равномерной дискретизации ( 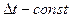) стационарного процесса 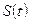с известной корреляционной функцией 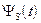. В качестве аппроксимирующей функции примем полином нулевой степени (ступенчатая интерполяция), при которой: , .

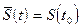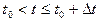В момент времени 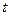текущая ошибка дискретизации равна:

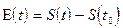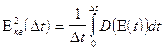; (1)

Дисперсия погрешности дискретизации при ступенчатой интерполяции выражается равенством 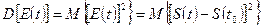. Раскрывая скобки и

учитывая, что у случайного стационарного эргодического процесса для случайной величины :

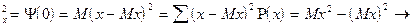
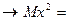s

s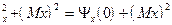

имеем:

,

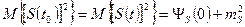
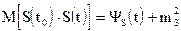где 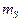– математическое ожидание 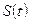, 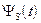– корреляционная функция для .

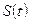Исходя из этого запишем формулу для 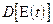в следующем виде:

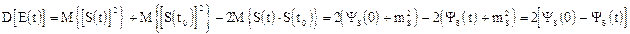
откуда из (1) и учитывая, что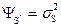

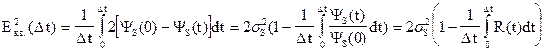
,где 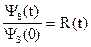- удельная корреляционная функция. Что и требовалось доказать.

Выражения для ошибок дискретизации и квантования для линейной интерполяции и критерия максимального отклонения, приведенные в таблице 1 здесь не доказываются, но при их определении используют подходы, аналогичные рассмотренным выше.