Апертурные алгоритмы, использующие экстраполяцию

Экстраполяционные методы прочно вошли в практику систем уплотнения информации, способствуя организации оптимального кодирования и селективной выборки, а так же обеспечивая реализацию в системах метода плавающей апертуры.

Задача экстраполяции может решаться по-разному, но всегда при одном условии — наличии некоторого известного свойства, связывающего прошлое процесса с его будущим, по крайней мере, в некотором статистическом смысле, для чего обычно требуется достаточно полное исследование предыстории процесса.

Альтернативой может служить (в случае управления инерционными объектами) возможность построения ускоренной адекватной математической или физической модели объекта.

Проще всего реализация прогнозирования достигается в случае детерминированных процессов, когда состояние процесса в любой будущий момент времени может быть точно предсказано по соответствующей информации о прошлом.

Наиболее широкое распространение получили экстраполяция нулевого порядка, линейная экстраполяция (первого порядка), а так же отчасти и экстраполяция второго порядка. Экстраполяция более высоких порядков неудобна для практического использования и почти никогда не применяется.

Значительно сложнее обстоит дело с прогнозированием недетерминированных процессов, т.к. здесь возникает дополнительная проблема минимизации неизвестной при экстраполяции ошибки. Теория экстраполяции стационарных случайных процессов была впервые развита в работах А. Н. Колмогорова и Н. Винера.

При экстраполировании очень важным является выбор шага (интервала) предсказания: чем меньше шаг, тем точнее прогноз. Не менее важным является и знание предыстории процесса : чем больше известно данных о предыдущих значениях, тем точнее подбираются коэффициенты экстраполяционного полинома. Однако приходится искать компромисс между точностью и простотой реализации.

В целом необходимо отметить, что экстраполятору, в основу работы которого заложено использование полинома Колмогорова, присущи черты, свойственные реальному дифференцирующему звену. Поэтому если в системе возможны высокочастотные помехи, более успешные результаты может дать прогнозирование, использующее методы экспоненциального сглаживания. В основе этих методов лежит предположение, что предсказываемое значение функции 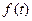может быть представлено в виде ряда Тейлора, причем члены ряда выражаются рекуррентными формулами экспоненциального сглаживания:

; ; …….

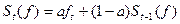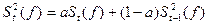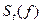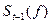где и — экспоненциально сглаженные значения первого порядка, характеризующие соответственно новое усредненное значение функции и предыдущее усредненное значение; 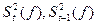— соответствующие экспоненциально сглаженные значения второго порядка и т.д.;

a — постоянный коэффициент, принимающий значения 0.5 < a < 1 для менее чувствительных систем, работающих в условиях сильных помех, 0.1 < a < 0.5 — для наиболее консервативных систем.

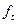— последнее измеренное значение функции.

При использовании всего двух членов ряда Тейлора, что в большинстве случаев вполне оправдано как с точки зрения точности, так и в смысле простоты физической реализации предикатора :

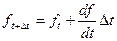, где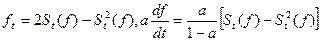

Большее число членов ряда использовать практически нецелесообразно из-за сложности вычислений и незначительного дополнительного выигрыша в точности прогнозирования.

Характеристика предикатора, реализующего алгоритм экспоненциального сглаживания, близка к характеристике предикатора Колмогорова, у которого на входе помещен сглаживающий фильтр.

Существуют другие экстраполяционные алгоритмы, однако они труднее реализуются и не имеют особых преимуществ перед описаными выше.