Выбор алгоритма классификации, обеспечивающего отнесение распознаваемого объекта или явления к соответствующему классу.

Построение алгоритма распознавания обеспечивает отнесение объекта к тому или иному классу на основании результатов измерения признаков. Алгоритмы строятся по-разному для детерминированных и для вероятностных признаков.

Алгоритмы принятия решения для систем распознавания, использующих детерминированные признаки, основываются на решении следующих задач.

1. Обосновывается выбор меры близости или сходства распознаваемого объекта 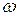с классами объектов 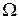. Эта мера носит название расстояния 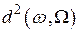между объектом 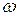и классом объектов .

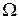2. Путем парных сравнений расстояний между распознаваемым объектом и всеми, указанными в классификации, классами объектов находится тот класс, расстояние до которого минимально.

Вновь введем следующие обозначения.

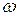- распознаваемый объект, измеренные значения признаков которого образуют вектор ,

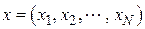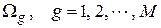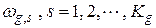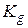- один из М классов. В этот класс входит некоторая совокупность эталонных объектов , где - число эталонных объектов в классе с номером g. Эталонными считаются объекты, по которым была проведена их классификация. В частном случае понятие объекта может совпадать с понятием класса.

Расстояние между объектом 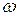и эталонным объектов 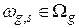, вычисляется чаще всего как сумма квадратов разностей между значениями их признаков:

,

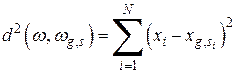где 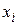и 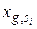- значения признаков объектов 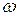и .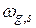

Среднее квадратическое (стандартное) расстояние между объектом и совокупностью эталонных объектов класса, то есть расстояние между объектом 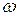и одним из классов объектов 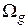, вычисляется как:

.

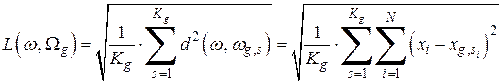Но различные признаки могут быть в разной степени важными для принятия решения. Для учета влияния существенности признака 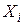вводится понятие веса признака 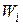. Веса должны выбираться так, чтобы их сумма равнялась единице .

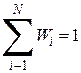С учетом весов признаков определяется среднее взвешенное расстояние между объектом распознавания 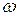и классом объектов :

.

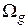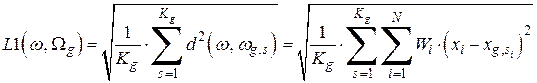Имея расстояния между объектом и классами объектов нужно теперь найти такой класс, расстояние до которого от распознаваемого объекта является наименьшим. Таким образом, принимается решение 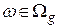, если

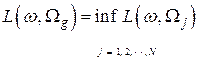
При работе с вероятностными признаками в процессе принятия решения следует учитывать вероятности ошибок первого и второго рода, связанные с ошибочным отнесением объекта не к тем классам, к которым они действительно принадлежат. Риски, связанные с ошибками при принятии решений, описываются платежной матрицей:

.

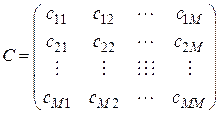Каждый элемент платежной матрицы 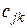- это потери, которые возникают в том случае, когда объект, в действительности относящийся к классу 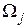, при распознавании мы ошибочно отнесем к классу 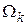. Очевидно, что в общем случае 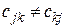. На главной диагонали стоят элементы, соответствующие безошибочным решениям. Эти потери или равны нулю, или они отрицательны. В последнем случае их можно трактовать как некоторый выигрыш. Элементы матрицы можно выражать в рублях, долларах, процентах. Построение матрицы – это результат совместной деятельности разработчиков системы и пользователей системы.

Мы уже говорили о том, что вероятностные признаки характеризуются

- условными плотностями распределения признаков:

,

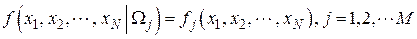- априорными вероятностями принадлежности объекта к тому или иному классу объектов:

.

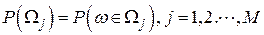Пусть в результате работы измерительной части системы распознавания получен вектор признаков объекта 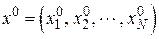. Обозначим это событие как 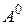. По результатам измерений вообще-то могут быть приняты разные решения 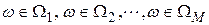, но с различными условными вероятностями 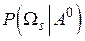. Эти вероятности отличаются от априорных вероятностей 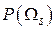принадлежности объекта к тому или иному классу и называются апостериорными вероятности принадлежности объекта к классу 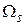. Различие между 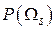и 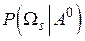обуславливается тем, что они получаются после предъявления системе распознаваемого объекта, при условии наступления события 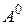. В идеальном случае все эти вероятности должны бы быть равными нулю кроме одной, относящейся к тому классу, к которому принадлежит распознаваемый объект. Но этого не получается по причине случайности распределения признаков по классам объектов. Апостериорные вероятности вычисляются по знаменитой формуле преподобного Байеса:

,

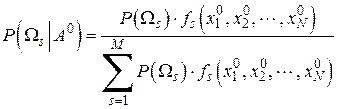где 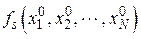- условные плотности распределения признаков 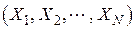при условии, что объект распознавания принадлежит классу 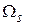, вычисленные в экспериментальных точках .

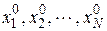Условный риск, связанный с принятием решения 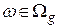при условии, что имело место событие 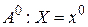, равен сумме рисков при принятии каждого решения, но умноженных на апостериорные вероятности принятия различных решений:

/

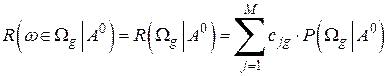Здесь 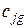- элементы платежной матрицы, соответствующие 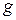-у столбцу платежной матрицы, то есть потери, связанные с тем, что объект, в действительности принадлежащий классу 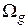, после получения результатов 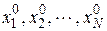будет отнесен к классам .

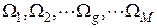Решение о принадлежности объекта к тому или иному классу принимается после вычисления всех этих рисков. Объект приписывается тому классу, для которого условный риск будет минимальным.

Для алгоритмов, основанных на логических признаках, понятие “мера близости” не имеет смысла. Здесь для принятия решения используются непосредственно булевы формулы, устанавливающие связь между классами и признаками. Эти формулы задаются для всех классов в виде:

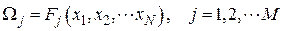
Если для какого-то объекта 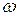при измерениях получен вектор признаков 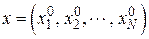и при этом 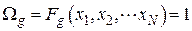, то принимается решение .

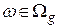Для примера рассмотрим примитивную систему распознавания болезней. Распознаванию подлежит два класса: 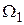- простуда (ОРЗ) и 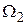- ангина. В качестве признаков используются следующие симптомы:

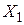- наличие повышенной температуры,

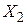- наличие насморка,

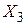- наличие нарывов в горле.

Каждый из признаков может принимать только два значения: 0 (ложь, отсутствие признака) и 1 (истина, наличие признака). Соотношения между признаками и классами задается булевой формулой:

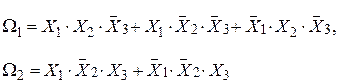
Пришел пациент. Измерительная часть системы распознавания определила вектор признаков: 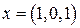, то есть температура повышена, однако насморка нет, а в горле имеются нарывы. Для принятия решения вычисляем булевы функции:

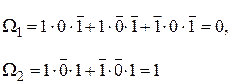
Приходится признать, что пациент болен ангиной.