Блок-схема алгоритма

Данный способ оказался очень удобным средством изобра­жения алгоритмов и получил широкое распространение в науч­ной и учебной литературе.

Структурная (блок-, граф-) схема алгоритма - графическое изображение алгоритма в виде схемы связанных между собой с помощью стрелок (линий перехода) блоков - графических сим­волов, каждый из которых соответствует одному шагу алгорит­ма. Внутри блока дается описание соответствующего действия.

Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, т.к. зрительное восприятие обычно облегчает процесс написа­ния программы, ее корректировки при возможных ошибках, ос­мысливание процесса обработки информации.

Можно встретить такое утверждение: «Внешне алгоритм представляет собой схему - набор символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации». Здесь форма представления алго­ритма смешивается с самим алгоритмом.

Принцип программирования «сверху вниз» требует, чтобы блок-схема поэтапно конкретизировалась и каждый блок «рас­писывался» до элементарных операций. Но такой подход можно осуществить при решении несложных задач. При решении сколь­ко-нибудь серьезной задачи блок-схема «расползется» до такой степени, что ее невозможно будет охватить одним взглядом.

Блок-схемы алгоритмов удобно использовать для объясне­ния работы уже готового алгоритма, при этом в качестве блоков берутся действительно блоки алгоритма, работа которых не тре­бует пояснений. Блок-схема алгоритма должна служить для уп­рощения изображения алгоритма, а не для усложнения. В табл. 2.1 приведены наиболее часто употребляемые сим­волы.

Таблица 2.1

Типовые обозначения структурной схемы

Название символа	Обозначение и пример заполнения	Пояснение
Процесс		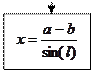Вычислительное действие или последовательность действия
Ветвление		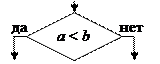Проверка условий
Модификация		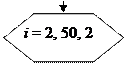Начало цикла
Предопределенный процесс		Вычисления по подпрограмме, стандартной подпрограмме
Ввод–вывод		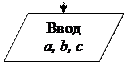Ввод-вывод в общем виде
Пуск–останов		Начало, конец алгоритма, вход и выход в подпрограмму
Документ		Вывод результатов на печать

Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения на­глядности схемы несколько отдельных блоков обработки мож­но объединять в один блок. Представление отдельных операций достаточно свободно.

Блок «ветвление» используется для обозначения переходов уп­равления по условию. В каждом блоке «ветвление» должны быть указаны вопрос, условие или сравнение, которые он определяет.

Блок «модификация» используется для организации цикли­ческих конструкций. (Слово модификация означает видоизме­нение, преобразование.) Внутри блока записывается параметр цикла, для которого указываются его начальное значение, гра­ничное условие и шаг изменения значения параметра для каж­дого повторения.

Блок «предопределенный процесс» используется для указа­ния обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.

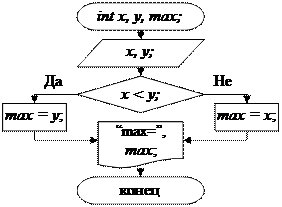Рис. 2.1. Блок-схема алгоритма нахождения максимального из двух значений

Псевдокод представляет собой систему обозначений и пра­вил, предназначенную для единообразной записи алгоритмов. Он занимает промежуточное место между естественным и фор­мальным языками. С одной стороны, он близок к обычному естественному язы­ку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде использу­ются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.

В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облег­чает запись алгоритма на стадии его проектирования и дает воз­можность использовать более широкий набор команд, рассчи­танный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формаль­ным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдо­коде, так же, как и в формальных языках, есть служебные сло­ва, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте под­черкиваются. Единого или формального определения псевдо­кода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.

Программное представление алгоритма. При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается определенный произвол при изоб­ражении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм. Однако на практике в качестве исполнителей алгоритмов ис­пользуются компьютеры, поэтому ал­горитм, предназначенный для исполнения на компьютере, дол­жен быть записан на «понятном» ему языке. И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполните­лем. Язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком програм­мирования, а запись алгоритма на этом языке - программой для компьютера.

Системы счисления

Системой счисления называется совокупность приемов наиме­нования и записи чисел.

В любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы исчисления. Символы, используемые для записи чисел, могут быть любыми, только они должны быть разными и значение каждого из них должно быть известно. В современном мире наиболее распространенным является представление чисел посредством арабских цифр 0, 1,2, 3, 4, 5, 6, 7, 8, 9 - специальных знаков, используемых для записи чисел. Системы счисления различаются выбором базисных чисел и правилами образования из них остальных чисел. Например, в римской системе счисления базисными являются числа 1, 5, 10, 50, 100, 500, 1000, которые обозначаются знаками I, V, X, L, С, D, М, а другие получаются путем сложения и вычитания базисных: если цифра справа меньше или равна цифре слева, то эти цифры складываются; если цифра слева меньше, чем цифра справа, то левая цифра вычитается из правой. Так, например, число 146 в римской системе счисления имеет вид CXLVI (С-100, XL-40, VI-6), здесь «сорок» получается посредством вычитания из «пятидесяти» числа «десять», «шесть» - посредством сложения «пяти» и «единицы». Системы счисления, в которых любое число получается путем сложения или вычитания базисных чисел, называются аддитивными. При таком представлении чисел правила сложения для небольших чисел очевидны и просты, однако если возникает необходимость выполнять операции сложения над большими числами или операции умножения и деления, то «римская» система счисления оказывается неудобной. В этой ситуации преимущественнее оказываются пози­ционные системы счисления. Хотя в них, как правило, представления чисел далеко не так просты и очевидны, как в «римской» системе счисления, систематичность представления, основанная на «пози­ционном весе» цифр, обеспечивает простоту выполнения операций умножения и деления.

В «римской» системе счисления каждый числовой знак в записи любого числа имеет одно и то же значение, т.е. значение числового знака не зависит от его расположения в записи числа. Таким образом, «римская» система счисления не является позиционной системой счисления.

Для изображения (или представления) чисел в настоящее время используются в основном позиционные системы счисления. При­вычной для всех является десятичная система счисления. В этой системе для записи любых чисел используется только десять разных знаков (цифр): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Эти цифры введены для обозначения первых десяти последовательных чисел, а следующее число 10 и т.д. обозначается уже без использования новых цифр. Однако введением этого обозначения сделан важный шаг в построении системы счисления: значение каждой цифры поставлено в зависимость от того места, где она стоит в изображении числа.

Таким образом, система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Десятичная позиционная система счисления основана на том, что десять единиц каждого разряда объединяются в одну единицу соседнего старшего разряда. Таким образом, каждый разряд имеет вес, равный степени 10. Например, в записи числа 343.32 цифра 3 повторена три раза, при этом самая левая цифра 3 означает количество сотен (ее вес равен 10²); цифра 3, стоящая перед точкой, означает количество единиц (ее вес равен 10⁰), а самая правая цифра 3 - количество десятых долей единицы (ее вес равен 10^-1), так что последовательность цифр 343.32 представляет собой сокращенную запись выражения :

3´10²+4´10¹+3´10⁰+3´10^-1+2´10^-2

Десятичная запись любого числа X в виде последовательности цифр:

a_na_n-1…a₁a₀a_-1…a_-m… (3.6)

основана на представлении этого числа в виде полинома:

X = a_n´10ⁿ + a_n-1´10^n-1+…+ a₁´10¹+ a₀´10⁰ + a_-1´10^-1+…+ a_-m´10^-m… (3.7)

где каждый коэффициент а_i, может быть одним из чисел, для обозначения которых введены специальные знаки. Запись числа X в виде (3.7) представляет собой просто перечисление всех коэффи­циентов этого полинома. Точка, отделяющая целую часть числа от дробной, служит для фиксации конкретных значений каждой позиции в этой последовательности цифр и является началом отсчета.

Число К единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления, а сама система счисления называется К-ичной. Например, основанием десятичной системы счисления является число 10; двоичной - число 2; троичной - число 3 и т.д. Для записи произвольного числа в K-ичной системе счисления достаточно иметь К разных цифр а_i, i=1,...,К. Эти цифры служат для обозначения некоторых различных целых чисел, называемых базисными.

Числа можно записать как суммы степеней не только числа 10, но и любого другого натурального числа, большего 1. Например, в Древнем Вавилоне использовалась система счисления с основанием 60. Деление часа на 60 минут, а минуты на 60 секунд заимствовано именно из этой системы счисления. А то, что человечество выбрало в качестве основания системы счисления число 10, вероятно, связано с тем, что природа наделила людей десятью пальцами.

Запись произвольного числа X в K-ичной позиционной системе счисления основывается на представлении этого числа в виде полинома:

K=a_nKⁿ + a_n-1K^n-1 +…+ a₁K¹ + a₀K⁰ + a_-1K^-1 +…+ a_-mK^-m +… (3.8)

где каждый коэффициент а, может быть одним из базисных чисел и изображается одной цифрой. Как и в десятичной системе счисления, число X, представленное в К-ичной системе счисления, можно кратко записать в виде (3.6) путем перечисления всех коэффициентов полинома (3.8) с указанием позиционной точки. Последовательность цифр, стоящая в (3.6), является изображением числа X в К-ичной системе счисления. Базисные числа должны быть выбраны так, чтобы любое число X могло быть представлено в виде полинома (3.8). Обычно в качестве базисных чисел берутся последовательные целые числа от 0 до К-1 включительно.

Все известные позиционные системы счисления являются адди­тивно-мультипликативными. Особенно отчетливо аддитивно-мультипликативный способ образования чисел из базисных выражен в числительных русского языка, например пятьсот шестьдесят восемь (т.е. пять сотен плюс шесть десятков плюс восемь).

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими полиномами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые имеют место при данном основании К системы счисления.

Отметим, что во всех позиционных системах счисления с любым основанием К умножения на числа вида К^m , где m - целое число, сводится просто к перенесению запятой у множимого на m разрядов вправо или влево (в зависимости от знака m), так же как и в десятичной системе.

Для указания того, в какой системе счисления записано число, условимся при его изображении основание системы счисления указывать в виде нижнего индекса при нем, например, 35.648.

В современной вычислительной технике, в устройствах авто­матики и связи широко используется двоичная система счисления. Это система счисления с наименьшим возможным основанием. В ней для изображения числа используются только две цифры: 0 и 1.

Произвольное число X в двоичной системе представляется в виде полинома:

X = a_n´2ⁿ + a_n-1´2^n-1+…+ a₁´2¹+ a₀´2⁰ + a_-1´2^-1+…+ a_-m´2^-m… (3.9)

где каждый коэффициент а_i может быть либо 0, либо 1.

Так как в двоичной системе счисления для изображения любых чисел используются только две различные цифры, то при построении ЭВМ можно использовать элементы, которые могут находиться только в двух состояниях (например, высокое или низкое напряжение в цепи, наличие или отсутствие электрического импульса и т.п.). Это обстоятельство, а также простота выполнения арифметических операций являются причиной того, что большинство современных ЭВМ используют двоичную систему счисления.

Неудобство использования двоичной системы счисления заключается в громоздкости записи чисел. Это неудобство не имеет существенного значения для ЭВМ. Однако если возникает необхо­димость кодировать информацию «вручную», например, при состав­лении программы на машинном языке, то предпочтительнее ока­зывается пользоваться восьмеричной или шестнадцатеричной сис­темой счисления (в силу их свойств, которые будут отмечены позднее).

В восьмеричной системе счисления базисными числами являются 0, 1, 2, 3, 4, 5, 6, 7. Запись любого числа в этой системе основывается на его разложении по степеням числа восемь с коэффициентами, являющимися указанными выше базисными числами.

Например, десятичное число 83.5 в восьмеричной системе будет
изображаться в виде 123.4. Действительно, эта запись по
определению означает представление числа в виде полинома:
1х8²+2х8¹+3х8⁰+4х8^-1 = 64 + 16 + 3 + 4/8 = 83.5.

В шестнадцатеричной системе счисления базисными являются числа от нуля до пятнадцати. Эта система отличается от рассмотренных ранее тем, что в ней общепринятых (арабских) цифр не хватает для обозначения всех базисных чисел, поэтому приходится вводить в употребление новые символы. Обычно для обозначения первых десяти целых чисел от нуля до девяти используют арабские цифры, а для следующих целых чисел от десяти до пятнадцати используются буквенные обозначения A, B, C, D, E, F.

Например, десятичное число 175.5 в шестнадцатеричной системе будет записываться в виде AF.8. Действительно:

Смешанные системы счисления

В ряде случаев числа, заданные в системе счисления с основанием Р, приходится изображать с помощью цифр другой системы счисления с основанием Q, где Q<P. Такая ситуация возникает, например, когда в ЭВМ, способной непосредственно воспринимать только двоичные числа, необходимо изобразить десятичные числа, с которыми мы привыкли работать. В этих случаях используются смешанные системы счисления, в которых каждый коэффициент Р-ичного разложения числа записывается в Q-ичной системе. В такой системе Р называется старшим основанием, a Q - младшим основанием, а сама смешанная система называется (Q - Р)-ичной. Для того чтобы запись числа в смешанной системе счисления была однозначной, для представления любой Р-ичной цифры отводится одно и то же количество Q-ичных разрядов, достаточное для предс­тавления любого базисного числа Р-ичной системы. Так, в сме­шанной двоично-десятичной системе счисления для изображения каждой десятичной цифры отводится четыре двоичных разряда. Например, десятичное число х = 925 в двоично-десятичной системе запишется в виде 1001 0010 0101. Здесь последовательные четверки (тетрады) двоичных разрядов изображают цифры 9, 2, 5 записи числа в десятичной системе счисления. Следует обратить внимание, что хотя в двоично-десятичной записи числа и используются только цифры 0 и 1, эта запись отличается от двоичного изображения данного числа. Например, приведенный выше двоичный код в двоичной системе счисления изображает число 2341, а не число 925.

Условимся изображать принадлежность числа к (Q - Р)-ичной системе счисления с помощью нижнего индекса (Q - Р) при данном числе, например: 925₁₀= 100100100101_2-10

Аналогично рассмотренной выше двоично-десятичной системе можно использовать и другие смешанные системы при различных значениях Р и Q. Особого внимания заслуживает случай, когда Р = Q^z, где z - целое положительное число. В этом случае запись какого-либо числа в смешанной системе тождественно совпадает с изображением этого числа в системе счисления с основанием Q (что не имеет места в двоично-десятичной системе в общем случае ).

Докажем это утверждение. Рассмотрим произвольное целое число N. В Р-ичной системе счисления это число будет записано в виде

p_np_n-1…p₁p₀,

основанном на представлении

N=p_npⁿ+p_n-1p^n-1+…+p₁p¹+p₀ (3.10)

где p_i, i = 0, 1, .... n являются базисными числами этой системы.

Каждый коэффициент p_i будет записываться в Q-ичной системе счисления в виде,

p_i = q_i,z-1 q_i,z-2 … q_i,z q_i,0

основанном на представлении

p_i = q_i,_z-1Q^z-1 + q_i,_z-2Q^z-2 +… + q_i,₁Q¹ + q_i,₀ (3.11)

где q_i,j - базисные числа системы счисления с основанием Q.

Тогда в смешанной системе счисления число N будет запи­сываться в виде

N = q_n,z-1 q_n,z-2 … q_n,0 q_n-1,z-1 … q_n-1,0 …q_0,z-1… q_0,0

Подставляя (3.11) в (3.10) и учитывая соотношение Р = Q^z , получим

N = q_n,_z-1Q^nz+z-1 + q_n,_z-2Q^nz+z-2 +…+ q_n,₀Q^nz + q_n-1,_z-1Q^nz-1 + q_n-1,₀Q^nz-1 +…+

+q₀,_z-1Q^nz-1 +…+ q₀,_z-1Q^z-1 +…+ q₀,₀Q⁰ (3.12)

т.е. разложение числа N по степеням Q. Поэтому запись числа N в Q-ичной системе счисления, соответствующая разложению (3.12), будет
иметь вид

N = q_n,z-1 q_n,z-2 … q_n,0 q_n-1,z-1 … q_n-1,0 …q_0,z-1… q_0,0 .

Как видно, эта запись тождественно совпадает с приведенной выше записью числа N в смешанной системе счисления, где каждая очередная группа из z цифр является просто изображением соответствующего коэффициента p_i, в системе счисления с осно­ванием Q.

Все сказанное выше относительно целых чисел автоматически переносится и на случай произвольных чисел. Таким образом, изображение числа x: в Р-ичной системе счисления в случае Р = Q^z является просто сокращенной записью изображения этого же числа х в Q-ичной системе .

Рассмотренное выше свойство некоторых смешанных систем широко используется на практике для сокращенной записи чисел, заданных в системе счисления с небольшим основанием. Для этого в исходной записи числа разряды объединяются вправо и влево от точки в группы некоторой длины (добавляя в случае необходимости левее старшей или правее младшей значащих цифр соответствующее количество нулей), и каждая такая группа записывается одной циф­рой другой системы, основание которой равно соответствующей степени исходного основания.

Перевод чисел из одной системы счисления в другую

При решении задач с помощью ЭВМ исходные данные обычно задаются в десятичной системе счисления; в этой же системе, как правило, нужно получить и окончательные результаты. Так как в современных ЭВМ данные кодируются в основном в двоичных кодах, то, в частности, возникает необходимость перевода чисел из десятичной в двоичную систему счисления и наоборот.

При рассмотрении правил перевода чисел из одной системы счисления в другую ограничимся только такими системами счис­ления, у которых базисными числами являются последовательные целые числа от 0 до Р-1 включительно, где Р - основание системы счисления.

Задача перевода заключается в следующем. Пусть известна запись числа х в системе счисления с каким-либо основанием Р:

p_np_n-1…p₁p₀p_-1p_-2…,

где р_i - цифры Р-ичной системы (0 £ р_i £ Р-1). Требуется найти запись этого же числа х в системе счисления с другим основанием Q:

q_sq_s-1…q₁q₀q_-1q_-2…,

где q_i - искомые цифры Q-ичной системы (0 £ q_i £ Q-1). При этом можно ограничиться случаем положительных чисел, так как перевод любого числа сводится к переводу его модуля и приписыванию числу нужного знака.

При рассмотрении правил перевода нужно учитывать, средствами какой арифметики должен быть осуществлен перевод, т.е. в какой системе счисления должны быть выполнены все необходимые для перевода действия. Условимся считать, что перевод должен осущест­вляться средствами Р-ичной арифметики.

Перевод Q®P. Задача перевода произвольного числа х, задан­ного в системе счисления с основанием Q, в систему счисления с основанием Р сводится к вычислению полинома вида

X=q_nQⁿ + q_n-1Q^n-1 +…+ q₁Q¹ + q₀Q⁰ + q_-1Q^-1 +…+ q_-mQ^-m (3.13)

Для получения Р-ичного изображения выражения (3.13) необхо­димо все цифры q_i и число Q заменить Р-ичными изображениями и выполнить арифметические операции в Р-ичной системе счисления.

Заметим, что при переводе следует придерживаться правила сохранения точности изображения числа в разных системах, причем под точностью понимается значение единицы самого младшего (правого) разряда, используемого в записи числа в той или иной системе счисления.

Перевод Р®Q. Так как для перевода любого числа достаточно уметь переводить его целую и дробную части, рассмотрим отдельно эти два случая.

1. Перевод целых чисел. Пусть известна запись целого числа N в системе счисления с основанием Р и требуется перевести это число в систему счисления с основанием Q. Так как N - целое, то его запись в Q-ичной системе счисления имеет вид

N = q_sq_s-1…q₁q₀,

где q_i - искомые цифры Q-ичной системы (0 £ q_i < Q-1). Для опреде­ления q₀ разделим обе части равенства:

N = q_sQ^s+ q_s-1Q^s-1+…+ q₁Q¹+q₀ (3.14)

на число Q, причем в левой части произведем деление, пользуясь
правилами Р-ичной арифметики (так как запись числа N в Р-ичной
системе счисления известна), а правую часть перепишем в виде

N/Q = q_sQ^s+ q_s-1Q^s-1+…+ q₁Q¹+q₀ / Q

Приравнивая между собой полученные целые и дробные части (учитывая, что q_i < Q):

[N/Q] = q_sQ^s-1+ q_s-1Q^s-2+…+ q₁

[N/Q]=q₀/Q

Таким образом, младший коэффициент q₀ в разложении (3.14) определяется соотношением

Q₀=Q[N/Q],

причем указанные здесь действия на самом деле не выполняются, так как q₀ является просто остатком от деления N на Q.

Положим

N₁=[N/Q]= q_sQ^s-1+ q_s-1Q^s-2+…+ q₁ .

Тогда N₁ будет целым числом и к нему можно применить ту же самую процедуру для определения следующего коэффициента q₁ и т.д.

Таким образом, при условии что N₀ = N, перевод чисел с использованием Р-ичной арифметики осуществляется по следующим рекуррентным формулам:

q_i = Q[N_i / Q], (3.15)

N_i+1 = [N_i / Q] (i=0, 1, 2).

Этот процесс продолжается до тех пор, пока не будет получено N_i+1=0.

Заметим, что поскольку все операции выполняются в системе счисления с основанием Р, то в этой же системе будут получены искомые коэффициенты qi, поэтому их необходимо записать одной Q-ичной цифрой.

2. Перевод дробных чисел. Пусть необходимо перевести в Q-ичную систему счисления правильную дробь х (0 < х < 1 ), заданную в Р-ичной системе счисления.

Так как х < 1, то число х в Q-ичной системе счисления можно представить в виде полинома

x = q_-1Q^-1 + q_-2Q^-2 + … + q_-m Q^-m +…, (3.16)

где q_-i (i = 1, 2, ...) - искомые коэффициенты Q-ичного разложения
числа х. Для определения q_-1 умножим обе части равенства (3.16) на
число Q, причем в левой части произведем умножение, пользуясь
правилами Р-ичной арифметики (так как запись числа x в Р-ичной
системе счисления известна), а правую часть перепишем в виде

xQ = q_-1 + q_-2Q^-1 + q_-mQ^-m+… .

Приравняем между собой полученные в правой части этого выражения целые и дробные части (учитывая, что 0 < q_i < Q):

[xQ]=q_-1 ,

[xQ]=q_-2Q^-1 + … + q_-mQ^-m+1 +…

Таким образом, младший коэффициент q_-1 в разложении (3.16) определяется соотношением

q_-1 = [x_iQ].

Положим

x₁ = [xQ] = q_-2Q^-1 +…+ q_-mQ^-m+1 +… .