Примеры решения задач. Рассчитайте значение константы Михаэлиса и значение максимальной скорости ( и ) всеми возможными методами для реакции гидролиза метилового эфира
Пример 1.
Рассчитайте значение константы Михаэлиса и значение максимальной скорости ( 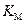 и
и  ) всеми возможными методами для реакции гидролиза метилового эфира N-бензоил-L-аминомасляной, катализируемого α-химотрипсином. Известны данные о зависимости начальной скорости от концентрации субстрата:
) всеми возможными методами для реакции гидролиза метилового эфира N-бензоил-L-аминомасляной, катализируемого α-химотрипсином. Известны данные о зависимости начальной скорости от концентрации субстрата:
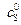 ·103, М ·103, М
| 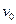 ·107, моль/с ·107, моль/с
|
| 2.24 | 4,25 |
| 2.24 | 4,31 |
| 1, 49 | 3,52 |
| 1, 49 | 3,60 |
| 1, 12 | 3,10 |
| 1, 12 | 3,12 |
| 0,90 | 2,71 |
| 0,90 | 2,77 |
| 0,75 | 2,45 |
| 0,75 | 2,40 |
Решение.
Для графического решения преобразуем уравнение Михаэлиса – Ментена в линейную форму.
1. Способ Лайнуивера – Берка.
Уравнение приводится к виду:
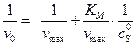
Рассчитанные значения 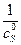 ,
, 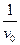 заносим в таблицу и строим график в соответствующих координатах.
заносим в таблицу и строим график в соответствующих координатах.
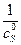 ∙10–2, М–1 ∙10–2, М–1
| 4,46 | 4,46 | 6,71 | 6,71 | 8,93 | 8,93 | 11,11 | 11,11 | 13,33 | 13,33 | |
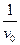 ∙10–6, с/моль ∙10–6, с/моль
| 2,35 | 2,32 | 2,84 | 2,78 | 3,23 | 3,21 | 3,69 | 3,61 | 4,08 | 4,17 | |
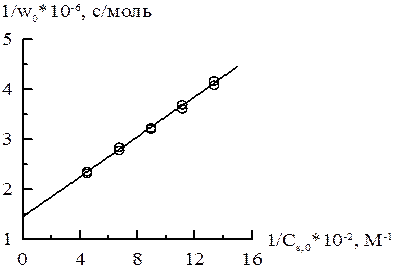
Отрезок на оси ординат получается равным 1/vmax = 1,45∙106, поэтому
vmax = 1 / (1,45∙106) = 6,9∙10–7 моль/с.
Тангенс угла наклона прямой равен tg α = 2000, следовательно
KМ = tg α ∙ vmax = 2000 ∙ 6,9∙10–7 = 1,38∙10–3 М.
2. Второй способ Лайнуивера – Берка
Строят график по уравнению
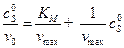
в координатах 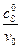 ,
, 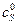
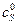 ∙103, М ∙103, М
| 2,24 | 2,24 | 1,49 | 1,49 | 1,12 | 1,12 | 0,90 | 0,90 | 0,75 | 0,75 |
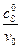 ∙10–3, с/моль ∙10–3, с/моль
| 5,27 | 5,20 | 4,23 | 4,14 | 3,61 | 3,59 | 3,32 | 3,25 | 3,06 | 3,13 |
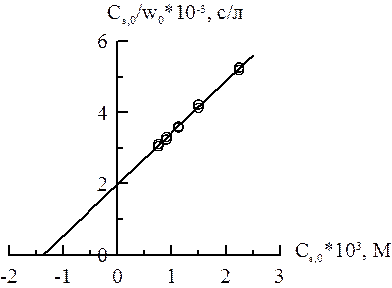
Из графика получается, что прямая отсекает на оси ординат отрезок, равный 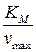 = 2∙103, а на оси абсцисс отрезок, равный – КМ = – 1,38∙10–3. Поэтому КМ = 1,38∙10–3 М, wmax = 1,38∙10–3/(2∙103) = 6,9∙10–7 моль/с.
= 2∙103, а на оси абсцисс отрезок, равный – КМ = – 1,38∙10–3. Поэтому КМ = 1,38∙10–3 М, wmax = 1,38∙10–3/(2∙103) = 6,9∙10–7 моль/с.
3. Способ Эдди–Хофсти.
Уравнение приводится к виду
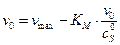
Строится график в координатах v0, 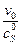 .
.
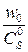 ∙104, л/с ∙104, л/с
| 1,90 | 1,92 | 2,36 | 2,42 | 2,77 | 2,79 | 3,01 | 3,08 | 3,27 | 3,20 |
| w0∙10–7, с/моль | 4,25 | 4,31 | 3,52 | 3,60 | 3,10 | 3,12 | 2,71 | 2,77 | 2,45 | 2,40 |
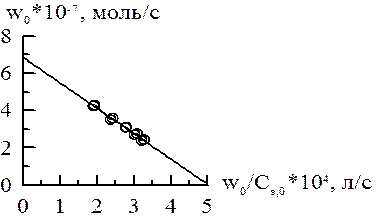
График даёт прямую линию, тангенс угла которой равен –1,36∙10–3, а отрезок, отсекаемый на оси ординат, равен 6,86∙10–3.
Поэтому. КМ = 1,36∙10–3 М, vmax = 6,86∙10–3 моль/с.
Пример 2.
Бензоат 1,2,5-триметилпиперидола-4 (β-изомер) ингибирует гидролиз бутирилхолина, катализируемый холинэстеразой. Определите тип ингибирования и рассчитайте константу диссоциации комплекса фермент–ингибитор. Экспериментальные данные:
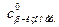 ·105, М ·105, М
| 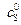 ·104, М ·104, М
| 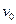 ·услов. Ед ·услов. Ед
|
| 10.00 2,50 0,91 0,50 | 5,55 4,45 2,94 2,09 | |
| 0,5 | 10.00 2,50 0,91 0,50 | 4,77 3,78 2,56 1,79 |
| 1,0 | 10.00 2,50 0,91 0,50 | 4,00 3,18 2,16 1,49 |
| 2,0 | 10.00 2,50 0,91 0,50 | 2,86 2,28 1,52 1,06 |
| 3,0 | 10.00 2,50 0,91 0,50 | 2,38 1, 58 1,24 0,87 |
Решение/
Рассчитаем константу Михаэлиса и максимальную скорость реакции для различных концентраций ингибитора по способу Эдди–Хофсти. Так как неизвестен способ ингибирования, то используем эффективные значения константы Михаэлиса и максимальной скорости Уравнение Михаэлиса–Ментена приведём к виду (по способу Эдди–Хофсти)
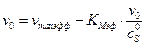
Построим графики зависимостей в координатах (v, 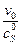 ) для разных значений концентрации ингибитора.
) для разных значений концентрации ингибитора.
Для 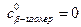 :
:
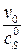 ∙10–4, усл.ед./М ∙10–4, усл.ед./М
| 0,56 | 1,78 | 3,23 | 4,18 |
| v0, усл.ед. | 5,55 | 4,45 | 2,94 | 2,09 |
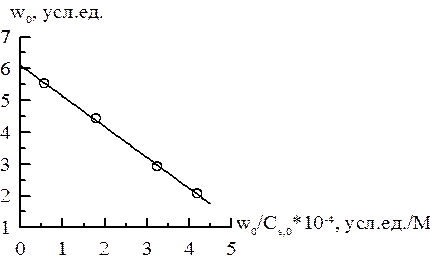
Уравнение прямой имеет вид 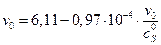 , поэтому получаем vmax = 6.11 у.е., KM = 0,97∙10–4 М.
, поэтому получаем vmax = 6.11 у.е., KM = 0,97∙10–4 М.
Для 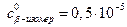 М:
М:
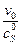 ∙10–4, усл.ед./М ∙10–4, усл.ед./М
| 0,48 | 1,51 | 2,81 | 3,58 |
| v0, усл.ед. | 4,77 | 3,78 | 2,56 | 1,79 |
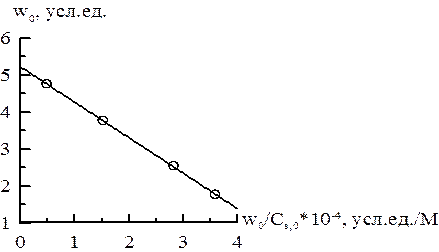
Уравнение прямой 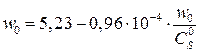 =>
=>
vmax эф.= 5,23 у.е., KMэф = 0,96∙10–4 М.
Для 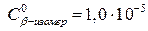 М:
М:
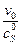 ∙10–4, усл.ед./М ∙10–4, усл.ед./М
| 0,40 | 1,27 | 2,37 | 2,98 |
| v0, усл.ед. | 4,00 | 3,18 | 2,16 | 1,49 |
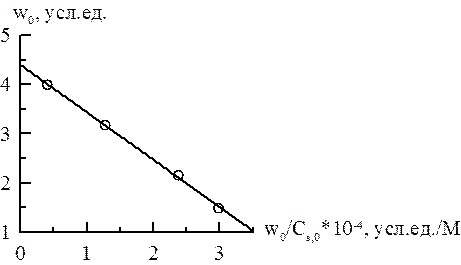
Уравнение прямой 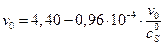 =>
=>
vmax эф = 4,40 у.е., KMэф = 0,96∙10–4 М.
Для 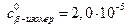 М:
М:
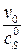 ∙10–4, усл.ед./М ∙10–4, усл.ед./М
| 0,29 | 0,91 | 0,67 | 2,12 |
| v0, усл.ед. | 2,86 | 2,28 | 1,52 | 1,06 |
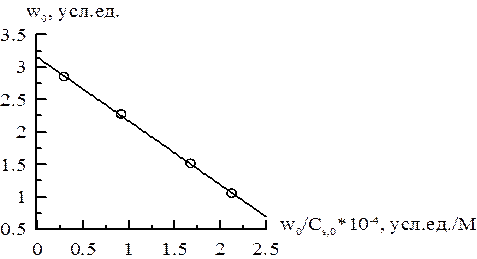
Уравнение прямой 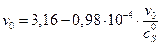 =>
=>
vmax эф = 3,16 у.е., KMэф = 0,98∙10–4 М.
Для 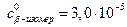 М:
М:
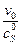 ∙10–4, усл.ед./М ∙10–4, усл.ед./М
| 0,24 | 0,63 | 1,36 | 1,74 |
| v0, усл.ед. | 2,38 | 1,58 | 1,24 | 0,87 |
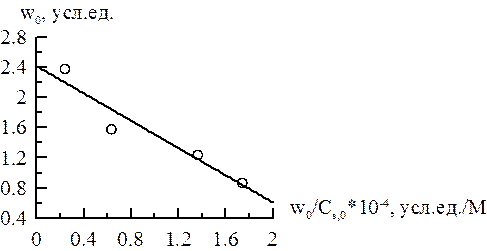
Уравнение прямой 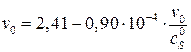 =>
=>
vmax эф = 2,41 у.е., KMэф = 0,90∙10–4 М.
Как видно из полученных значений, константа Михаэлиса остаётся неизменной, а максимальная скорость меняется. На этом основании можно сделать вывод, что ингибирование неконкурентное.
Рассчитываем константу ингибирования для 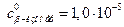 М по уравнению
М по уравнению
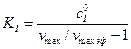
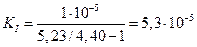 М.
М.
Вопросы для самоконтроля
1. Какие соединения получили название «ферменты»? Какова их природа?
2. Перечислите основные классы, на которые разделяются ферменты. Почему их классифицируют не по типу химического строения?
3. Какие вещества называются ингибиторами? Какие различают типы ингибиторов?
4. В каком случае ингибитор называется конкурентным? Укажите схематически механизм этого процесса.
5. Какие три графических способа существуют для определения постоянных 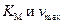 ?
?
6. Покажите как на основании опытных данных в отсутствие и в присутствии ингибитора определить константы: 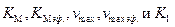 ?
?
Дата добавления: 2016-01-09; просмотров: 10718;
