Кинетика ферментативных реакций
Рассмотрим самую простую реакцию превращения субстрата (S) в продукт (Р) при участии фермента (Е).
Уже в ранних работах было обнаружено, что начальная скорость ферментативной реакции при фиксированной концентрации фермента и малых концентрациях субстрата изменяется линейно с концентрацией субстрата, но для высоких концентраций субстрата скорость реакции уже не зависит от концентрации субстрата.
Л. Анри (1903 г.) первым предложил идею, что фермент образует с субстратом промежуточный комплекс. Развил эту идею Л. Михаэлис.
Согласно этой идеи, механизм процесса можно представить состоящим из двух стадий. Первая обратимая и быстрая, вторая – необратимая и медленная:
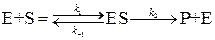
Для данного механизма скорость реакции определяется скоростью образования продукта реакции Р:
v 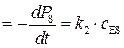 . (5.36)
. (5.36)
Скорость образования промежуточного продукта ES, равна:
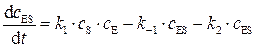 . (5.37)
. (5.37)
Уравнения материального баланса для фермента и субстрата имеют вид:
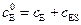 и
и 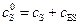 , (5.38)
, (5.38)
где 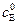 и
и 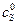 – начальные концентрации фермента и субстрата,
– начальные концентрации фермента и субстрата,  и
и 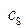 – их текущие концентрации,
– их текущие концентрации, 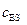 –концентрации промежуточного соединения и продукта реакции.
–концентрации промежуточного соединения и продукта реакции.
Решение системы из трех уравнений(5.36 – 5.38) находим из следующих условий:
1) для 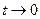 ,
, 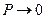 , следовательно,
, следовательно, 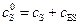 ;
;
2) обычно 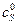 >>
>> 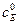 (или
(или 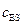 ) , поэтому
) , поэтому  ;
;
3) считают, что концентрация промежуточного соединения 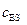 стационарна (на основе принципа стационарности Боденштейна), т.е.
стационарна (на основе принципа стационарности Боденштейна), т.е. 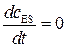 .
.
Подставляя значение 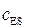 из (5.38) в (5.36) и решая его относительно
из (5.38) в (5.36) и решая его относительно 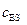 при условии
при условии 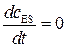 , получим
, получим
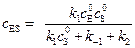 . (5.39)
. (5.39)
Поделим числитель и знаменатель этого уравнения на 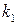 , тогда имеем:
, тогда имеем:
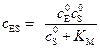 . (5.40)
. (5.40)
Величину  принято называть константой Михаэлиса.
принято называть константой Михаэлиса.
Подставляя уравнение (5.40) в (5.36), получим уравнение для скорости образования продукта в начальный момент времени:
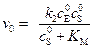 . (5.41)
. (5.41)
Анализ уравнения (5.41) позволяет объяснить наблюдаемые на опыте закономерности:
1) если КМ>> 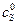 , тогда
, тогда
 , (5.42)
, (5.42)
то есть начальная скорость линейно зависит от концентрации субстрата. Этот факт полностью подтверждается экспериментальными данными;
2) если 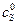 >>КМ, тогда из уравнения (5.41) получаем
>>КМ, тогда из уравнения (5.41) получаем
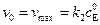 , (5.43)
, (5.43)
то есть начальная скорость не зависит от концентрации субстрата, что так же соответствует опытным данным. Следовательно, порядок реакции по субстрату в этом случае будет нулевой, а скорость процесса достигает максимального значения. Поэтому уравнение (5.41) можно записать в виде:
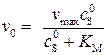 . (5.44)
. (5.44)
Уравнение (6.44) в литературе известно как уравнение Михаэлиса – Ментена. КМ называется константой Михаэлиса, физический смысл которой можно сформулировать, анализируя уравнение (5.44).
Константа Михаэлиса численно равна концентрации субстрата ( 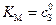 ), при которой активность фермента составляет половину максимальной, т.е.
), при которой активность фермента составляет половину максимальной, т.е. 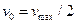 . Константой Михаэлиса имеет размерность концентрации, моль/л. Численные значения КМ обычно лежат в пределах 10-2 – 10-8 М, легко воспроизводятся и не зависят от концентрации фермента. В то же время КМ является функцией температуры, рН среды, зависит от присутствия других веществ, играющих роль ингибитора или активатора.
. Константой Михаэлиса имеет размерность концентрации, моль/л. Численные значения КМ обычно лежат в пределах 10-2 – 10-8 М, легко воспроизводятся и не зависят от концентрации фермента. В то же время КМ является функцией температуры, рН среды, зависит от присутствия других веществ, играющих роль ингибитора или активатора.
Если для рассматриваемого механизма реакции выполняется условие: 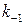 >>
>>  , тогда
, тогда 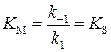 , где
, где 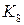 - субстратная константа, т.е. константа диссоциации фермент–субстратного комплекса на фермент и субстрат, характеризующая меру связывания фермента с субстратом. В общем случае
- субстратная константа, т.е. константа диссоциации фермент–субстратного комплекса на фермент и субстрат, характеризующая меру связывания фермента с субстратом. В общем случае 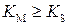 , причем экспериментальное значение
, причем экспериментальное значение 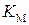 представляет собой максимальное значение
представляет собой максимальное значение 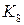 .
.
Только для ферментов разложения пероксида водорода, каталазы и пероксидазы, для которых 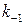 <<
<<  , константа Михаэлиса
, константа Михаэлиса 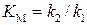 сильно отличается от субстратной константы
сильно отличается от субстратной константы 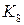 .
.
Величину  (размерность t-1) называют также числом оборотов фермента, так как она указывает на число моль субстрата, превращенных в продукт одним молем фермента в единицу времени. Для сложных реакций константу
(размерность t-1) называют также числом оборотов фермента, так как она указывает на число моль субстрата, превращенных в продукт одним молем фермента в единицу времени. Для сложных реакций константу  в уравнении Михаэлиса – Ментена обычно заменяют на
в уравнении Михаэлиса – Ментена обычно заменяют на 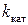 – каталитическую константу с той же размерностью.
– каталитическую константу с той же размерностью.
Для определения параметров 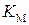 и
и  используют несколько способов лионеризации уравнения Михаэлиса – Ментена.
используют несколько способов лионеризации уравнения Михаэлиса – Ментена.
1. Первый способ (способ Лайнуивера – Берка).
Уравнение (5.44) приводят к виду:
 . (5.45)
. (5.45)
График прямой, построенной в координатах 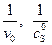 , отсекает отрезок на оси ординат, равный
, отсекает отрезок на оси ординат, равный 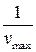 . Тангенс угла наклона прямой равен
. Тангенс угла наклона прямой равен 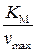 . Как следует из уравнения (5.45), константу
. Как следует из уравнения (5.45), константу 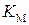 можно определить по отрезку, отсекаемому прямой на оси абсцисс, так как при
можно определить по отрезку, отсекаемому прямой на оси абсцисс, так как при 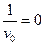 имеем соотношение:
имеем соотношение:
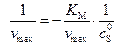 , (5.46)
, (5.46)
откуда 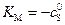 .
.
2. Второй способ (вторая форма уравнения Лайнуивера – Берка).
Уравнение (5.45) умножают на 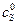 :
:
 . (5.47)
. (5.47)
График в координатах 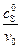 ,
, 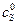 представляет собой также прямую, отсекающую на оси ординат отрезок, равный
представляет собой также прямую, отсекающую на оси ординат отрезок, равный 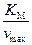 , а на оси абсцисс отрезок, равный –
, а на оси абсцисс отрезок, равный – 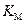 .
.
3. Третий способ (способ Эдди - Хофсти).
Если умножить обе части уравнения (5.45) на ( 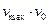 ), то оно приводится к виду:
), то оно приводится к виду:
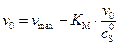 . (5.48)
. (5.48)
График, построенный в координатах ( 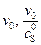 ), дает прямую линию, тангенс угла наклона которой равен
), дает прямую линию, тангенс угла наклона которой равен 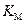 , а отрезок, отсекаемый на оси ординат равен
, а отрезок, отсекаемый на оси ординат равен 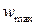 . Кроме того, как видно из рис. 2, отрезок, отсекаемый на оси абсцисс равен
. Кроме того, как видно из рис. 2, отрезок, отсекаемый на оси абсцисс равен 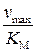 , так как при
, так как при 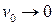
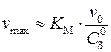 или
или  .
.
Указанные способы лианиризации уравнения Михаэлиса – Ментена охватывают различные области концентрации субстрата, когда возможны отклонения от линейности. Поэтому полезно значения 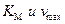 , определенные различными способами, сравнивать между собой.
, определенные различными способами, сравнивать между собой.
Нетрудно показать, что аналогичная (5.45) форма уравнения может быть получена и для более сложных механизмов реакции. Например, когда субстрат взаимодействует с ферментом по схеме:
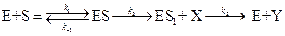 .
.
Выражение для начальной скорости в этом случае имеет вид:
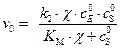 , (5.49)
, (5.49)
где 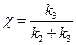 . Это уравнение аналогично по форме уравнению Михаэлиса – Ментена и также легко линеаризуется.
. Это уравнение аналогично по форме уравнению Михаэлиса – Ментена и также легко линеаризуется.
Возможно протекание более сложных ферментативных реакций с участием двух субстратов.
Дата добавления: 2016-01-09; просмотров: 1140;
