Влияние ингибиторов на кинетику ферментативных реакций
Вещества, присутствие которых в системе понижает активность фермента, то есть уменьшает скорость реакции, называются ингибиторами.
Эффект ингибирования может происходить по разным причинам.
1. Ингибитор I конкурирует с субстратом за активный центр, так как по строению близок к нему и является псевдосупстратом, образуя с ферментом неактивный комплекс:
Е + I=ЕI.
Константа диссоциации комплекса ЕI называется константой ингибирования:
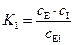 .
.
Начальная скорость реакции в присутствии ингибитора всегда меньше, чем в его отсутствие.
Если при увеличении концентрации субстрата в растворе активность фермента восстанавливается, такое ингибирование называется конкурентным.
Предельное значение скорости не зависит от присутствия ингибитора:
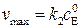 . (5.50)
. (5.50)
Уравнение Михаэлиса – Ментена в присутствии ингибитора в этом случае имеет вид:
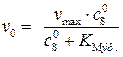 , (5.51)
, (5.51)
где
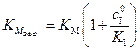 , (5.52)
, (5.52)
эффективная константа, зависящая от 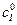 и
и 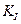 .
.
Если 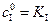 и
и 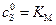 , то скорость реакции ингибирования будет равна
, то скорость реакции ингибирования будет равна 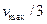 .
.
Выражение для константы ингибирования выразим из (5.52):
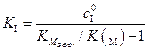 . (5.53)
. (5.53)
Таким образом, для определения КI , кроме 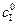 ,необходимо знать эффективную константу реакции в присутствии ингибитора и константу Михаэлиса в его отсутствие.
,необходимо знать эффективную константу реакции в присутствии ингибитора и константу Михаэлиса в его отсутствие. 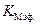 и
и 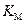 можно найти, решая задачу графическим методом, например в координатах Лайнуивера – Берга (
можно найти, решая задачу графическим методом, например в координатах Лайнуивера – Берга ( 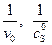 ) для случая процесса с ингибитором и без ингибитора. Константу ингибирования можно рассчитать по уравнению (5.53) или определить непосредственно из графика, так как отношение тангенсов угла наклона прямых в точке пересечения с осью ординат равно
) для случая процесса с ингибитором и без ингибитора. Константу ингибирования можно рассчитать по уравнению (5.53) или определить непосредственно из графика, так как отношение тангенсов угла наклона прямых в точке пересечения с осью ординат равно 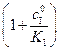 .
.
2. Ингибитор не конкурирует с субстратом за активный центр, так как присоединяется к другой части молекулы белка с образованием неактивных комплексов (EI и ESI), имеющих константы равновесия:
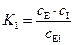
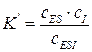 (5.54)
(5.54)
Наличие ингибитора в этом случае приводит к снижению активности фермента, но не изменяет его сродство к субстрату.
Если достигается обратимость ингибирования, то есть восстановление активности фермента под действием отличных от субстрата веществ, такое ингибирование называется неконкурентным.
Если оба комплекса (EI и ESI) неактивны, то есть не дают продукта, а константы их диссоциации близки между собой ( 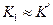 ), то это равносильно дополнительному условию: ингибитор не мешает взаимодействию субстрата с ферментом, но уменьшает скорость реакции из-за неактивности образующихся комплексов на поверхности фермента.
), то это равносильно дополнительному условию: ингибитор не мешает взаимодействию субстрата с ферментом, но уменьшает скорость реакции из-за неактивности образующихся комплексов на поверхности фермента.
В этом случае константа Михаэлиса остается постоянной величиной, а изменяется максимальная скорость процесса:
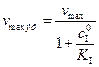 (5.55)
(5.55)
Уравнение Михаэлиса – Ментена в этом случае запишется как
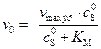 . (5.56)
. (5.56)
Если 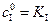 и
и 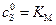 , то скорость реакции ингибирования будет равна
, то скорость реакции ингибирования будет равна 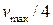 .
.
Выражение для константы ингибирования получим из (5.55):
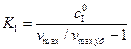 . (5.57)
. (5.57)
Линеаризация уравнения (5.56) и обработка экспериментальных данных для неконкурентного ингибирования в координатах 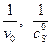 позволяет определить
позволяет определить 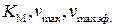 и
и 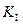 зная
зная 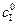 .
.
3. При бесконкурентном ингибировании образуется один не активированный комплекс (ESI) с константой равновесия
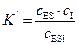 . (5.58)
. (5.58)
Уравнение Михаэлиса – Ментена в этом случае запишется как
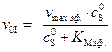 , (5.59)
, (5.59)
где
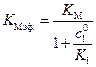 . (5.60)
. (5.60)
В этом случае эффективная константа отличается от значения для конкурентного ингибирования, но эффективная скорость выражается уравнением, аналогичным для не конкурентного ингибирования.
Линеаризация уравнения (5.59) и обработка экспериментальных данных для неконкурентного ингибирования в координатах 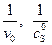 позволяет определить постоянные
позволяет определить постоянные 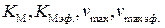 и
и 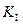 зная cI0.
зная cI0.
Дата добавления: 2016-01-09; просмотров: 2032;
