ТЕЧЕНИЕ НЬЮТОНОВСКОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ

Рассмотрим ламинарное течение вязкой (ньютоновской) жидкости в круглой трубе радиуса R. При таком течении цилиндрические слои жидкости (которые должны мыслиться бесконечно тонкими) перемещаются в направлении оси трубы z, совершая "телескопическое" движение (рис. 8.2, а). Так как жидкость несжимаема, то скорость v остается постоянной по длине трубы и зависит только от расстояния r до центральной оси. Для определения зависимости 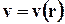составим уравнение равновесия сил, действующих на цилиндрический объем жидкости длиной l и радиусом r(рис. 8.3, б).

Сила вязкого сопротивления, действующая на внешнюю поверхность цилиндра со стороны внешних слоев, равна 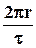. Эта сила уравновешивается раз­ницей сил давления, действующих на основания цилиндра, поэтому

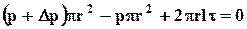,откуда 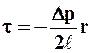(8.2.1)

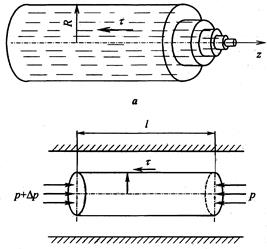Рис. 8.2. Ламинарное течение ньютоновской жидкости в трубе

(знак "минус" означает, что сила сопротивления направлена против оси z). По закону Ньютона

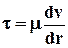, откуда

.

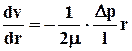Интегрируя это уравнение, получаем с учетом граничного усло­вия v (R) = 0 зависимость

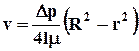. (8.2.2)

Измеряемой в опытах величиной является расход Q -объем жидкости, протекающей через поперечное сечение трубы за единицу времени, поэтому вычислим эту величину. Для этого разобьем сечение трубы на узкие кольца шириной dr. Расход жидкости через кольцо с внутренним диаметром г равен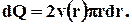

Расход через всё сечение может быть получен простым интегрированием:

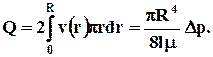(8.2.3)

Таким образом, в случае ньютоновской жидкости наблюдается линейная связь между перепадом давления и расходом жидкости.

Определив среднюю по сечению скорость V_ср -как 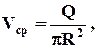получим отсюда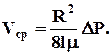

Распределение (8.2.2) было получено Стоксом (Stokes, 1849 г.) и Гагенбахом (Hagenbach, 1860 г.). Последний назвал соотношение 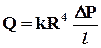законом Пуазейля в честь французского ученого (Poiseuille, 1797-1869), который в экспериментах с водой установил эмпирическую зависимость между расходом, геометрическими размерами тела и давлением.