ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОСТЕЙ В КОЛЬЦЕВОМ КАНАЛЕ
1. Для ньютоновской жидкости, используя соотношение для скорости деформации и напряжения сдвига (10.1.1) в системе уравнений (1.85), получаем простейшее уравнение состояния 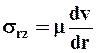 .
.
Сравнивая с решением (10.1.4), получаем для скорости:
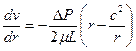 .
.
Решая это дифференциальное уравнение при граничных условиях v(aR) = v(R) = 0, получаем:
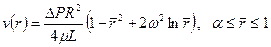 , (10.3.1)
, (10.3.1)
где aR и R (0 £ a £ 1) - радиусы внутреннего и внешнего цилиндров, ограничивающих кольцевой канал.
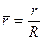 ,
, 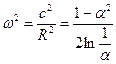 . (10.3.2)
. (10.3.2)
Скорость жидкости будет максимальной при 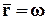 , а максимальные характеристики потока при этом будут:
, а максимальные характеристики потока при этом будут:
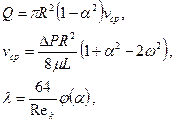 (10.3.3)
(10.3.3)
где 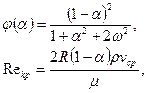
Reкр - параметр Рейнольдса для кольцевого канала.
При a > 0.3 j » 1.5 и поэтому l » 96/Reкр.
Кольцевой цилиндрический канал с соотношением радиусов окружностей сечения a > 0.3 и плоская щель с параметрами сечения 2h = R(1-a) b = pR(1+a) эквивалентны по интегральным гидродинамическим характеристикам при ламинарном течении ньютоновской жидкости ( средняя скорость, расход, коэффициент трения, перепад давления). Переход от ламинарного режима течения к турбулентному в кольцевом пространстве наступает быстрее, чем в плоской щели, так как 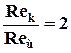 . При a = 0 (w = 0, j = 0) из формул (5.21) - (5.23) получаются известные формулы Гагена - Пуазейля, характеризующие течение жидкости в круглой трубе:
. При a = 0 (w = 0, j = 0) из формул (5.21) - (5.23) получаются известные формулы Гагена - Пуазейля, характеризующие течение жидкости в круглой трубе:
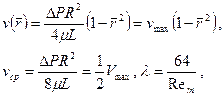
где 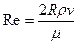 - параметр Рейнольдса для трубы.
- параметр Рейнольдса для трубы.
2. Для ньютоновской жидкости Шведова- Бингама течение в кольцевом канале возможно лишь при соблюдении условия
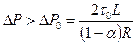 .
.
Аналитического решения этой задачи нет, возможно только численное. В результате сравнения с решением для кольцевого цилиндрического канала делается полезный вывод о том, что при течении жидкости Шведова - Бингама имеет место гидравлическая эквивалентность кольцевого цилиндрического канала и плоской щели, если DР>2DP0: a > 0.3; 2h=R(1-a); b = pR(1- a); t¢0/t0 =4/3j1 = 1.16 ¸ 1.17, где t¢0 и t0 - соответственно предельные напряжения сдвига для жидкостей в щелевом и кольцевом каналах.
Если принять j1 = ¾, т.е. h* = h(1 + 1/8 Sen), то последнее требование опускается. Аналогично первой задаче требование 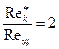 .
.
3. Для неньютоновской жидкости Освальда-Вейля задача решена только численно.
В предельном случае, когда R ® 0 (a = 0, w = 0, R2 = R), для распределения скорости в сечении круглой трубы имеем
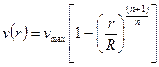 ,
,
где 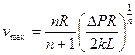 .
.
При этом основные интегральные характеристики потока жидкости в трубе принимают вид
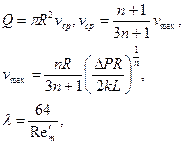
где 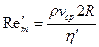 - обобщённый параметр Рейнольдса,
- обобщённый параметр Рейнольдса,
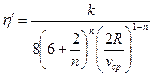 - приведённая вязкость жидкости для трубы.
- приведённая вязкость жидкости для трубы.
4. При турбулентном режиме течениязакон сопротивления слабо зависит от формы канала (круглая труба, кольцевое пространство, щель). В диапазоне чисел Рейнольдса 2 103 < Re k £ 105 коэффициент сопротивления рассчитывается по формуле Блазиуса 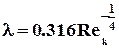 .
.
Дата добавления: 2016-01-09; просмотров: 2178;
