ДВИЖЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ В ПОРИСТОЙ СРЕДЕ
ОСНОВНЫЕ ПОНЯТИЯ
Грунт, вследствие неплотного прилегания образующих его частиц друг к другу, является пористой средой. Течение жидкости и газа (фильтрация) происходит в капиллярных каналах весьма сложной формы, образованных порами грунта. При решении вопросов фильтрации методами гидродинамического анализа приходится пользоваться упрощенными моделями грунта. К таким моделям относятся "идеальный грунт", у которого капиллярные каналы, составленные из пор, образующихся между песчинками, принимаются цилиндрическими и параллельными между собой, и "фиктивный грунт", все частички которого принимаются за шары одинакового диаметра.
Отношение суммы объёмов пор по всему объёму данного грунта называется пористостью:
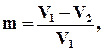 .
.
где V1 - объём грунта, V2 - суммарный объём частиц, составляющих грунт.
Пористость фиктивного грунта не зависит от диаметра взятых шаров, а зависит только от их расположения в рассматриваемом объёме и определяется по формуле:
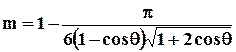 , (9.1.1)
, (9.1.1)
где q - угол, зависящий от взаимного расположения шаров.
Отношение 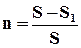 , где S - площадь всего рассматриваемого сечения грунта, S1 - площадь, занимаемая в этом сечении шарами, называется просветом и физически характеризует собой площадь, через которую фильтруется жидкость. Для фиктивного грунта
, где S - площадь всего рассматриваемого сечения грунта, S1 - площадь, занимаемая в этом сечении шарами, называется просветом и физически характеризует собой площадь, через которую фильтруется жидкость. Для фиктивного грунта
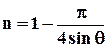 (9.1.2)
(9.1.2)
и зависит только от взаимного расположения шаров.
Для идеального грунта при ламинарном движении скорость жидкости в поровой трубке определяется по формуле:
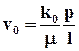 , (9.1.3)
, (9.1.3)
где 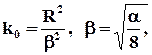 R - гидравлический радиус поперечного сечения поровой трубки, P - падение гидродинамического давления на длине l поровой трубки, m - динамический коэффициент вязкости, a - число, входящее в степенную формулу, определяющую коэффициент сопротивления
R - гидравлический радиус поперечного сечения поровой трубки, P - падение гидродинамического давления на длине l поровой трубки, m - динамический коэффициент вязкости, a - число, входящее в степенную формулу, определяющую коэффициент сопротивления
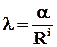 (9.1.4)
(9.1.4)
и зависящее от режима течения жидкости и показателя i.
Скорость ламинарной фильтрации в идеальном грунте, выраженная через действительную скорость течения жидкости по поровому каналу, равна
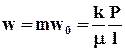 , (9.1.5)
, (9.1.5)
где 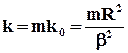 имеет размерность площади и называется проницаемостью.
имеет размерность площади и называется проницаемостью.
Под проницаемостью пористой среды понимается свойство пропускать через себя жидкость или газ под действием приложенного градиента давления, то есть это проводимость пористой среды по отношению к жидкости или газу.
При чисто квадратичной фильтрации (турбулентный режим) действительная скорость течения в поровой трубке не зависит от вязкости жидкости.
Скорость фильтрации в этом случае определяется по формуле:
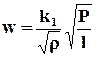 , (9.1.6)
, (9.1.6)
где 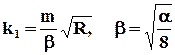 . Число a имеет в этом случае иное значение, чем при ламинарной фильтрации.
. Число a имеет в этом случае иное значение, чем при ламинарной фильтрации.
Для определения средней скорости течения жидкости через поровую трубку фиктивного грунта пользуются формулой Слихтера:
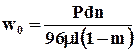 . (9.1.7)
. (9.1.7)
Здесь d - диаметр шара фиктивного грунта.
Скорость фильтрации в фиктивном грунте равна
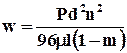 (9.1.8)
(9.1.8)
или
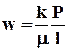 , (9.1.9)
, (9.1.9)
где величина 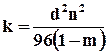 называется теоретической проницаемостью Слихтера.
называется теоретической проницаемостью Слихтера.
Для фиктивного грунта, пористость которого изменяется в интервале 0.26 < m <0.48, приближённое значение теоретической проницаемости определяется по формуле:
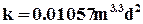 . (9.1.10)
. (9.1.10)
При определении средней скорости движения по поровому каналу, в связи с его криволинейностью, необходимо вместо действительной толщины пласта (грунта) h вводить фиктивную толщину:
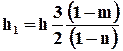 .
.
Расход жидкости через фиктивный грунт
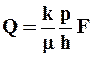 или
или 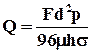 , (9.1.11)
, (9.1.11)
где F - площадь сечения грунта, 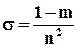 . При измерении [d] и [h] в сантиметрах [F] - в квадратных сантиметрах, [m] - [дина×с/см2], [р]- см. вод. ст. при 4°С и [Q] -[см3/с] , формула расхода принимает вид
. При измерении [d] и [h] в сантиметрах [F] - в квадратных сантиметрах, [m] - [дина×с/см2], [р]- см. вод. ст. при 4°С и [Q] -[см3/с] , формула расхода принимает вид
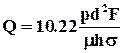 .
.
Приведённые формулы скорости и расхода применимы для частиц, средний диаметр которых изменяется в пределах 0,01мм - 5 мм.
Формула (2.26) является основной формулой для определения скорости фильтрации в фиктивном грунте.
Для определения коэффициента проницаемости этой формулы существует ряд зависимостей, из которых наиболее распространёнными являются:
· формула Козени, уточнённая Л.С.Лейбензоном:
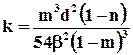 , (9.1.12)
, (9.1.12)
где b2 = 5/3, исходя из предположения, что поперечное сечение порового канала есть равносторонний треугольник; для случая квадратного сечения b2 = 16/9.
· формула Терцаги I:
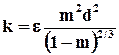 , (9.1.13)
, (9.1.13)
где коэффициент e зависит от структуры грунта; для песка с гладкой поверхностью e = 10.5; с угловатой - 6.0.
· формула Терцаги II:
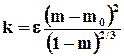 , (9.1.14)
, (9.1.14)
где m0 = 0.13; при m = m0, т.е. когда пористость грунта очень мала, фильтрация, согласно этой формуле, прекращается.
· Формула Лейбензона, выведенная из приложения теории обтекания к фильтрации в фиктивном грунте:
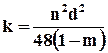 (9.1.15)
(9.1.15)
Пользуясь методом размерности, Лейбензон получил следующую общую формулу теории фильтрации:
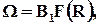
где В1 - некоторая постоянная, а W и R - безразмерные величины, определяемые равенствами:
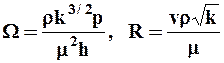 .
.
Указанные формулы могут быть использованы при исследовании фильтрации жидкости через естественный грунт с последующей заменой диаметра d шара фиктивного грунта через так называемый эффективный или действующий диаметр частиц естественного грунта.
Дата добавления: 2016-01-09; просмотров: 2742;
