Построение индуктивностей на отрезках полосковых линий
Вследствие малых номиналов в УВЧ диапазоне индуктивности колебательных систем и блокировочные индуктивности (дроссели) невозможно выполнить в виде сосредоточенных элементов (катушек и спиралей).
Вместо них используют отрезки полосковых и микрополосковых линий [5]. Напомним, что для однородной линии, замкнутой на корпус на одном конце (рис. 1.23), входное сопротивление
|
|
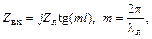 (1.67)
(1.67)
где Zл – волновое сопротивление линии,
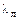 – длина волны в линии, l – длина отрезка линии.
– длина волны в линии, l – длина отрезка линии.

Рис. 1.23. Отрезок микрополосковой линии
Для такой же линии, разомкнутой на конце,
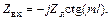 (1.68)
(1.68)
При реализации блокировочных элементов в схемах (рис. 1.1), когда индуктивности Г-образных фильтров должны быть большими, обычно используют замкнутые на корпус отрезки линий длиной 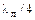 . Входное сопротивление линии в точке подключения по первой гармонике (и всем нечетным гармоникам) стремится к бесконечности и близко к нулевому для второй гармоники и всех четных, что на практике улучшает их фильтрацию.
. Входное сопротивление линии в точке подключения по первой гармонике (и всем нечетным гармоникам) стремится к бесконечности и близко к нулевому для второй гармоники и всех четных, что на практике улучшает их фильтрацию.
Несколько сложнее выглядит ситуация, когда нужно реализовать контурную индуктивность в П-образном контуре (рис. 1.24, аналогичный рис. 1.3).
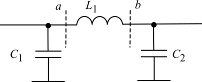
Рис. 1.24. Схема П-образного контура
Сопротивления 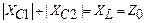 известны из расчета колебательной системы, а емкости
известны из расчета колебательной системы, а емкости 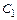 и
и 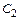 представляют собой конденсаторы.
представляют собой конденсаторы.
Для определения отрезка микроволновой линии, заменяющей 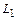 , можно использовать общую формулу расчета входного сопротивления отрезка однородной линии, нагруженной на сопротивление
, можно использовать общую формулу расчета входного сопротивления отрезка однородной линии, нагруженной на сопротивление 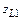 (в данном случае
(в данном случае 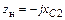 ). Однако более наглядным представляется следующий подход. Заменим емкость сопротивлением отрезка линии, разомкнутой на конце.
). Однако более наглядным представляется следующий подход. Заменим емкость сопротивлением отрезка линии, разомкнутой на конце.
Согласно (1.68)
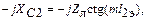
 (1.69)
(1.69)
где 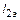 – длина отрезка линии, имитирующей емкость С2.
– длина отрезка линии, имитирующей емкость С2.
Из (1.69) находим 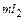 . Эта величина меньше
. Эта величина меньше 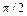 , что обеспечивает отрицательное реактивное входное сопротивление от точки b справа. Теперь П-образный контур можно представить в виде рис. 1.25.
, что обеспечивает отрицательное реактивное входное сопротивление от точки b справа. Теперь П-образный контур можно представить в виде рис. 1.25.

Рис. 1.25. Эквивалентная схема П-образного контура
на отрезках микрополосковых линий
Сопротивление в точке a слева равно 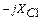 , а справа
, а справа 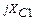 из условия резонанса в контуре, следовательно,
из условия резонанса в контуре, следовательно,
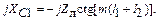 (1.70)
(1.70)
Из (1.70) вычисляют 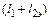 . Обратим внимание на то, что
. Обратим внимание на то, что 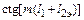 должен быть отрицательным, т.е.
должен быть отрицательным, т.е. 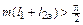 . В результате рассчитываем требуемую длину отрезка микрополосковой линии
. В результате рассчитываем требуемую длину отрезка микрополосковой линии 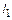 .
.
Определим конструкцию индуктивности в примере контура, рассчитанного в п. 1.1. Напомним, что 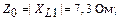
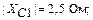
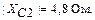 Выберем микрополосковую линию с
Выберем микрополосковую линию с 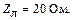
Определим 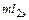 из (1.69):
из (1.69):
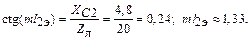
|
Далее из (1.70) находим 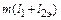 :
:
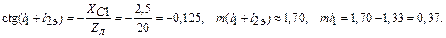
|
|
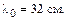 В микрополосковой линии она зависит от диэлектрической проницаемости
В микрополосковой линии она зависит от диэлектрической проницаемости 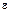 используемого изолятора
используемого изолятора 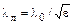 .
.
Для сапфира 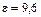 и
и 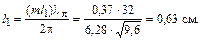
На отрезках полосковых линий можно целиком выполнить П-контур (рис. 1.26) [5].
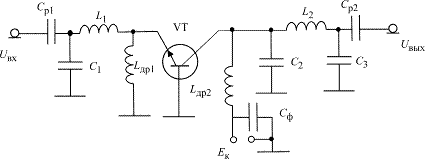
Рис. 1.26. Схема УМ на биполярном транзисторе с ОБ
Вариант возможной конструктивной реализации УМ (рис. 1.27) предусматривает выполнение входной и выходной согласующих цепей на отрезках полосковых линий W1 и W2 с разомкнутыми шлейфами Wш1 и Wш2. Параметры линий и шлейфов различны.
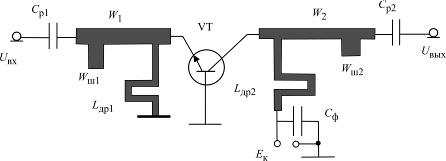
Рис. 1.27. Пример конструктивной реализации УМ
на биполярном транзисторе с ОБ
Блокировочные дроссели Lдр1 и Lдр2 чаще всего выполняют в виде печатных индуктивностей и в этом исполнении полосковыми линиями они не являются.
Дата добавления: 2016-01-07; просмотров: 3005;
