Напряженность режима работы УМ
Электронный режим АП является динамическим, т.е. напряжения на электродах АП являются переменными, а рабочая точка перемещается по вольтамперной характеристике (ВАХ) АП.
Динамические режимы (рис. 1.12−1.13) классифицируют по степени напряженности в зависимости от соотношения мгновенных значений напряжений на входе и выходе АП как недонапряженный (НР), граничный (ГР) и перенапряженный (ПР) [3]. Для недонапряженного режима характерно соотношение 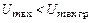 , где
, где  − амплитуда сигнала возбуждения;
− амплитуда сигнала возбуждения; 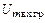 – амплитуда сигнала возбуждения, соответствующая граничному режиму; для перенапряженного
– амплитуда сигнала возбуждения, соответствующая граничному режиму; для перенапряженного 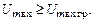
|
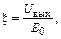 (1.25)
(1.25)
где 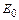 – напряжение питания,
– напряжение питания, 
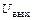 – амплитуда РЧ напряжения на выходе АП.
– амплитуда РЧ напряжения на выходе АП.
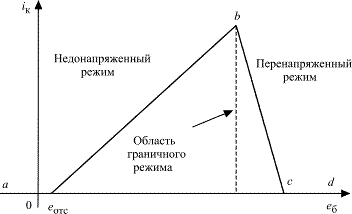
Рис. 1.12
В плоскости выходных ВАХ (рис. 1.13) геометрическое место точек граничного режима находится на линии граничного режима (ЛГР), справа от нее располагается область недонапряженных режимов, а слева – перенапряженных.
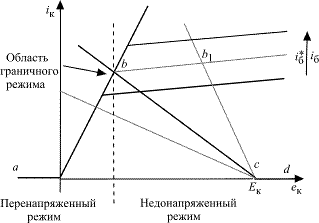
Рис. 1.13
Рассмотрим рис. 1.14. Очевидно, что остаточное напряжение на коллекторе, например, БП транзистора в граничном режиме 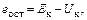 а также
а также 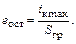
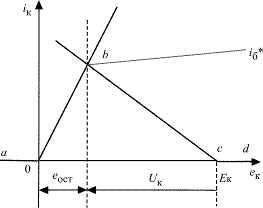
Рис. 1.14
Тогда 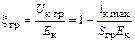 и, следовательно, всегда
и, следовательно, всегда 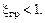
Поскольку 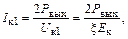
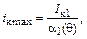 из предыдущего выражения получаем
из предыдущего выражения получаем
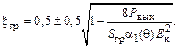 (1.26)
(1.26)
Для УМ характерны режимы работы, которым соответствует знак «плюс» в полученной формуле для расчета 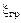 по заданной выходной мощности.
по заданной выходной мощности.
Максимум выходной мощности и КПД УМ достигают в слабоперенапряженных режимах, близких к граничному [3, 4].
1.4. Усилители мощности
на полевых транзисторах ОВЧ-УВЧ диапазонов
В усилителях мощности (УМ) используют полевые транзисторы с изолированным затвором. Это значит, что затвор не пропускает постоянный ток, а входное сопротивление транзистора носит емкостной характер. Казалось бы, что при этом потери во входной цепи должны быть минимальными, а коэффициент усиления мощности 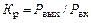 весьма большим (теоретически бесконечным).
весьма большим (теоретически бесконечным).
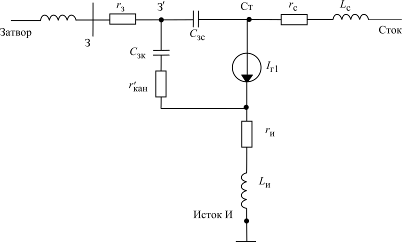
Рис. 1.15. Эквивалентная схема мощного ОВЧ-УВЧ полевого транзистора
На практике все обстоит гораздо сложнее, особенно в диапазонах ОВЧ и УВЧ, где на величину 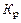 оказывают сильное влияние паразитные элементы транзистора: индуктивности выводов, межэлектродные емкости и потери в транзисторе (рис. 1.15). По своим номиналам эти элементы могут быть весьма малыми, но тем не менее их влияние на величину
оказывают сильное влияние паразитные элементы транзистора: индуктивности выводов, межэлектродные емкости и потери в транзисторе (рис. 1.15). По своим номиналам эти элементы могут быть весьма малыми, но тем не менее их влияние на величину 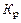 становится определяющим.
становится определяющим.
Для последующего анализа схему (рис. 1.15) упростим еще больше. Индуктивности выводов затвора 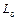 и
и 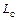 можно отнести к внешним цепям. Они влияют на настройку соответствующих колебательных систем, но напрямую не сказываются на усилительных свойствах транзистора. Сопротивления потерь
можно отнести к внешним цепям. Они влияют на настройку соответствующих колебательных систем, но напрямую не сказываются на усилительных свойствах транзистора. Сопротивления потерь 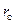 и
и 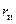 малы и их влияние на
малы и их влияние на 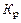 незначительно. Поэтому устраняем их из схемы. Емкость затвор-канал
незначительно. Поэтому устраняем их из схемы. Емкость затвор-канал 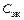 мало отличается от приводимой в справочниках эквивалентной входной емкости затвор-исток
мало отличается от приводимой в справочниках эквивалентной входной емкости затвор-исток 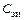 , так что будем считать
, так что будем считать 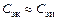 . Часть сопротивления канала, по которому проходит входной ток, на рис. 1.15 обозначена как
. Часть сопротивления канала, по которому проходит входной ток, на рис. 1.15 обозначена как 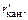 Оставляем элементы обратных связей в схеме: индуктивность общего вывода
Оставляем элементы обратных связей в схеме: индуктивность общего вывода 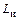 и проходную емкость
и проходную емкость 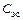 . В результате получаем схему рис. 1.16.
. В результате получаем схему рис. 1.16.
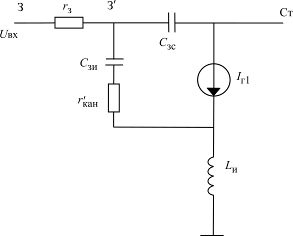
Рис. 1.16. Упрощенная эквивалентная схема
мощного ОВЧ-УВЧ полевого транзистора
Из-за наличия во входной цепи частотно-зависимого делителя 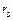 , Сзи и
, Сзи и 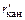 управляющее напряжение полевого транзистора
управляющее напряжение полевого транзистора 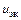 с комплексной амплитудой
с комплексной амплитудой 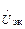 отличается от входного
отличается от входного 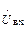 :
: 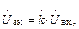 причем коэффициент передачи входного напряжения на емкость Сзи
причем коэффициент передачи входного напряжения на емкость Сзи
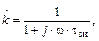 (1.27)
(1.27)
|
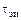 − постоянная времени входной цепи собственно транзистора
− постоянная времени входной цепи собственно транзистора
Следовательно, с ростом частоты модуль и фазовый угол управляющего напряжения полевого транзистора изменяются.
Соответственно амплитуда тока стока
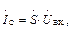 (1.28)
(1.28)
где 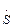 − комплексная крутизна
− комплексная крутизна 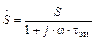 . (1.30)
. (1.30)
Постоянная времени τзи определяет граничную частоту полевого транзистора по крутизне
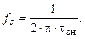 (1.31)
(1.31)
Ток затвора (в режиме короткого замыкания на выходе)
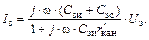 (1.32)
(1.32)
|
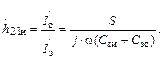 (1.33)
(1.33)
Отсюда видно, что граничная частота 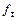 , на которой модуль
, на которой модуль 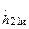 уменьшается до единицы:
уменьшается до единицы:
|
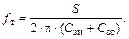 (1.34)
(1.34)
Сравнив 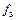 и
и 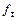 , находим
, находим 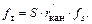
В полевых транзисторах слабо проявляются процессы накапливания и рассасывания заряда, свойственные биполярным приборам, поэтому уменьшение усиления полевых транзисторов с ростом частоты при неизменной амплитуде входного напряжения определяется главным образом увеличением вещественной составляющей входной проводимости gвх. Примем для простоты величину проходной емкости Сзс малой.
При Сзс = 0 входная проводимость усилителя на полевом транзисторе
|
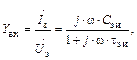
откуда
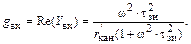 (1.35)
(1.35)
Видно, что на частотах 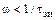 проводимость gвх быстро увеличивается с ростом частоты (примерно пропорционально квадрату частоты). Соответственно увеличивается
проводимость gвх быстро увеличивается с ростом частоты (примерно пропорционально квадрату частоты). Соответственно увеличивается 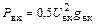 (при неизменной амплитуде входного сигнала Uвх) и уменьшается коэффициент усиления мощности Кр. На частотах f << fs проводимость gвх мала (gвх → 0 при f → 0) и полевым транзистором от источника возбуждения потребляется незначительная мощность, поэтому на низких частотах коэффициент усиления мощности получается высоким. Однако уже на частотах f = (0,3…0,5)fs он часто снижается до нескольких десятков единиц и более.
(при неизменной амплитуде входного сигнала Uвх) и уменьшается коэффициент усиления мощности Кр. На частотах f << fs проводимость gвх мала (gвх → 0 при f → 0) и полевым транзистором от источника возбуждения потребляется незначительная мощность, поэтому на низких частотах коэффициент усиления мощности получается высоким. Однако уже на частотах f = (0,3…0,5)fs он часто снижается до нескольких десятков единиц и более.
Дальнейшее изложение проведем на примере расчета коэффициента усиления мощности УМ на полевом транзисторе.
Исходные данные УМ:
выходная мощность Рвых = 40 Вт,
напряжение питания стока Ес = 36 В,
относительное напряжение на стоке 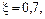
рабочая частота f = 420 МГц ( 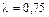 м),
м),
угол отсечки выходного тока 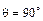 .
.
Параметры транзистора:
крутизна S = 2 А/В,
емкости Cзи = 450 пФ; Сзс = 60 пФ,
сопротивления 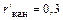 Ом; rз = 0,1 Ом,
Ом; rз = 0,1 Ом,
индуктивность вывода истока 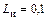 нГн.
нГн.
Этап 1. Определение основных электрических характеристик УМ.
Амплитуда первой гармоники напряжения на стоке
|
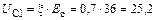 В.
В.
Первая гармоника тока стока
|
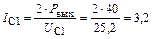 А.
А.
Эквивалентное сопротивление нагрузки
|
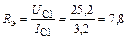 Ом.
Ом.
В дальнейших расчетах будем считать, что 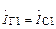 , так как проходная емкость Сзс является частью выходной колебательной системы (она входит в общую емкость С1 рис. 1.2).
, так как проходная емкость Сзс является частью выходной колебательной системы (она входит в общую емкость С1 рис. 1.2).
Этап 2. Расчет потерь во входной цепи без учета элементов обратной связи. Положим вначале, что проходная емкость Сзс и индуктивность  равны нулю. По-прежнему считаем, что
равны нулю. По-прежнему считаем, что  .
.
Напряжение на емкости затвор-канал Сзк
|
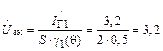 В.
В.
Первая гармоника тока затвора
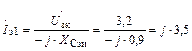
|
причем
|
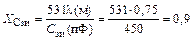 Ом.
Ом.
Обратим внимание на то, что ток затвора 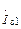 на
на 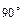 опережает по фазе ток
опережает по фазе ток 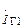 . Это очень важное обстоятельство, влияющее на процессы в цепях обратной связи.
. Это очень важное обстоятельство, влияющее на процессы в цепях обратной связи.
Потери в канале от входного тока 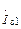
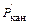
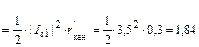 Вт.
Вт.
Если бы все потери во входной цепи ограничивались только потерями в канале 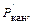 то Kр был бы порядка 10. На самом деле он будет существенно ниже.
то Kр был бы порядка 10. На самом деле он будет существенно ниже.
Этап 3. Расчет потерь на входе, определяемых индуктивностью вывода истока Lи. Через индуктивность Lи протекают два тока: 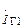 и
и 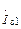 , что обусловливает наличие обратной связи между входной и выходной цепями.
, что обусловливает наличие обратной связи между входной и выходной цепями.
Эквивалентное сопротивление, вносимое индуктивностью Lи во входную цепь, определим в соответствии с законами Кирхгофа:
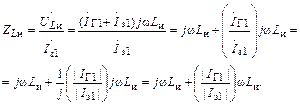 (1.36)
(1.36)
Из выражения (1.36) следует, что Lи вносит во входную цепь не только индуктивное сопротивление jωLи, но и активные потери
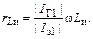
Эквивалентное сопротивление 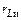 появляется из-за того, что токи
появляется из-за того, что токи  и
и 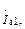 протекающие через Lи, сдвинуты по фазе на 90º. В данном случае возникает отрицательная обратная связь. В то же время часть мощности возбуждения через индуктивность Lи идет непосредственно в выходную цепь без усиления в транзисторе.
протекающие через Lи, сдвинуты по фазе на 90º. В данном случае возникает отрицательная обратная связь. В то же время часть мощности возбуждения через индуктивность Lи идет непосредственно в выходную цепь без усиления в транзисторе.
На Lи возникает дополнительная ЭДС, включенная последовательно с транзистором. Хорошо ли это? Отрицательная обратная связь повышает устойчивость усилителя, но заметно снижает коэффициент усиления мощности.
Найдем дополнительные потери мощности:
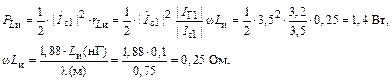
|
Величина 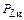 сопоставима с
сопоставима с 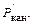 Где выделяется эта мощность? В нагрузке усилителя, в выходной цепи за счет прямой передачи мощности из входной цепи.
Где выделяется эта мощность? В нагрузке усилителя, в выходной цепи за счет прямой передачи мощности из входной цепи.
Этап 4. Расчет потерь на входе, определяемых проходной емкостью 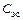 . Емкость
. Емкость 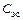 непосредственно соединяет выход (сток) транзистора со входом (затвором). Это тоже элемент обратной связи. Оценим его вклад в энергетические характеристики усилителя.
непосредственно соединяет выход (сток) транзистора со входом (затвором). Это тоже элемент обратной связи. Оценим его вклад в энергетические характеристики усилителя.
Мощность, поступающая через 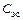 , рассчитывают по формуле
, рассчитывают по формуле
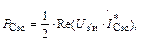
|
где 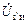 – напряжение между точкой з′ (рис. 1.16) и корпусом;
– напряжение между точкой з′ (рис. 1.16) и корпусом;
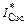 – комплексно-сопряженная величина тока через емкость
– комплексно-сопряженная величина тока через емкость 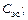 Re означает реальную часть результата;
Re означает реальную часть результата;
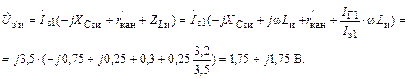 (1.39)
(1.39)
Ток через емкость 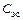
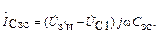 (1.40)
(1.40)
|
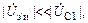 так что
так что
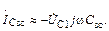 (1.41)
(1.41)
При расчете тока 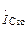 обязательно надо учесть, что выходное напряжение
обязательно надо учесть, что выходное напряжение 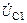 противофазно току
противофазно току 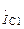 , фаза которого была принята за нуль, следовательно,
, фаза которого была принята за нуль, следовательно,
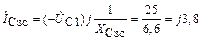 А,
А,
поскольку
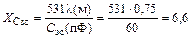 Ом.
Ом.
Как следует из (1.38), (1.40) и (1.41):
|
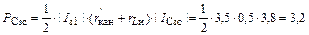 Вт. (1.42)
Вт. (1.42)
Суммарный входной ток
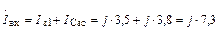
|
Дополнительные потери на 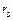 :
:
|
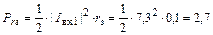 Вт.
Вт.
|
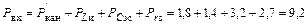 Вт,
Вт,
а коэффициент усиления мощности
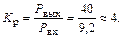
Как видно, величина 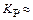 6 дБ, что характерно для УМ УВЧ диапазона.
6 дБ, что характерно для УМ УВЧ диапазона.
Для более точных расчетов следует учесть взаимное влияние элементов обратной связи Lи и Сзс, а также то, что собственно транзистор должен генерировать меньшую мощность: 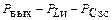 [4].
[4].
1.5. Усилители мощности на биполярных транзисторах
ОВЧ-УВЧ диапазонов. Схема с общим эмиттером.
Расчет в режиме без отсечки тока (режим А)
Как и при анализе УМ на полевом транзисторе, индуктивности выводов базы 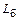 и коллектора
и коллектора 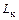 следует отнести ко внешним цепям (рис. 1.17). Переход эмиттер-база представлен соединением зарядной емкости
следует отнести ко внешним цепям (рис. 1.17). Переход эмиттер-база представлен соединением зарядной емкости 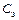 и диодом. В режиме А диод постоянно открыт и его можно заменить соединением диффузионной емкости
и диодом. В режиме А диод постоянно открыт и его можно заменить соединением диффузионной емкости 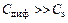 и сопротивлением потерь диода
и сопротивлением потерь диода 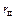 .
.
В результате эквивалентная схема транзистора для дальнейшей работы сведена к схеме рис. 1.18.
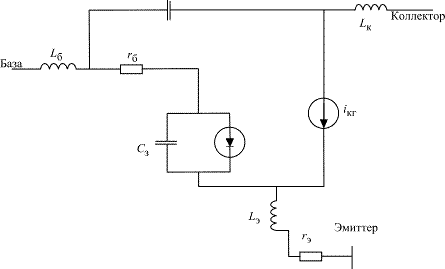
Рис. 1.17. Эквивалентная схема биполярного транзистора
Одним из важнейших параметров биполярного транзистора является коэффициент передачи тока в схеме с ОЭ
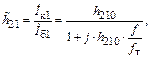 (1.43)
(1.43)
где 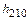 – коэффициент передачи тока на нулевой частоте; обычно
– коэффициент передачи тока на нулевой частоте; обычно 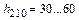 ; ток генератора
; ток генератора 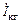 связан с напряжением на переходе
связан с напряжением на переходе 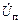 соотношением
соотношением
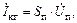
|
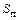 – крутизна по переходу, составляющая несколько десятков А/В.
– крутизна по переходу, составляющая несколько десятков А/В.
На нулевой частоте 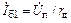 , так что
, так что 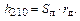
С повышением рабочей частоты коэффициент передачи тока 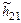 начинает уменьшаться (рис. 1.18). Чтобы получить требуемый ток
начинает уменьшаться (рис. 1.18). Чтобы получить требуемый ток 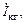 необходимо поддерживать постоянную амплитуду
необходимо поддерживать постоянную амплитуду 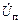 . Поскольку емкости Сэ и Сдиф шунтируют переход, ток, проходящий через них, растет прямо пропорционально рабочей частоте. На частоте
. Поскольку емкости Сэ и Сдиф шунтируют переход, ток, проходящий через них, растет прямо пропорционально рабочей частоте. На частоте 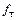 модуль коэффициента передачи тока
модуль коэффициента передачи тока 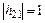 (
( 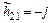 ).
).
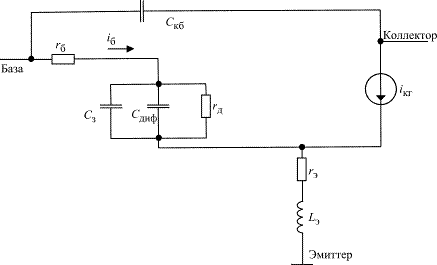
Рис. 1.18. Эквивалентная схема биполярного транзистора в режиме А
Из сопоставления параметров перехода эмиттер-база, выражений (1.43) и (1.44), получаем
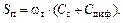 (1.45)
(1.45)
На частотах 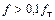 произведение
произведение 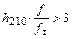 , так что (1.43) можно преобразовать к виду
, так что (1.43) можно преобразовать к виду
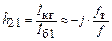 . (1.46)
. (1.46)
Для большинства УМ передатчиков станций подвижной связи выражение (1.46) вполне приемлемо и его будем использовать в расчетах. Далее поступим так же, как делали при анализе УМ на полевом транзисторе.
Выполним пример расчета коэффициента усиления мощности УМ на биполярном транзисторе.
Исходные данные УМ:
выходная мощность 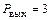 Вт,
Вт,
напряжение питания коллектора 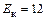 В,
В,
относительное напряжение на коллекторе 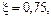
рабочая частота 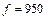 МГц,
МГц,
режим работы транзистора − класс А.
Параметры транзистора:
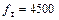 МГц,
МГц, 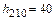 ,
, 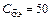 пФ,
пФ, 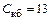 пФ,
пФ, 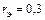 Ом,
Ом, 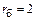 Ом, Lэ = 0,3 нГн.
Ом, Lэ = 0,3 нГн.
|
Амплитуда первой гармоники напряжения на коллекторе
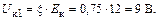
Первая гармоника коллекторного тока
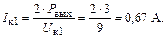
Эквивалентное сопротивление нагрузки
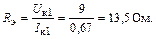
Далее будем считать, что 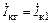 , так как емкость
, так как емкость 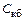 входит в состав колебательной системы.
входит в состав колебательной системы.
 Этап 2. Расчет потерь на входе без учета элементов обратной связи.
Этап 2. Расчет потерь на входе без учета элементов обратной связи.
Определим первую гармонику тока базы (1.46):
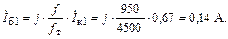
Найдем потери в теле базы:
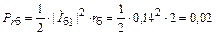 Вт
Вт
Как видим, эти потери весьма малы.
Этап 3. Расчет потерь на входе, определяемых элементами вывода эмиттера.  Через индуктивность Lэ и сопротивление
Через индуктивность Lэ и сопротивление 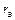 протекают два тока:
протекают два тока: 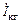 и
и 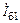 . Между собой они сдвинуты по фазе на
. Между собой они сдвинуты по фазе на 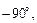 следовательно, как и в УМ на полевом транзисторе, возникает отрицательная обратная связь.
следовательно, как и в УМ на полевом транзисторе, возникает отрицательная обратная связь.
Эквивалентное сопротивление эмиттерной цепи для тока 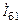 :
:
|
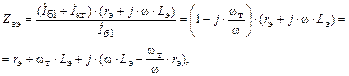 (1.47)
(1.47)
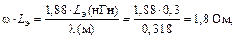
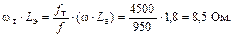
Мощность, передаваемая через 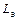 со входа на выход
со входа на выход
|
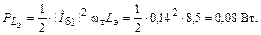
Мощность, рассеиваемая на 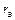 проходящим током
проходящим током 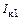
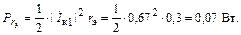
|
Этап 4. Расчет потерь на входе, определяемых отрицательной обратной связью через проходную емкость 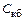 .
.
Логика рассуждений тут та же, что и при анализе УМ на полевом транзисторе. Аналогично (1.38) мощность, передаваемая через 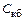
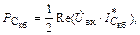 (1.48)
(1.48)
где 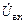 − амплитуда напряжения на входе транзистора,
− амплитуда напряжения на входе транзистора, 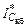 − комплексно-сопряженная величина тока через емкость
− комплексно-сопряженная величина тока через емкость 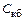 .
.
Входное напряжение
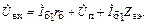
|
В (1.40) 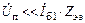 (в расчетах можно считать, что напряжение на эмиттерном переходе равно нулю), тогда
(в расчетах можно считать, что напряжение на эмиттерном переходе равно нулю), тогда
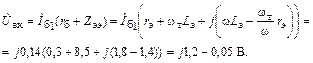
Поскольку 
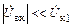 ,
,
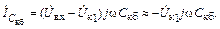
|
|
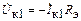 (выходные напряжение и ток противофазны), так что
(выходные напряжение и ток противофазны), так что
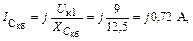
|
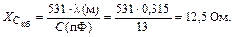
Рассчитаем мощность 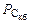 :
:
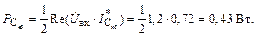
|
Полная входная мощность
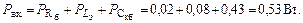
При этом суммарная мощность 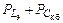 через элементы обратной связи поступает непосредственно в нагрузку усилителя.
через элементы обратной связи поступает непосредственно в нагрузку усилителя.
Коэффициент усиления мощности
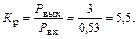
Для более точного расчета, учитывающего взаимное влияние Lэ и 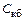 , а также уменьшение тока
, а также уменьшение тока 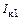 из-за прямого прохождения мощности
из-за прямого прохождения мощности 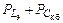 в нагрузку, следует обратиться к методике [4].
в нагрузку, следует обратиться к методике [4].
Вопрос. Как вы думаете, можно ли этот транзистор использовать в УМ на частоте 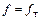 ?
?
1.6. Усилители мощности на биполярных транзисторах
ОВЧ-УВЧ диапазонов. Схема с общим эмиттером.
Расчет режима с отсечкой тока
Из-за низкого КПД режим А транзистора в УМ используют редко. При работе биполярных транзисторов с отсечкой коллекторного тока в схеме происходят переключения состояния перехода эмиттер-база (рис. 1.17). В те моменты времени, когда транзистор отперт, диод открыт и эмиттерный переход представляют эквивалентной схемой рис. 1.19, а. Во время отсечки выходного тока эмиттерный переход эквивалентен зарядной емкости Cэ (рис. 1.19, б).
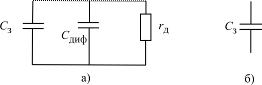
Рис. 1.19. Эквивалентная схема перехода эмиттер-база:
а − открытый, б − запертый
В связи с нелинейным характером поведения эмиттерного перехода строгий анализ работы УМ требует довольно объемного изучения. Однако выполненные к настоящему времени многочисленные теоретические, а самое главное, экспериментальные исследования, позволяют предложить достаточно простой алгоритм расчета энергетических характеристик УМ.
Прежде всего отметим, что предшествующий УМ каскад, как правило, представляет собой генератор тока, так что независимо от состояния эмиттерного перехода на входе транзистора действует входной гармонический ток. Ток базы также можно считать гармоническим с амплитудой 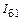 . Когда переход открыт, ввиду малости его сопротивления можно принять напряжение радиочастоты на переходе равным нулю. Это состояние длится в пределах
. Когда переход открыт, ввиду малости его сопротивления можно принять напряжение радиочастоты на переходе равным нулю. Это состояние длится в пределах 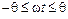 , где
, где 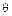 − угол отсечки коллекторного тока. Когда переход закрыт, на нем возникает обратная полуволна напряжения. Поясним приведенные рассуждения временными диаграммами рис. 1.20 для случая, когда угол отсечки коллекторного тока
− угол отсечки коллекторного тока. Когда переход закрыт, на нем возникает обратная полуволна напряжения. Поясним приведенные рассуждения временными диаграммами рис. 1.20 для случая, когда угол отсечки коллекторного тока 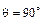 .
.
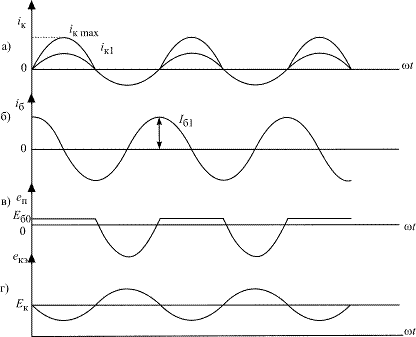
Рис. 1.20. Временные диаграммы токов и напряжений
в биполярном транзисторе в режиме с отсечкой тока
На рис. 1.20, а представлены косинусоидальные импульсы коллекторного тока и первая гармоника этого того тока 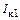 . Так как сопротивление эмиттерного перехода и в открытом, и в закрытом состояниях практически является емкостным, ток базы
. Так как сопротивление эмиттерного перехода и в открытом, и в закрытом состояниях практически является емкостным, ток базы 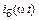 опережает первую гармонику коллекторного тока на
опережает первую гармонику коллекторного тока на 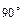 (на рис. 1.20, б ток базы приведен в увеличенном масштабе в сравнении с
(на рис. 1.20, б ток базы приведен в увеличенном масштабе в сравнении с 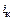 ). Чтобы обеспечить импульс коллекторного тока с максимальной величиной
). Чтобы обеспечить импульс коллекторного тока с максимальной величиной 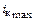 , амплитуда тока базы должна быть связана с амплитудой первой гармоники тока коллектора соотношением
, амплитуда тока базы должна быть связана с амплитудой первой гармоники тока коллектора соотношением
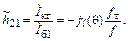 (1.50)
(1.50)
Сравнение с (1.46) показывает, что в выражении для коэффициента передачи тока появляется коэффициент разложения последовательности косинусоидальных импульсов 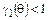 (
( 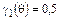 для
для 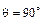 ).
).
Следовательно, для получения требуемой амплитуды первой гармоники коллекторного тока амплитуда тока базы в режиме с отсечкой должна быть больше, чем в режиме А:
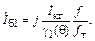
|
Зависимость напряжения на эмиттерном переходе 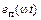 приведена на рис. 1.20, в. Когда транзистор открыт, амплитуда напряжения на входе настолько мала, что на графике это прямая линяя (обратите внимание, что мгновенное напряжение будет
приведена на рис. 1.20, в. Когда транзистор открыт, амплитуда напряжения на входе настолько мала, что на графике это прямая линяя (обратите внимание, что мгновенное напряжение будет 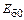 , так как транзистор открыт!). Когда транзистор закрыт, на эмиттерном переходе появляется отрицательный косинусоидальный импульс напряжения длительностью
, так как транзистор открыт!). Когда транзистор закрыт, на эмиттерном переходе появляется отрицательный косинусоидальный импульс напряжения длительностью 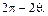
Что касается напряжения на коллекторе, то оно по-прежнему является суммой напряжений 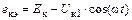 , поскольку колебательная система на выходе транзистора фильтрует все гармоники радиочастоты, кроме первой (рис. 1.20, г).
, поскольку колебательная система на выходе транзистора фильтрует все гармоники радиочастоты, кроме первой (рис. 1.20, г).
Для расчета коэффициента усиления УМ можно использовать методику и формулы, приведенные в предыдущем параграфе для УМ, где биполярный транзистор работает в режиме А. Только в них надо будет внести 3 поправки. Первая касается расчета тока базы: вместо (1.46) надо использовать (1.51). Эта замена ведет ко второй поправке в формуле (1.47):
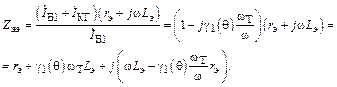 (1.52)
(1.52)
|
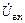 (1.49) первая гармоника напряжения на переходе
(1.49) первая гармоника напряжения на переходе
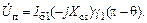 (1.53)
(1.53)
Заметим, что изменение 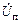 мало влияет на коэффициент усиления мощности, поскольку эта составляющая входного напряжения сдвинута по фазе на
мало влияет на коэффициент усиления мощности, поскольку эта составляющая входного напряжения сдвинута по фазе на 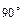 относительно тока, протекающего через проходную емкость
относительно тока, протекающего через проходную емкость 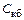 .
.
Вопрос. Как изменится коэффициент усиления мощности в примере, рассмотренном в параграфе 1.5, если транзистор стал работать в режиме В? Как изменится КПД УМ?
Чтобы убедиться в правильности ответа, произведите расчет УМ, когда транзистор работает в режиме В, и сравните результаты.
 1.7. Особенности работы усилителей по схеме с общей базой
1.7. Особенности работы усилителей по схеме с общей базой
Из параграфов 1.5 и 1.6 следует, что при приближении рабочей частоты к fт коэффициент усиления мощности в схеме с ОЭ резко падает. В таких случаях более эффективно использовать схему с общей базой (ОБ), где за счет индуктивности общего вывода (индуктивности базы) создается положительная обратная связь (рис. 1.21).
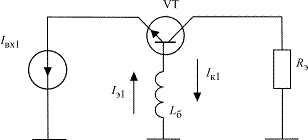
Рис. 1.21. Эквивалентная схема усилителя на транзисторе с общей базой
Через индуктивность базового вывода Lб протекают 2 тока: входной (эмиттера Iэ1) и коллектора Iк1. Сопротивление, которое вносит индуктивность Lб во входную цепь
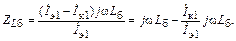
|
Для простоты исследования рассмотрим режим А:
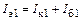 и
и 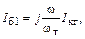
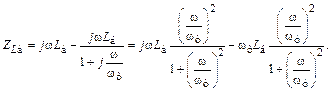 (1.55)
(1.55)
Второе слагаемое в (1.55) – отрицательное активное сопротивление, снижающее эквивалентные потери во входной цепи, что увеличивает коэффициент усиления мощности.
Расчет усилителей с ОБ следует вести по методике, приведенной в [4]. При этом надо обеспечить устойчивость усилителя, которая может быть нарушена из-за положительной обратной связи.
Обычно транзисторы, включаемые с ОЭ, имеют вывод эмиттера, соединенный с корпусом. У транзисторов с ОБ с корпусом соединен вывод базы.
1.8. Согласующе-фильтрующие системы
и коэффициент фильтрации гармоник
Колебательная система на выходе УМ выполняет две функции: согласует (трансформирует) сопротивление нагрузки (входное сопротивление антенны или фидера в оконечном каскаде) в эквивалентное сопротивление нагрузки транзистора Rэ для обеспечения необходимого режима его работы (недонапряженного, перенапряженного, граничного) и фильтрует высшие гармоники, обусловленные нелинейным режимом работы транзистора из-за отсечки выходного тока.
Существуют нормы, в частности, для ОК УМ, регламентирующие допустимую мощность каждой высшей гармоники, излучаемой антенной. Для базовых станций УВЧ диапазона эта норма близка к 1 мВт.
Классической схемой, фильтрующей гармоники, является П-контур (рис. 1.22).
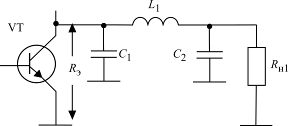
Рис. 1.22. Усилитель мощности с П-контуром
|
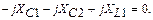
Как было показано в параграфе 1.1, согласующие свойства контура определены коэффициентами включения конденсаторов С1 и С2.
Обратимся к фильтрации высших гармоник. Мощность первой гармоники 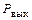
|
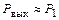 .
.
Ток первой гармоники на выходе транзистора
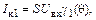
|
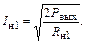
Коэффициент передачи тока по первой гармонике
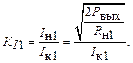 (1.56)
(1.56)
Для каждой из высших гармоник коллекторный ток 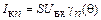 .
.
Ток в нагрузке
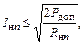
где 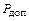 – допустимая мощность n-й гармоники,
– допустимая мощность n-й гармоники, 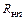 – активная часть сопротивления антенны (фидера) на n-й гармонике.
– активная часть сопротивления антенны (фидера) на n-й гармонике.
Аналогично
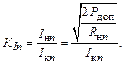 (1.57)
(1.57)
Определим требуемый коэффициент фильтрации n-й гармоники
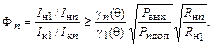 (1.58)
(1.58)
|
В соответствии с законом Кирхгофа найдем амплитуду первой гармоники ЭДС 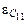 на конденсаторе С1:
на конденсаторе С1:
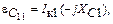 (1.59)
(1.59)
которая определяет ток в контуре
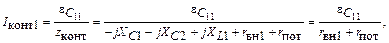 (1.60)
(1.60)
где rвн1 – эквивалентное сопротивление, вносимое в контур из нагрузки;
rпот – собственные потери в контуре; 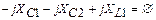 .
.
ЭДС на емкости C2
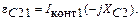 (1.61)
(1.61)
|
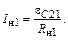 (1.62)
(1.62)
Используя выражения (1.59)−(1.62), находим
|
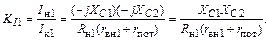 (1.63)
(1.63)
Проделав те же операции для n-й гармоники, получим
|
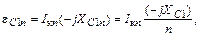
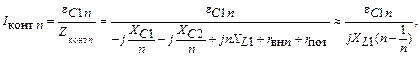
так как волновое сопротивление контура
|
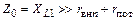 ,
,
поскольку контур высокодобротный.
Далее
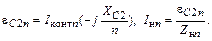
|
|
В результате имеем
|
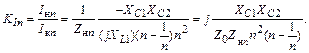
Коэффициент фильтрации определяется модулем соответствующих отношений, поэтому
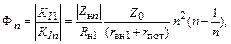
|
где Q = 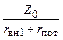 − нагруженная добротность контура.
− нагруженная добротность контура.
Тогда коэффициент фильтрации П-контура 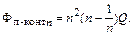
В результате для обеспечения требуемого коэффициента фильтрации (1.58) получаем
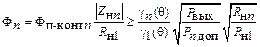
или
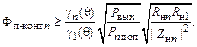 (1.65)
(1.65)
Рассмотрим следующий пример.
Исходные данные:
Pвых = 20 Вт; Pn доп = 1мВт; 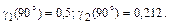
Сопротивления Rн1, |Zнn| и Rнn могут значительно различаться, но для простоты оценки положим их равными, тогда
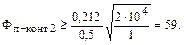
Коэффициент фильтрации при n = 2
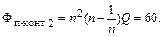
|
Следовательно, 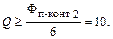
Возникает вопрос: какую добротность контура следует выбрать? Чем выше Q, тем лучше фильтрация, но тем уже полоса пропускания (см. расчет схемы 1.3) и тем больше потери мощности в контуре.
Коэффициент полезного действия контура
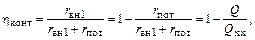 (1.66)
(1.66)
где 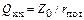 − собственная добротность контура (добротность холостого хода).
− собственная добротность контура (добротность холостого хода).
Величину Qxx определяет граница, при которой обеспечивается фильтрация. Если величина Q оказывается большой и КПД контура падает ниже 80%, то для фильтрации гармоник используют более сложные колебательные системы, чем П-контур.
Дата добавления: 2016-01-07; просмотров: 3014;
