Квадратурный мост на связанных линиях
На участках a-b и a′-b′ две линии длиной 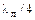 имеют между собой электромагнитную связь (рис. 1.33). Если в системе Rн = Rбал = Z0, то точки, расположенные на диагоналях a-a′ и b-b′, развязаны между собой.
имеют между собой электромагнитную связь (рис. 1.33). Если в системе Rн = Rбал = Z0, то точки, расположенные на диагоналях a-a′ и b-b′, развязаны между собой.
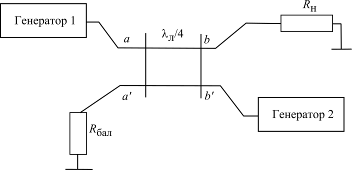
Рис. 1.33. Квадратурный мост на связанных линиях
Мощность каждого генератора в отсутствие другого делится поровну между Rн и Rбал. При этом напряжение в точке a′ Ген 1 будет синфазно с выходным напряжением Ген 1, а напряжение в точке b будет отставать по фазе на 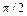 . Аналогично, напряжение в точке a′ отстает на
. Аналогично, напряжение в точке a′ отстает на 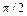 по фазе от напряжения Ген 2, а в точке b синфазно с ним. Чтобы мощности обоих генераторов суммировать в нагрузке, фаза выходного напряжения Ген 1 должна на
по фазе от напряжения Ген 2, а в точке b синфазно с ним. Чтобы мощности обоих генераторов суммировать в нагрузке, фаза выходного напряжения Ген 1 должна на 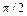 опережать фазу напряжения Ген 2. В балласте при этом ничего не выделяется. Если балласт и нагрузку поменять местами, то фазовые соотношения между напряжениями Ген 1 и Ген 2 следует инвертировать. Достаточно подробно теория работы этого моста рассмотрена в [5].
опережать фазу напряжения Ген 2. В балласте при этом ничего не выделяется. Если балласт и нагрузку поменять местами, то фазовые соотношения между напряжениями Ген 1 и Ген 2 следует инвертировать. Достаточно подробно теория работы этого моста рассмотрена в [5].
Автогенераторы и стабилизация частоты
Общие замечания
Главное назначение автогенераторов (АГ) – генерация высокочастотных колебаний радиочастоты. Важнейшей характеристикой АГ является нестабильность частоты. На частоту влияет множество факторов: температура, питающие напряжения, давление воздуха, старение деталей, шумы транзисторов, воздействие внешних излучений (наводки). Поэтому частота автоколебаний есть величина случайная.
При измерениях получают усредненное значение частоты:
|
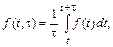 (2.1)
(2.1)
где τ – время измерений.
Результат измерений зависит не только от интервала измерений τ, но и от текущего времени t.
При оценке нестабильности частоты используют понятия долговременной и кратковременной нестабильности. Долговременную нестабильность частоты оценивают за разные интервалы времени (год, месяц, сутки, часы). При оценке кратковременной нестабильности время усреднения надо сократить до долей секунды, но чем оно меньше, тем больше погрешности измерений. Поэтому при оценке кратковременной нестабильности частоты широко используют спектральный метод.
Дисперсия отклонения угловой частоты 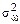 связана с энергетическим спектром АГ соотношением:
связана с энергетическим спектром АГ соотношением:
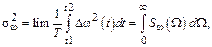 (2.2)
(2.2)
где 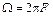 – угловая частота воздействующего на АГ дестабилизирующего фактора (помехи), а для математической строгости следует принять
– угловая частота воздействующего на АГ дестабилизирующего фактора (помехи), а для математической строгости следует принять 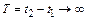 .
.
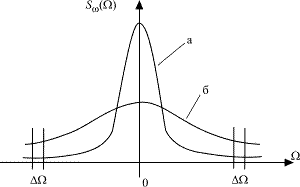
Рис. 2.1. Энергетические спектры колебания АГ
Это сплошной спектр (рис. 2.1), на который могут быть наложены отдельные спектральные составляющие. Каждый участок спектра полосой ΔΩможно рассмотреть как результат воздействия дестабилизирующего фактора, приводящего к паразитной частотной модуляции. Кратковременную нестабильность частоты оценивают по ширине спектральной линии АГ. Чем она уже (кривая «а» в сравнении с кривой «б»), тем меньше величина кратковременной нестабильности частоты [4].
В нормативных документах на АГ указывают допустимый уровень спектральных составляющих, отстоящих от центральной частоты на различные значения F.
Требования к стабильности частоты в приемопередатчиках базовых и абонентских станций систем подвижной связи весьма жесткие. Допустимая относительная нестабильность частоты находится на уровне 10–6…10–7, поэтому при анализе процессов, вызывающих нестабильности частоты, приходится считаться со множеством малозаметных факторов.
2.2. Автогенераторы. Основные схемы
и соотношения стационарного состояния
В схемах АГ существует положительная обратная связь между выходом и входом схемы, а в стационарном состоянии выполняются определенные условия баланса. Простейшими схемами АГ являются емкостная и индуктивная трехточки (рис. 2.2).
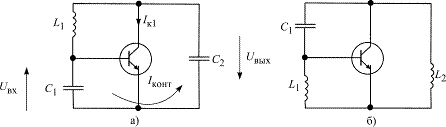
Рис. 2.2. Эквивалентные схемы АГ:
а – емкостная и б – индуктивная трехточки
Частоту АГ задает колебательный контур. В схеме емкостной трехточки (рис. 2.2, а) – это конденсаторы С1, С2 и индуктивность L1, в схеме индуктивной трехточки (рис. 2.2, б) – две индуктивности L1, L2 и конденсатор С1. Контура имеют большую добротность (от нескольких десятков до 200). В контуре протекает контурный ток İконт, значительно превосходящий токи выводов транзистора. Частота автоколебаний мало отличается или равна резонансной (собственной) частоте колебательной системы.
Для емкостной трехточки:
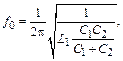 (2.3)
(2.3)
для индуктивной

|
|
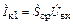 , (2.5)
, (2.5)
где 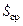 – средняя крутизна транзистора по первой гармонике.
– средняя крутизна транзистора по первой гармонике.
На контуре возникает напряжение первой гармоники
 (2.6)
(2.6)
|
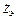 – эквивалентное сопротивление нагрузки.
– эквивалентное сопротивление нагрузки.
При этом вектор 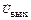 направлен в противоположную сторону по отношению вектору тока
направлен в противоположную сторону по отношению вектору тока 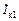 .
.
Протекающий в контуре ток создает по цепи обратной связи (емкости С1 и С2) напряжение на входе [7]:
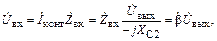
|
где 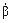 – коэффициент обратной связи, а
– коэффициент обратной связи, а  – эквивалентное входное сопротивление между точками б-э транзистора.
– эквивалентное входное сопротивление между точками б-э транзистора.
Подставив Ùвх (2.7) в (2.5) и заменив Ùвых выражением (2.6), получим уравнение стационарного состояния АГ:

|
Все три величины в (2.8) комплексные, все они могут давать фазовые сдвиги φS, φβ, φZ.
Выражение (2.8) разделяется на два уравнения баланса:
амплитуд
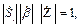
|
фаз
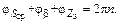 (2.10)
(2.10)
В большинстве схем АГ n = 0, так что 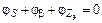 . Уравнение баланса фаз АГ определяет частоту автоколебаний, а уравнение баланса амплитуд – их амплитуду.
. Уравнение баланса фаз АГ определяет частоту автоколебаний, а уравнение баланса амплитуд – их амплитуду.
Если в схеме рис. 2.2, а принять 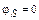 (фазовые сдвиги в транзисторе отсутствуют или скомпенсированы), а также считать входное сопротивление транзистора гораздо больше ХС1, то
(фазовые сдвиги в транзисторе отсутствуют или скомпенсированы), а также считать входное сопротивление транзистора гораздо больше ХС1, то 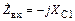 и
и 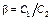 . Следовательно,
. Следовательно, 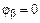 и согласно уравнению баланса фаз
и согласно уравнению баланса фаз 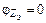 . В этом случае, когда
. В этом случае, когда 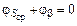 ,частота автоколебаний АГ совпадает с собственной частотой его контура.
,частота автоколебаний АГ совпадает с собственной частотой его контура.
АГ – нелинейные устройства. Чтобы в них установились автоколебания, транзисторы должны работать в нелинейном режиме (обычно в районе нижнего загиба статических характеристик). В уравнении баланса амплитуд 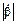 и
и 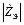 определяются линейными элементами схемы и они не зависят от амплитуды колебаний [2,7]. Средняя крутизна
определяются линейными элементами схемы и они не зависят от амплитуды колебаний [2,7]. Средняя крутизна 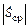 зависит от амплитуды
зависит от амплитуды 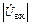 . Для устойчивой работы АГ
. Для устойчивой работы АГ 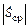 должна падать с ростом амплитуды
должна падать с ростом амплитуды 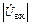 (рис. 2.3), где
(рис. 2.3), где 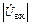 в стационарном состоянии обозначено как
в стационарном состоянии обозначено как 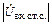 .
.
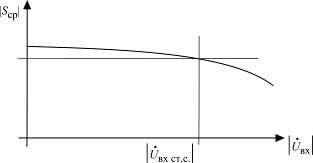
Рис. 2.3. Зависимость 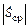 от
от 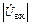
Спад 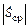 обеспечивает автоматическое смещение на базе транзистора АГ.
обеспечивает автоматическое смещение на базе транзистора АГ.
Один из возможных вариантов схемы емкостной трехточки приведен на рис. 2.4, а его эквивалентная схема на рис. 2.4, б.
В этой схеме по радиочастоте заземлен коллектор (блокирующий конденсатор Сбл2 имеет большую емкость, теоретически его сопротивление должно быть нулевым). Сопротивления R1 и R2 образуют делитель в цепи подачи напряжения смещения на базу. Резистор R3 – сопротивление автоматического смещения в цепи эмиттера. Lбл и Сбл1 образуют блокирующий фильтр в коллекторной цепи. Вообще в схеме АГ по радиочастоте с корпусом может быть соединен любой вывод транзистора.
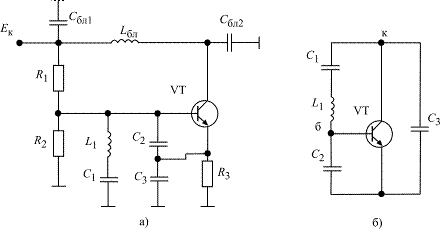
Рис. 2.4. Схема АГ (емкостная трехточка): а – электрическая, б – эквивалентная
Цепь С3R3 и резистивный делитель R1R2 с параллельно подключенными емкостями обеспечивают инерционное изменение смещения на базе от Еб1 до Еб2 (рис. 2.5). Тем самым с ростом амплитуды изменяется средняя крутизна.
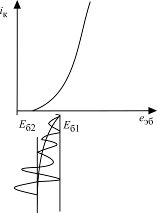
Рис. 2.5. Процесс управления амплитудой в АГ
Обратим внимание на то, что между коллектором и базой стоит не просто индуктивность, а цепочка L1C1. Это необходимо для согласования характеристик контура с параметрами транзистора.
Пример расчета АГ. Рассчитать элементы колебательной системы АГ, построенного по схеме (рис. 2.4, а), со следующими исходными данными:
частота АГ 430 МГц,
амплитуда напряжения радиочастоты на коллекторе 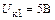 ,
,
ток коллектора Iк1 = 8 мА,
коэффициент обратной связи β = 0,25,
характеристическое сопротивление контура Z0 = 30…100 Ом. 80 < Q ≤ 100.
1. Определим сопротивление коллекторной нагрузки:
RЭ1 = UК1 / I K1= 5/(8·10–3) = 625 Ом.
|
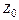 и Q, которые берут из конструктивных соображений в указанных пределах. Возьмем
и Q, которые берут из конструктивных соображений в указанных пределах. Возьмем 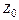 = 60 Ом (попробуйте сделать расчет при
= 60 Ом (попробуйте сделать расчет при 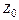 = 30 и 120 Ом). Добротность для наибольшей стабилизации частоты следует увеличить. Возьмем Q = 100, тогда эквивалентное сопротивление контура при его полном включении (рис. 2.6)
= 30 и 120 Ом). Добротность для наибольшей стабилизации частоты следует увеличить. Возьмем Q = 100, тогда эквивалентное сопротивление контура при его полном включении (рис. 2.6)
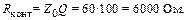
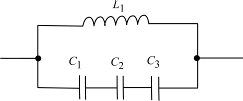
Рис. 2.6. Эквивалентная схема контура АГ
3. Коэффициент подключения контура к транзистору определим из соотношения 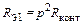 :
:
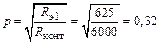 .
.
4. Найдем сопротивление конденсатора С3:
XС3 = p·Z0 = 0,32·60 = 19,2 Ом.
5. Сопротивление конденсатора С2:
XC2 = β·XC3 = 0,25·19,2 = 4,8 Ом.
6. Сопротивление конденсатора С1:
XC1 = Z0 – XC2 – XC3 = 60 – 19,2 – 4,8 = 36 Ом.
Далее следует самостоятельно рассчитать величины конденсаторов и индуктивностей схемы, а также ток в контуре.
2.3. Основное уравнение нестабильности частоты
и методы стабилизации
Частоту АГ определяют из уравнения баланса фаз (2.10). Пусть ω – угловая частота АГ при значении некоторого дестабилизирующего фактора  (например, температуры).
(например, температуры).
В соответствии с (2.10):
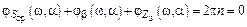
|
При изменении дестабилизирующего фактора  на Δ
на Δ  , частота ω изменяется наΔω. Уравнение баланса фаз должно выполняться при любой частоте АГ, поэтому
, частота ω изменяется наΔω. Уравнение баланса фаз должно выполняться при любой частоте АГ, поэтому
 (2.12)
(2.12)
Поскольку отклонения Δωи Δ  малы, после разложения в ряд Тэйлора каждого из слагаемых (2.12) получим:
малы, после разложения в ряд Тэйлора каждого из слагаемых (2.12) получим:

или
 . (2.13)
. (2.13)
Уравнение (2.13) называют основным уравнением нестабильности частоты АГ. Проанализируем его.
Знаменатель уравнения (2.13) есть фиксирующая способность АГ.
Обратим внимание на то, чтоφScp и φβ при малых уходах частоты практически не меняются, поэтому можем принять
|
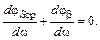
Напротив, 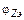 определяется резонансным элементом – контуром.
определяется резонансным элементом – контуром.
Так как
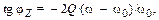
|
где ω0 – резонансная частота контура, то
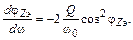
|
Частоты ωи ω0 всегда очень близки, поэтому
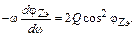
|
Преобразуем уравнение (2.13):
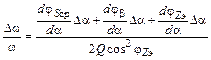 . (2.17)
. (2.17)
Обратимся к числителю выражения (2.17).
Из-за воздействия дестабилизирующего фактора  меняются собственная частота контура ω0 и его добротность Q, тогда:
меняются собственная частота контура ω0 и его добротность Q, тогда:
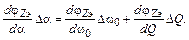 (2.18)
(2.18)
Дифференцируя (2.14), получаем:
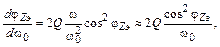 (2.19)
(2.19)
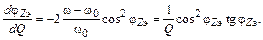 (2.20)
(2.20)
Обозначив

и подставив (2.18), (2.19) и (2.20) в (2.17), получим окончательно:
|
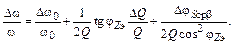 (2.21)
(2.21)
Выражение (2.21) весьма удобно для инженерного анализа. Первое и самое главное: частота автоколебаний строго следует за собственной (резонансной) частотой контура. Если величина ω0 изменится на Δω0, то практически так же меняется и частота ω. Невозможно никаким увеличением добротности Q снизить уход частоты АГ при изменении ω0. Значит важнейшей задачей при создании высокостабильных АГ является стабилизация собственной частоты его контура. Элементы контура зависят от температуры, питающих напряжений (емкости транзистора), поэтому термостабилизирование всей схемы АГ и стабилизация питающих напряжений является обязательным условием достижения высокой стабильности частоты АГ.
Что касается изменения добротности, оно мало влияет на частоту, а если ω = ω0, то и совсем не влияет, так как при этом  .
.
Наконец, изменение фазовых углов средней крутизны и коэффициента обратной связи 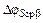 из-за фазовых сдвигов внутри транзистора и ряда других факторов компенсируются изменением с обратным знаком углом φZэ, так что
из-за фазовых сдвигов внутри транзистора и ряда других факторов компенсируются изменением с обратным знаком углом φZэ, так что 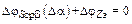 . При этом уход частоты тем меньше, чем больше добротность контура Q. Все сказанное можно проиллюстрировать на фазовых характеристиках АГ (рис. 2.7).
. При этом уход частоты тем меньше, чем больше добротность контура Q. Все сказанное можно проиллюстрировать на фазовых характеристиках АГ (рис. 2.7).
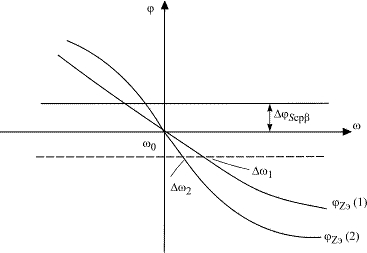
Рис. 2.7. Установление баланса фаз при изменении фазовых углов  и
и 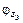
На рис. 2.7 отклонение 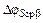 скомпенсировано
скомпенсировано 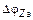 . При низкой добротности контура Q уход частоты от ω0 составляет Δω1; при увеличении Q уход частоты Δω2 значительно меньше. Если же уходит собственная частота контура ω0, за ней будет следовать и частота автоколебаний ω. Для стабилизации частоты ω0 широко используют кварцевые резонаторы.
. При низкой добротности контура Q уход частоты от ω0 составляет Δω1; при увеличении Q уход частоты Δω2 значительно меньше. Если же уходит собственная частота контура ω0, за ней будет следовать и частота автоколебаний ω. Для стабилизации частоты ω0 широко используют кварцевые резонаторы.
Дата добавления: 2016-01-07; просмотров: 2441;
