Построение разверток кривых развертывающихся поверхностей
Развертки всех развертывающихся кривых поверхностей являются приближенными. Это объясняется тем, что кривые поверхности приближенно заменяют (аппроксимируют) поверхностями вписанных или описанных многогранников с гранями в виде треугольников или четырехугольников. С этой точки зрения конус можно заменить пирамидой, а цилиндр – призмой. Поэтому приемы построения разверток линейчатых кривых и гранных поверхностей аналогичны, с той лишь разницей, что вместо ребер на кривой поверхности проводят достаточное число образующих.
На рисунке 89 показано построение развертки прямого кругового цилиндра. Развертка его боковой поверхности – прямоугольник, одна сторона которого равна длине окружности основания ПD, а другая высоте цилиндра Н.
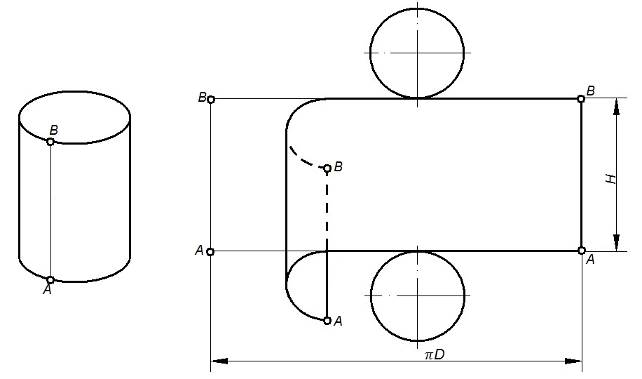
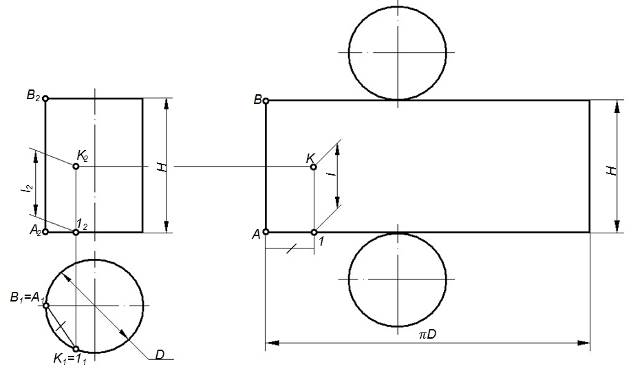
Рисунок 89 – Развертка цилиндра
В том случае, когда многогранная поверхность, заменяющая кривую поверхность, имеет треугольные грани, способ построения развертки называется способом триангуляции (треугольников).
На рисунке 90 построена развертка боковой поверхности усеченного конуса.
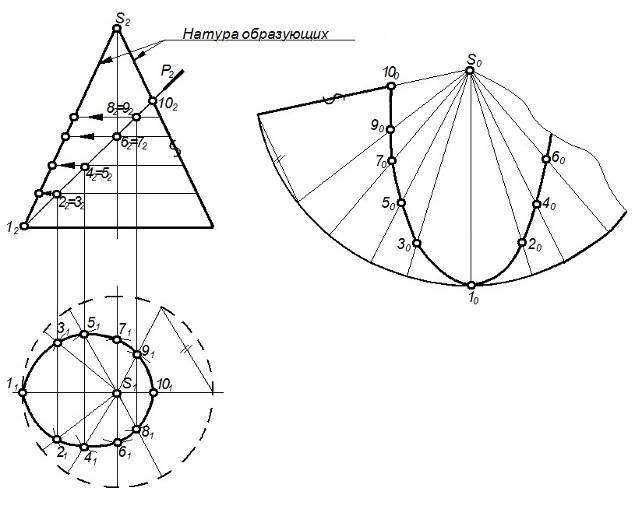
Рисунок 90 – Развертка конуса
Поверхность конуса заменена поверхностью пирамиды, вписанной в конус.
Натуральную величину образующих определяем, переместив все образующие и отрезки на них в положение крайней образующей, которая расположена параллельно фронтальной плоскости проекций.
Список литературы
1. Н.П. Сенигов, Т.В. Гусятникова, Н.В. Ларионова, В.С. Дукмасова, А.М. Швайгер Начертательная геометрия. – Челябинск: Издательство ЮУрГУ, 2000.
2. С.А. Фролов Начертательная геометрия. – М.: Машиностроение, 1991.
3. Бубенников А.В. Начертательная геометрия. – М.: Высшая школа, 1985
4. А.А. Чекмарев Инженерная графика – М.: Высшая школа, 1985
5. В.С. Дукмасова, В.А. Краснов Методика решения задач по начертательной геометрии. – Челябинск: Издательство ЮУрГУ, 2003
6. С.В. Евсеенков, Л.С. Хазанская Методические изучения к изучению курса начертательной геометрии – Челябинск: Издательство ЧГАУ, 1991
7. Ж.В. Путина, Л.И. Хмарова, Э.М. Зорина Подготовка к защите контрольных графических заданий по начертательной геометрии – Челябинск: Издательство ЮУрГУ, 2000
Дата добавления: 2016-01-07; просмотров: 1962;
