П Р И Л О Ж Е Н И Е

(Варианты заданий и примеры их выполнения)

1 Общие требования к выполнению домашних контрольных работ

В процессе изучения курса начертательной геометрии, в соответствии с учебным планом, студенты должны выполнить четыре домашние контрольные работы. Это необходимо для того, чтобы студент усвоил пройденный материал и умел применять правила и приемы начертательной геометрии при решении определенных практических задач.

Номер варианта контрольной работы соответствует последней цифре зачетной книжке студента.

Работа № 1 - Пересечение плоскостей (выполняется на формате А4)

Работа №2 - Сечение плоскостью (формат А3)

Работа №3 - Пересечение двух поверхностей (формат А3)

Работа №4 - Пересечение двух тел вращения (формат А3)

Чертежи контрольных работ выполняются на отдельных листах чертежной бумаги формата А4 (210х297 мм) и формата А3 (297х420 мм) На каждом листе вычерчивается рамка и на формате А3 в правом нижнем углу чертежа выполняется основная надпись (штамп) по ГОСТ 2104-94 (рисунок 1, 2). На формате А4 штамп располагается внизу чертежа, вдоль короткой стороны (рисунок 1).

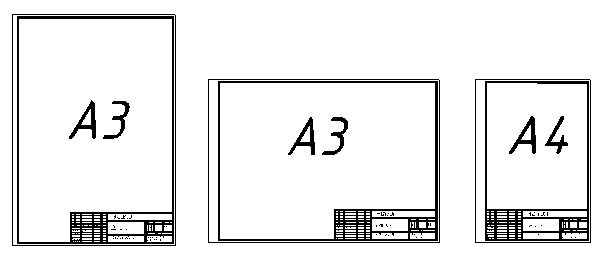
Рисунок 1 – Применяемые форматы для выполнения работ

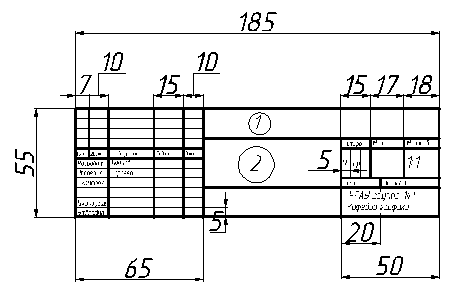
Рисунок 2 – Основная надпись формата

После выполнения всех работ они брошюруются в альбом с титульным листом формата А3 (рисунок 3) Размеры при выполнении титульного листа не указываются.

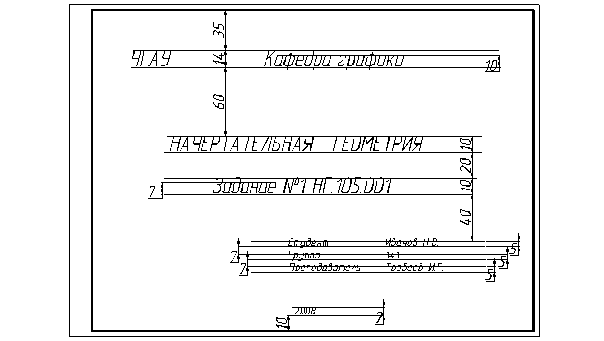
Рисунок 3 – Титульный лист задания

Альбом контрольных работ сдается студентом на проверку преподавателю - экзаменатору.

При заполнении основной надписи (штампа) необходимо учесть следующее:

1) Графа 1(рисунок 2) заполняется следующим образом НГ.105.001, где НГ - начертательная геометрия, первая цифра - № задания, вторая и третья цифры - № варианта, три оставшиеся цифры - № работы.

2) В графе 2 (рисунок 2) записывается название работы (названия работ перечислены ранее)

2. Рекомендации к выполнению контрольной работы №1

Изучив теоретический материал, можно приступить к выполнению домашних контрольных работ. Содержание контрольной работы №1: даны точки В, С, D, E, F, своими координатами вычисленные по отношению точки А(А1,А2) (таблица 1). Координаты точки А - произвольные. Проекции точки А (А1А2) нужно брать так, чтобы длина линии связи была не меньше чем

А1А2 =[-Ymax]+[-Zmax]+10. Требуется построить прямую линию пересечения между плоскостями ABC и DEF и определить их видимость по отношению плоскостей проекций П1 и П2.

Задача решается на формате А4 (образец выполнения этой работы на рис. 4). Проекции точек B, C, D, E, F, строят по координатам (табл. 1), заданным относительно точки А.

После решения задачи видимые части треугольников можно раскрасить цветными карандашами.

Для решения задачи необходимо сначала проанализировать заданный чертеж. Плоскости, заданные треугольниками ABC и DEF, - общего положения. Следовательно, эта задача третьей группы сложности. Из теории должно быть известно, что такие задачи решаются при помощи посредников. Каждый посредник помогает выявить одну общую точку. Необходимо построить линию пересечения, т.е. не менее двух точек,

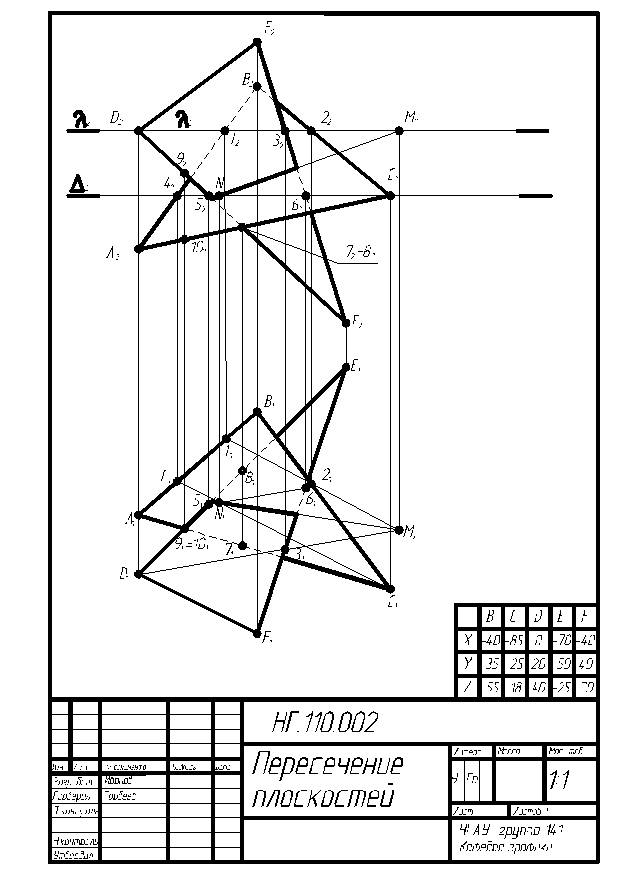
Рисунок 4 – Пример выполнения задания №1

следовательно, и посредников должно быть два. Рассмотрим решение на примере (рис. 4)

1.Пересечем заданные плоскости ABC и DEF вспомогательной плоскостью - посредником λ(λ2) (горизонтальной плоскостью уровня) и далее строим линии пересечения плоскости λ с каждой из данных плоскостей: λ Ç ABC=1,2; λ Ç DEF=D,3. Так как λ ^ П2, то 1222=λ2 и D232=λ2 Горизонтальные проекции точек 1,2 и 3 строим на основании принадлежности: 1 с АВ, 2 с ВС и 3 с EF.

2.Находим точку пересечения построенных прямых на горизонтальной плоскости проекций 1121 Ç D131=M1. Т.к. точка М принадлежит плоскости λ, то вторую проекцию точки M (М2) строим на основании принадлежности λ(λ2). Точка M принадлежит трем плоскостям ABC, DEF и λ, следовательно, она является первой точкой, принадлежащей линии пересечения.

3.Для того чтобы найти еще одну точку аналогично, проведем вторую вспомогательную плоскость D(D2) (горизонтальную плоскость уровня) : D Ç ABC=C,4; D Ç DEF=5,6.

Так как D ||λ, то нет необходимости находить горизонтальные проекции всех точек. Достаточно найти горизонтальную проекцию точки 5 и провести 5161 || D131 и С141||1121 Там где C141 и 5161 пересекутся, находится вторая точка N (N1,N2), N2 находится аналогично M2.

4.Соединив M1N1 и N2M2, получим проекцию линии пересечения.

5.Видимость определяем при помощи конкурирующих точек. На П2 конкурирующие точки 72=82 выбираем в месте видимого пересечения E2F2 и A2B2. Из точек 7₂ =8₂ опускаем линию связи на П₁. Точки 7EF, точка 8AB на П1 видим, что точка 7 находится ближе, чем точка 8. Делаем вывод, что в месте видимого пересечения видимой является E2F2 . Аналогично на П1 конкурирующие точки 91=101, 9BC, 10FE. По линии связи определяем, что точка 9 находится выше, чем 10, следовательно, видимой является B1C1. Без определения видимости задача считается нерешенной.

3 Рекомендации к выполнению контрольной работы №2

Содержание контрольной работы №2: дано непрозрачное комплексное тело (таблица 2). Фронтально-проецирующую секущую плоскость Р(Р2), проводим самостоятельно через середину высоты комплексного тела под углом 60° к горизонтальной плоскости проекций.

Требуется построить проекции и определить натуральную величину сечения поверхности комплексного тела секущей плоскостью способом замены плоскостей проекций и способом плоскопараллельного перемещения.

Плоскость, секущая геометрическое тело, считается непрозрачной и безграничной. Исходя из этого, нужно определить видимость элементов

геометрического тела на П1. Секущая плоскость получится видимой на П2 в виде прямой линии.

Исходный чертеж исполняется в масштабе 1:1 на листе чертежной бумаги формата А3 Выполненную работу в тонких линиях предъявить на проверку преподавателю, после чего можно проекции сечения и натуральную величину сечения обвести цветными карандашами.

Решение задачи рассмотрим на примере (рисунке 5). Фронтальная проекция сечения вырождается в прямую линию, совпадающую с проекцией фронтально-проецирующей плоскостью Р(Р2). Следовательно, строить нужно горизонтальную проекцию сечения. Для этого разбиваем фронтальную проекцию на вспомогательные точки, по которым и будем строить горизонтальную проекцию сечения. Определим сначала высшие точки (1,2) и низшие (9,10). Высшие точки лежат на очерке призмы, низшие - на плоскости основания шаровой поверхности. Таким образом, найти горизонтальные проекции нетрудно, достаточно опустить линии связи до пересечения; для точек 1 и 2 - с очерком призмы; для точек 9 и 10- с нижним основанием шаровой поверхности. Далее определяем точки 3 и 4 - эти точки расположены на ребрах призмы.

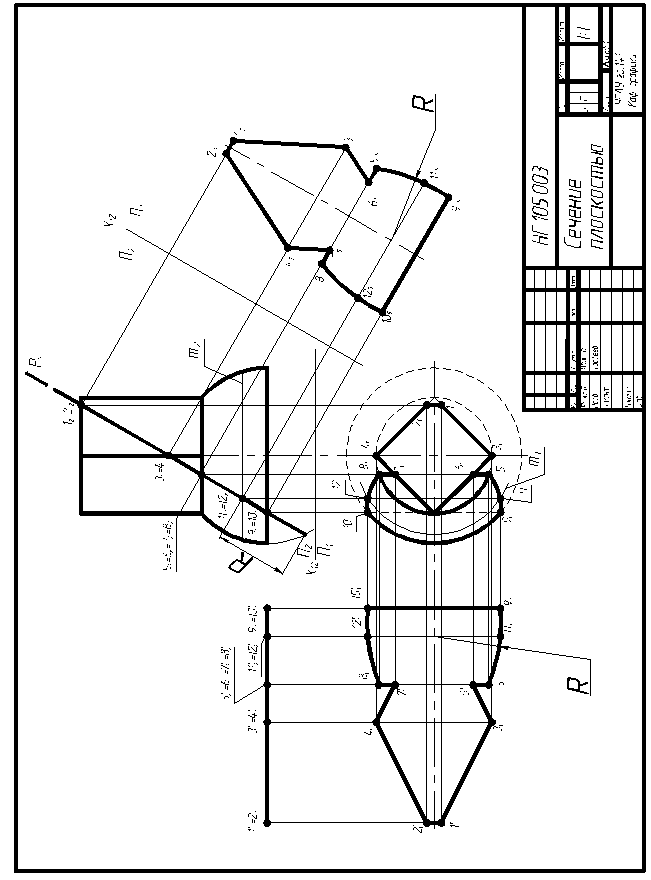
Рисунок 5 – Пример выполнения задания №2

Следующие точки 5,6,7,8 - они расположены в месте перехода шаровой поверхности в поверхность призмы. Точки 5 и 8 лежат на верхнем основании усеченной шаровой поверхности, а точки 6 и 7 - на основании призмы.

Случайные точки 11 и 12 находим при помощи параллели m (m2). Для этого на П1 радиусом параллели R (радиус определяется от оси до очерка) строим горизонтальную проекцию параллели m (m1) и находим при помощи линий связи находим на ней горизонтальные проекции точек 11 и 12.

Полученные точки на П1 соединяем с учетом видимости, считая Р бесконечной и непрозрачной. Тогда при взгляде на П1 правая часть комплексного тела будет находиться под плоскостью Р и, следовательно, будет невидима на П1.

Следующим этапом решения задачи является определение натуральной величины сечения. Сначала рассмотрим способ замены плоскостей проекций. Плоскость проекций П1 заменяем на П5, причем располагаем П5 параллельно сечению. Для этого на чертеже необходимо провести ось Х12 (можно провести ее по низу фигуры) и новую ось Х25, которая должна быть параллельна Р2. Расстояние между Р2 и Х25 берется произвольно, исходя из соображений компактности чертежа. Поскольку расстояния до незаменяемой плоскости проекций П₂ сохраняются на П5, их замеряют на П1 (от точки до оси Х12)и откладываются на соответствующей линии связи на П5 (от оси Х25). Полученные точки соединяются линией.

Теперь рассмотрим способ плоскопараллельного перемещения. В этом случае фронтальную проекцию сечения расположим параллельно оси Х12 (сохраняя при этом расстояние между точками неизменным). Для получения натуральной величины теперь достаточно провести линии связи от каждой точки с П2 и с П1. В месте пересечения одноименных линий

связи получатся точки натуральной величины сечения. Полученные точки соединяются линией.

Следует обратить внимание на следующее:

1. Поскольку натуральную величину необходимо получить двумя способами, компоновку чертежа нужно стараться делать так же, как на образце (рисунок 5)

2. В обоих случаях фигура натуральной величины сечения должна получиться одинаковой.

4 Рекомендации к выполнению контрольной работы №3

Содержание работы №3: способом вспомогательных секущих плоскостей, или по принадлежности точек к одному из геометрических тел, построить линию взаимного пересечения поверхностей заданных геометрических тел (таблица 3). Определить видимость.

При определении точек линии пересечения между поверхностями заданных геометрических тел, в первую очередь обязательно находятся и обозначаются на чертеже характерные (опорные) точки: экстремальные (высшая и низшая, передняя и задняя, левая и правая), очерковые точки для каждой поверхности и на каждой проекции, а также точки, расположенные на ребрах многогранника, и точки смены видимости.

Количество произвольных точек должно быть достаточным для построения плавной кривой линии или ломаной кривой линии пересечения.

Рассмотрим решение задачи на примере (рисунок 6). Первое, что нужно сделать, это проанализировать чертеж. Итак, пересекаются две фигуры: пирамида и цилиндр, т.е. поверхность вращения с многогранником. Следовательно в результате пересечения должна получиться ломаная кривая линия. Поскольку ни одна из фигур не участвует полностью в пересечении, это значит, что мы имеем дело со случаем врезки, а это в свою очередь значит, что линией пересечения будет одна замкнутая ломаная кривая линия. Теперь сами фигуры: пирамида - фигура общего положения, цилиндр - фронтально проецирующий, поскольку ось цилиндра перпендикулярна фронтальной плоскости проекции. Задача второй группы сложности. Проецирующие фигуры обладают собирательным свойством: все точки на поверхности фигуры (в том числе и линия пересечения) совпадают с главной (вырожденной) проекцией этой фигуры. В нашем случае линия пересечения совпадает с фронтальной проекцией цилиндра, т.е. с окружностью на П2. Теперь, для того чтобы построить линию пересечения на П1, мы разобьем окружность на точки и будем строить эти точки на П1 на основании принадлежности к пирамиде.

Выберем опорные точки: 1 и 2 - точки, лежащие на ребрах пирамиды и одновременно самые левые; 3 и 4 - эти точки также лежат на ребрах пирамиды и одновременно самые верхние; 5 и 6 - точки, лежащие на оси цилиндра, следовательно, это точки смены видимости, кроме того это самые правые точки; 7 и 8 – это самые нижние точки и так как они лежат на оси цилиндра, то точка 7 - самая ближняя, точка 8 - самая дальняя.

Теперь случайные точки: для построения точек 7 и 8 проведем вспомогательные линии, т.е. соединим вершину пирамиды S с точками 7 и 8 и найдем, где эти линии пересекут основание пирамиды в точках M и N. Эти вспомогательные линии на П2 кроме точек 7 и 8 пересекают окружность еще в одном месте, там мы обозначим случайную пару точек 9 и 10.

Далее произвольно проведем параллель ниже точек 1 и 2, но выше точек 7 и 8, на этой параллели возьмем две пары случайных точек 11 и 12, а также 13 и 14. Последнюю пару случайных точек 15 и 16 также возьмем при помощи параллели, которую проведем ниже точек 9 и 10 и выше 5 и 6.

Следующий шаг: отыщем эти точки на П1. Точки 1, 2, 3 и 4 лежат на ребрах пирамиды (1 и 3 на SA, 2 и 4 на SB), поэтому для определения достаточно провести линии связи. Как найти точки 7, 8, 9 и 10 описано выше. Для отыскания остальных точек были проведены параллели на П2, далее параллели построены на П1 и при помощи линии связи найдены искомые точки. Все точки найдены. Они соединяются в ломаную кривую линию. Точки 5 и 6 на линии пересечения являются точками смены видимости. Вся линия пересечения, которая на П2 расположена выше точек 5 и 6, на П1 видима.

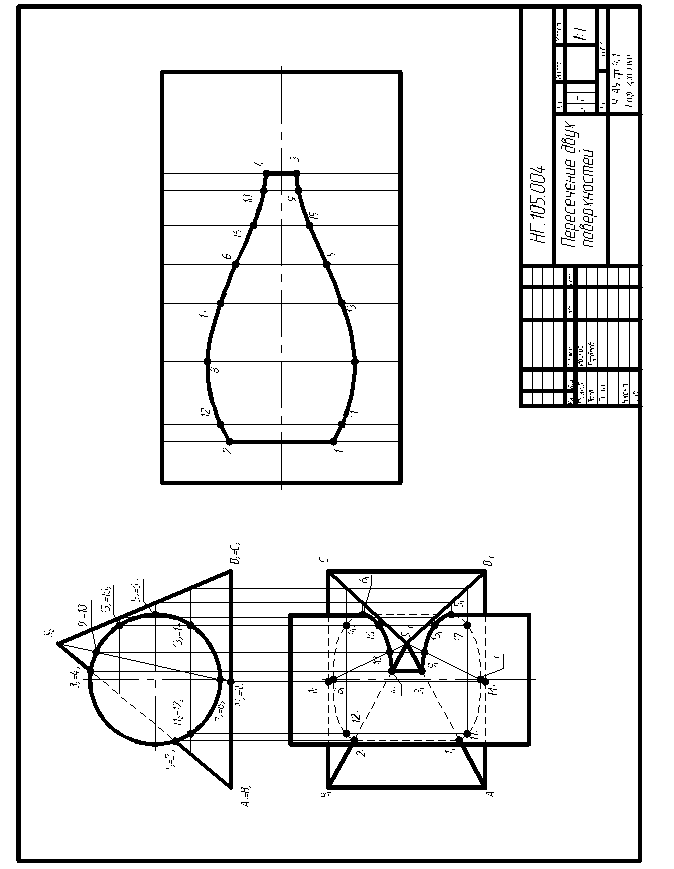
Рисунок 6 – Пример выполнения задания №3

Последнее, что необходимо сделать, это определить видимость в видимом контуре цилиндра и пирамиды. На П2 не видимыми в контуре пирамиды являются часть ребер SA и SB между точками 1, 3 и 2, 4. На П1 весь очерк цилиндра видим, кроме части между точками 5 и 6. Часть основания пирамиды невидима, т.к. находится ниже цилиндра. Невидимы также части ребер SA и SB, начиная от точек 3 и 4 и до очерка цилиндра. Напомним, что работа выполняется на формате А3 по действительным размерам в масштабе 1:1. Чертеж выполняется в двух проекциях, за исключением тех вариантов, где указано выполнить работу в трех проекциях.

4 Рекомендации к выполнению контрольной работы №4

Содержание контрольной работы №4: способом вспомогательных концентрических сфер построить линию взаимного пересечения поверхностей двух тел вращения (таблица 4). Определить видимость (образец выполнения задачи рисунок 7).

Рассмотрим применение этого способа на примере (рисунок 7).

Даны две фигуры вращения: конус и закрытый тор. Фигуры имеют одну общую плоскость симметрии λ(λ1), которая является фронтальной плоскостью уровня (т.е. ^ П1, || П2). Оси симметрии, вокруг которых происходит вращение образующих линий фигур, пересекаются в точке О (О2) под углом 90° . Таким образом, на лицо все признаки применения способа концентрических сфер.

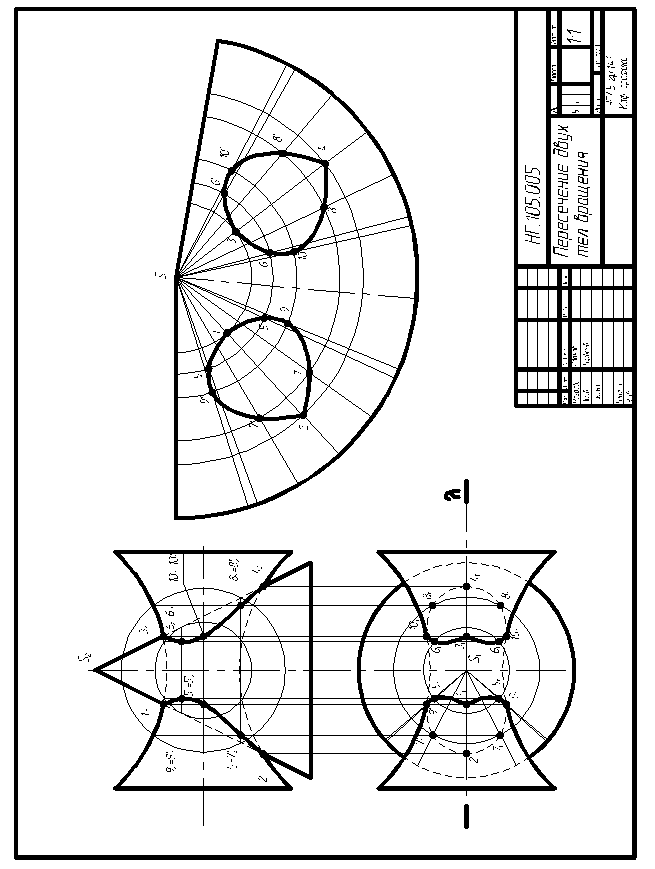
Рисунок 7 – Пример выполнения задания №4

В данном примере общая плоскость симметрии λ(λ1) П2. Поэтому высшие и низшие точки линии пересечения 1;3 и 2;4 получаются непосредственно в пересечении очерковых образующих. Все четыре точки легко определить на фронтальной плоскости проекций.

Все остальные точки линии пересечения находим с помощью вспомогательных сфер, которые будем проводить из точки О (О2) - точки пересечения осей конуса и цилиндра. Причем, при нахождении точек пересечения следует помнить, что в данном случае мы имеем дело с проницанием, а это значит, что линий пересечения получится две, и так как фигуры расположены симметрично относительно друг друга, линии пересечения должны получиться также симметричными. Сферой наименьшего радиуса является сфера, вписанная в поверхность одного из пересекающихся тел. С поверхностью другого тела такая сфера должна пересекаться. В данном примере такая сфера вписывается в конус и пересекается с тором. Для того, чтобы определить радиус этой сферы, из точки О(О1) на очерковую образующую линию опущен перпендикуляр. Эта сфера является соосной с поверхностью обоих тел, и потому она касается поверхности конуса и пересекается с поверхностью тора по окружностям, которые проецируются на фронтальную плоскость проекций в виде прямых линий. Так как эти окружности принадлежат одной сфере, то они пересекаются в двух парах точек 5(52), 5'(52') и 6(62), 6' (62'), которые являются общими между поверхностями конуса и тора, а следовательно, располагаются на линии пересечения. Произвольные точки 7(72), 7'(72') и 8(82), 8'(82') определяем аналогично, с помощью концентрической сферы, радиус которой принимается произвольно несколько большим по сравнению с радиусом вписанной сферы.

Полученные точки соединяем в плавную кривую линию: сначала соединяем точки 12®52=52'®72=72'®22, затем еще раз, стараясь, чтобы вторая кривая получилась симметрично первой, соединяем точки 32®62=62'®82=82'®42. Так как ось симметрии тора расположена || П1 и выше основания конуса, то плоскость этой оси для П1 будет являться плоскостью смены видимости. Линии пересечения, пройдя через эту плоскость, на П1 сменят видимость. Поэтому на оси симметрии необходимо отметить точки пересечения ее с линиями пересечения. Эти точки будут являться точками смены видимости (92=92' и 102=102')

Все полученные точки строятся на П1 по принадлежности конусу. Для построения их на П1 и соединяя их в линии, следует не забывать о смене видимости. Итак, левая линия - видимая часть 91®51®11®51'®91', невидимая - 91®71®21®71'®91'. Правая линия симметрична левой - видимая часть 101®61®31®61'®101' и невидимая часть 101®81®41®81'®101'. При решении задач способом концентрических сфер следует не забывать, что существуют особые случаи пересечения тел вращения (три теоремы).

6 Рекомендации по построению разверток

В задачах №3 и №4 одна из поверхностей помечена звездочкой. Это означает, что каждое из тел, отмеченных звездочкой в таблицах 3 и 4, необходимо построить развертку боковой поверхности с учетом полученной линии пересечения.

На образцах (рисунках 6 и 7) показано, как выполняются развертки. Допускается также построить обе развертки на формате А3, а задачи 3 и 4 также выполнить вместе без разверток.

Во всех вариантах в таблицах 3 и 4 заданы четыре типа разверток:

1. Призма, занимающая проецирующее положение.

2. Пирамида

3. Цилиндр - так же, как и призма, проецирующий

4. Конус

Рассмотрим на примере построение каждой из четырех возможных поверхностей.

Призма (рисунок 8); если она занимает проецирующее положение, то на одной из проекций - есть натуральная величина основания, а на другой проекции натуральная величина длины ребер.

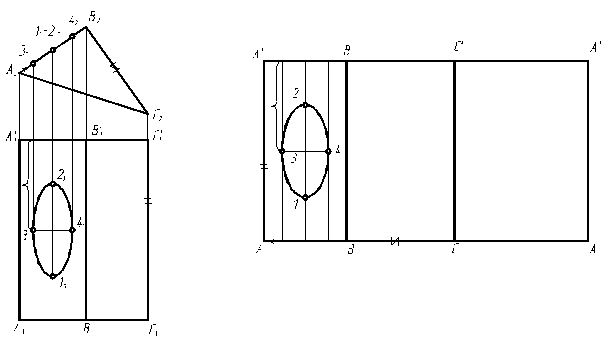
Рисунок 8 – Пример выполнения развертки призмы

Развертка такой призмы представляет собой прямоугольник, одна сторона которого равна длине ребер, другая - сумме сторон основания. При переносе линии пересечения можно воспользоваться уже найденными при построении точками. Сначала замеряется расстояние между точками на основании и переносится без искажений на сторону развертки, которая соответствует сумме сторон основания. Затем на другой проекции (там, где есть натуральная величина длины ребер) замеряется расстояние от точки до основания (на этой проекции основание должно проецироваться в прямую линию) и откладывается по другой стороне развертки, потом при помощи линий связи находим искомую точку. Когда все точки найдены, они соединяются в линию.

Пирамида (рисунок 9); так как боковые грани пирамиды являются треугольниками, то для построения развертки нужно построить натуральные виды этих треугольников. Для этого должны быть определены истинные величины всех ребер пирамиды.

Натуру ребер строим методом прямоугольного треугольника. Один катет треугольника равен высоте пирамиды, второй катет равен проекции ребра на П1, гипотенуза - натуральная величина ребра. Строим диаграмму натуральных величин ребер. Для удобства построения один катет прямоугольного треугольника, высота пирамиды (для всех ребер одинаковая) откладывается в проекционной связи с высотой пирамиды на П2. Аналогично находится любая точка на поверхности пирамиды.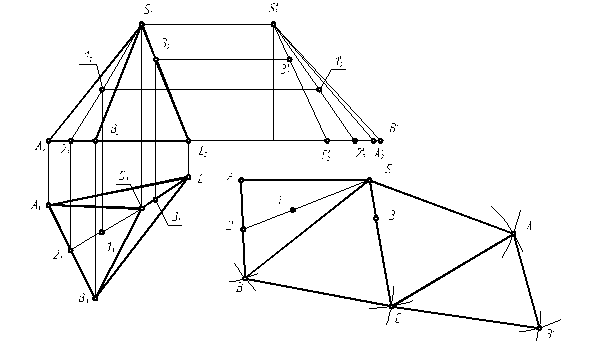

Рисунок 9 – Пример выполнения развертки пирамиды

Найдя натуру ребер, несложно построить развертку. Необходимо построить несколько треугольников, величина сторон которых заранее известна. Две стороны - это два ребра пирамиды, а оставшаяся сторона равна одной из сторон основания (основание пирамиды проецируется на П1 без искажений)

Цилиндр (рисунок 6). Эта развертка строится аналогично построению призмы. Так же, как и призма, цилиндр разворачивается в виде прямоугольника, одна из сторон которого равна высоте цилиндра, другая - длине окружности основания. Для удобства построения линии пересечения на развертке цилиндра кривую поверхность цилиндра приближенно заменяем поверхностями вписанных многогранников (т.е. вписанных призмой). При этом построение развертки можно выполнить с любой степенью точности за счет увеличения числа граней призмы. Сторона развертки, которая равна длине окружности, заменяется суммой хорд окружности.

Конус (рисунок 7), Развертка конуса выглядит в виде сектора круга. Радиус этого сектора равен длине образующей линии. Угол сектора считается по формуле φ=πD/l. Так же, как при построении развертке конуса, можно прибегнуть к способу приближения, т.е. окружность основания разбить на несколько частей и замерять хорды этих частей. При построении точек на поверхности следует помнить, что радиус замеряется только на очерковой образующей. Когда все точки найдены на развертке, они соединяются в плавную кривую линию.