Построение линии пересечения второго порядка (частные случаи)

В некоторых случаях кривая, которая получается при пересечении поверхностей вращения, распадается на две плоские кривые, т.е. на кривые второго порядка. Условия, при которых происходит распадение линии пересечения на две плоские кривые, оговариваются в трех теоремах:

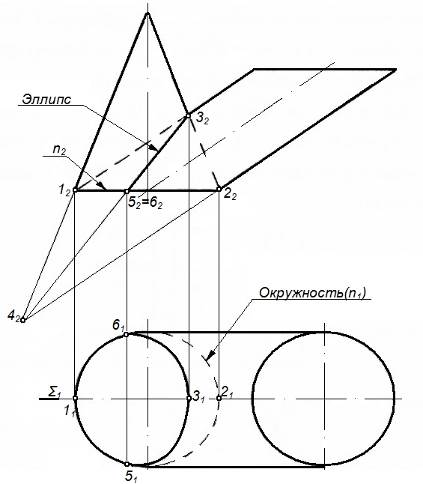
Рисунок 76 – Теорема 1

Теорема 1. Если две поверхности вращения (второго порядка) пересекаются по одной плоской кривой, то они пересекаются и еще по одной плоской кривой (рисунок 76).

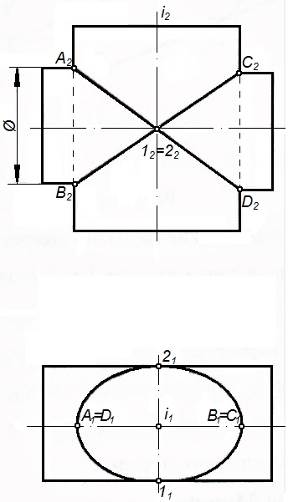
Рисунок 77 – Теорема 2

Теорема 2. Если две поверхности второго порядка имеют касание в двух точках, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания (рисунок 77).

На рисунке показано пересечение двух цилиндров второго порядка. Эти поверхности имеют две общие точки касания 1 и 2. Поэтому по теореме 2 они пересекаются по двум кривым второго порядка.

Теорема 3 (Теорема Монжа). Если две поверхности второго порядка описаны вокруг сферы (или вписаны в нее), то линия их пересечения распадается на две плоские кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания (рисунок 78).

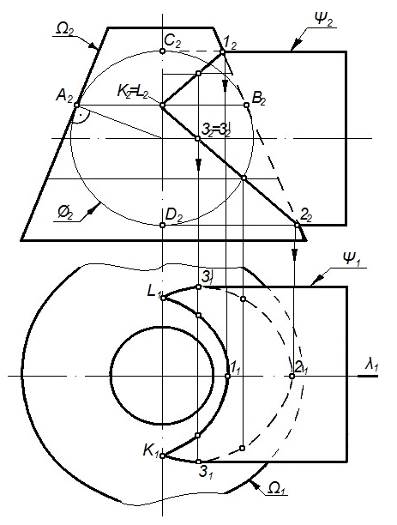
Рисунок 78 – Теорема 3

На рисунке 78 заданы две поверхности вращения (конус и цилиндр), описанные вокруг сферы Æ.

1. На основании теоремы Монжа искомая линия пересечения распалась на две плоские кривые второго порядка, плоскости которых проходят через прямую KL, соединяющую точки пересечения линий (a) касания сферы Æ и конуса W и (b) – касания сферы Æ и цилиндра y.

2. Опорные точки: 1 и 2 – экстремальные (они же очерковые относительно П2); 3 и 3¢ – очерковые относительно П1 (они же точки смены видимости на П1)

3. Промежуточные точки найдены из условия принадлежности.

4. Найденные точки соединены плавной кривой с учетом видимости.