Пересечение поверхности вращения проецирующей плоскостью

Линия пересечения поверхности вращения проецирующей плоскостью представляет собой плоскую замкнутую кривую. Для построения этой кривой определяем точки пересечения ряда образующих поверхности с секущей плоскостью. Среди точек пересечения имеются такие, которые особенно расположены по отношению к плоскостям проекций или занимают особые места на кривой. Такие точки называются опорными, и при построении сечения эти точки в первую очередь определяются и строятся. К опорным точкам относятся: экстремальные (высшая и низшая, ближняя и дальняя, левая и правая) и очерковые. В рассматриваемых задачах очерковые точки являются и точками смены видимости.

После определения опорных точек, для того чтобы точнее определить характер линии, определяется ряд случайных точек. Случайные точки – это точки, которые взяты произвольно. Чем больше найдено таких точек, тем точнее построено сечение.

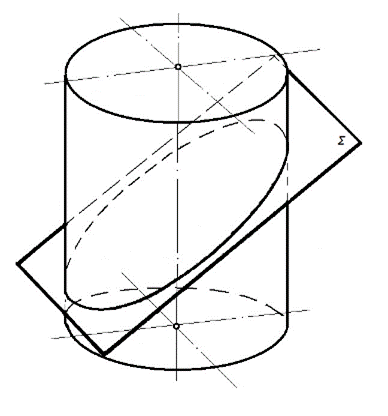
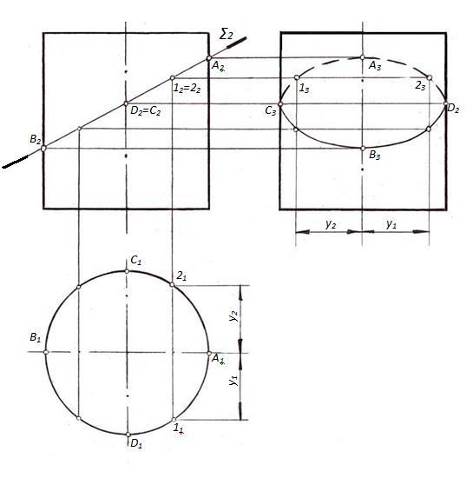
Рисунок 64 –Линия пересечения цилиндра с проецирующей плоскостью

Задача: Построить проекции линии пересечения цилиндра фронтально-проецирующей плоскостью.

На рисунке 64 секущая плоскость не перпендикулярна оси цилиндра. Линия сечения – эллипс.

На П2 эллипс проецируется в отрезок А2В2, на П1 – в окружность, совпадающую с горизонтальной проекцией цилиндра; на П3 – в эллипс. Точка А – высшая; В – низшая. Точки С и D очерковые относительно П3. Также точки С и D являются точками смены видимости на П3. Точки 1 и 2 – произвольные.

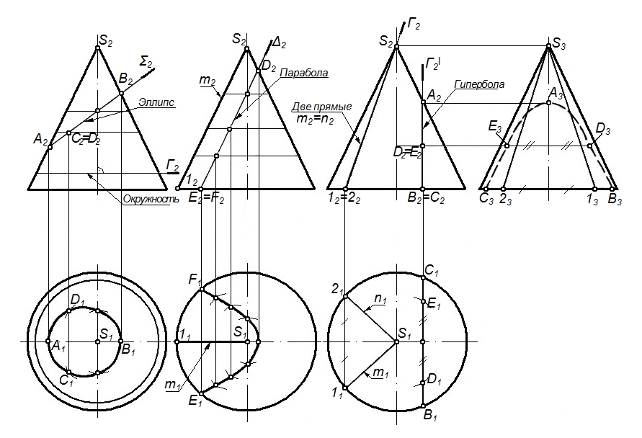
Рисунок 65 – Типы сечений конической поверхности

Конус – поверхность, в которой получается пять видов различных сечений:

- секущая плоскость (Г) проходит через вершину конуса, в сечении получается треугольник (все линии прямые);

- секущая плоскость (S) расположена под непрямым углом к основанию и не параллельна ни одной из образующих, в сечении получается эллипс;

- секущая плоскость (D) параллельна какой-либо одной образующей конуса, в сечении получается парабола;

- секущая плоскость (Г¢) параллельна оси вращения конуса, в сечении получается гипербола;

- секущая плоскость (Г₂) параллельна основанию и в прямом конусе перпендикулярна оси, в сечении получается окружность, радиус её измеряется от оси до очерка (рисунок 65).

В сечение сферической поверхности (рисунок 66) любой плоскостью всегда получается окружность.

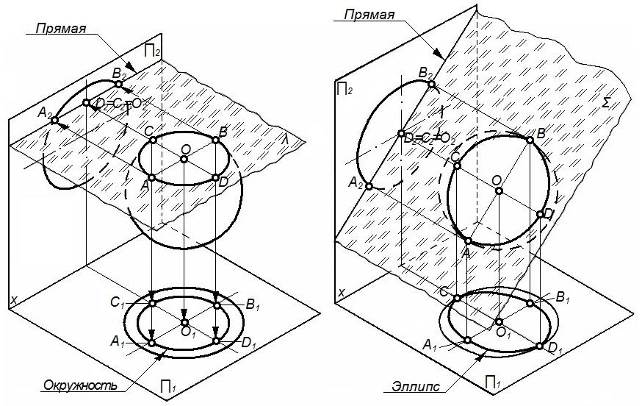
а) б)

Рисунок 66 – Сечение сферической поверхности

Проекции сечение могут изображаться: а) отрезком прямой и окружностью при сечении сферы плоскостями уровня (рис.66а); эллипсом и прямой сечении проецирующими плоскостями (рис.66б).

На рисунке 67 выполнено построение проекций сечения сферы горизонтальной плоскостью l.

На рисунке 68 выполнено построение проекций сечения сферы фронтально проецирующей плоскостью S.

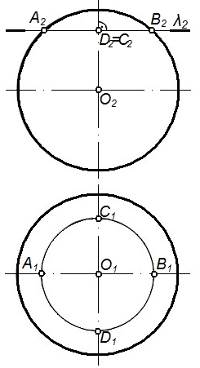
Рисунок 67-Построение сечения горизонтальной плоскостью l.

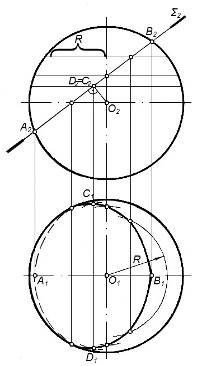
Рисунок 68-Построение сечения фронтально проецирующей плоскостью S.