Построение линии пересечения поверхностей методом вспомогательных концентрических сфер

Известно, что если ось поверхности вращения проходит через центр сферы и сфера пересекает эту поверхность, то линия пересечения – окружность, плоскость которой перпендикулярна оси поверхности вращения. При этом если ось поверхности вращения параллельна плоскости проекций, то линия пересечения на эту плоскость проецируется в отрезок прямой линии.

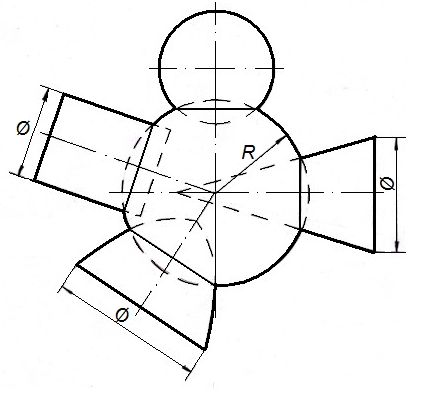
Рисунок 73 – Пересечение сферы с поверхностями вращения

На рисунке 73 показана фронтальная проекция линий пересечения сферой радиуса R с поверхностями вращения – конусом, тором, цилиндром, сферой, оси которых проходят через центр сферы. Окружности, по которым пересекаются указанные поверхности вращения с поверхностью сферы, проецируется на плоскость в виде отрезков прямых. Это свойство используется для построения линии пересечения двух поверхностей вращения с помощью вспомогательных сфер, но при следующих условиях:

1. Обе поверхности – поверхности вращения

2. Оси поверхностей пересекаются в точке (центр вспомогательных сфер)

3. Плоскость, образованная осями поверхностей (плоскость симметрии) должна быть параллельна плоскости проекции.

Задача. Построить проекции линии пересечения поверхностей цилиндра (Г) и конуса (y) (рисунок 74).

1. Заданы две поверхности вращения. Оси поверхностей пересекаются. Имеется общая плоскость симметрии l, параллельная П2.

2. Линия пересечения – пространственная замкнутая кривая 1-4-3-5-2-5¢-3¢-4¢-1 (рисунок 74).

3. Опорные точки: 1, 2 – экстремальные; точки 3 и 3¢ – очерковые относительно П1.

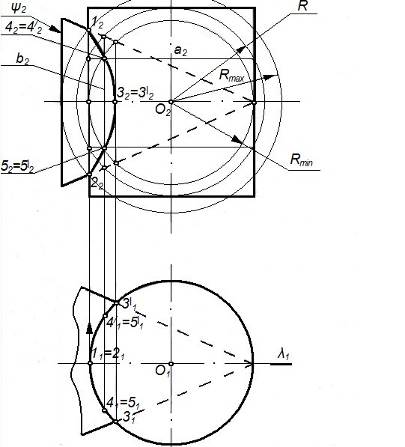
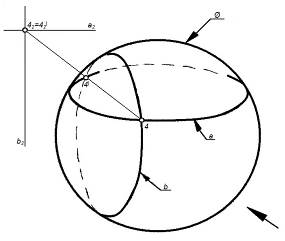
Рисунок 74 – Пересечение цилиндра и конуса

4. Промежуточные точки: 4, 4¢,5, 5¢ найдены с помощью вспомогательной сферы (Æ) с центром в точке О, соосной с заданными поверхностями.

5. Найденные точки соединены плавной кривой с учетом видимости.