Поверхности. Элементарные задачи на поверхности

Поверхностью называется совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону.

Линия, которая перемещаясь образует поверхность, называется образующей.

Линии, которые остаются неподвижными и с которыми при своем движении пересекается образующая, называются направляющими.

Сочетание образующих и направляющих называется каркасом поверхности.

Если образующая – прямая линия, то поверхность, образованная при помощи этой прямой линии, называется линейчатой.

Поверхность, которая образуется при помощи кривой линии, называется криволинейной. Условие, которое определяет поверхность, как совокупность всех положений образующей или направляющей, называется кинематическим законом образования поверхности.

Совокупность геометрических элементов, дающих возможность реализовать кинематический закон образования поверхности, называется определителем поверхности.

В число условий, входящих в состав определителя, должны быть включены:

а) геометрические фигуры, участвующие в образовании поверхности;

б) алгоритмическая часть или закон, указывающая на взаимосвязь между этими фигурами.

В общем случае определитель поверхности будет иметь следующую структурную формулу:

Ф(Г); [А], где

Ф – поверхность;

(Г) – геометрические элементы;

[А] – закон образования поверхности, указывающий на взаимосвязь между геометрическими элементами.

Задание поверхности определителем является позиционно полным и метрически определенным, т.е. на чертеже определителя поверхности можно решать любые позиционные и метрические задачи, связанные с самой поверхностью.

Чтобы задать поверхность на комплексном чертеже, необходимо задать ее проекциями определителя.

Например, для изображения на комплексном чертеже конической поверхности (рисунок 34) достаточно задать проекции вершины (точка) S(S1,S2), направляющей кривой m(m₁,m₂). И знать закон, указывающий на взаимосвязь между геометрическими элементами.

Задание конической поверхности (рисунок 34) является позиционно полным и метрически определенным, т.к. можно построить любое количество точек для решения соответствующих задач.

Ф(Г); [А], где

Ф – коническая поверхность

(Г): S (точка), m – направляющая

[А]: l Ì S; l ∩ m

Если в качестве направляющей будет взята ломаная линия, то коническая поверхность превратится в пирамидальную, а цилиндрическая – в призматическую.

Чертежи поверхностей заданных определителем обладают рядом достоинств (лаконичность, конкретность, простота), но имеют один недостаток – они не являются наглядными, т.к. не всегда просто представить форму заданных поверхностей. Поэтому поверхности на комплексном чертеже задают проекциями очерков (крайние очертания поверхности). Чертежи таких поверхностей называют основными.

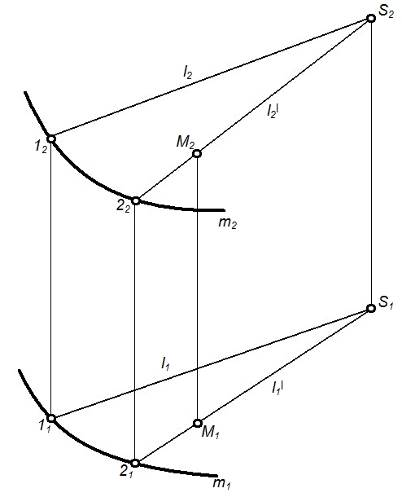
Рисунок 34 – Коническая поверхность

Прежде чем решать позиционные и метрические задачи, необходимо уметь решать элементарные задачи, т.е. задачи на принадлежность: линия принадлежит поверхности, если все точки линии принадлежат поверхности; точка принадлежит поверхности, если она принадлежит линии, принадлежащей поверхности.

Многогранники

Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником (рисунок 35).

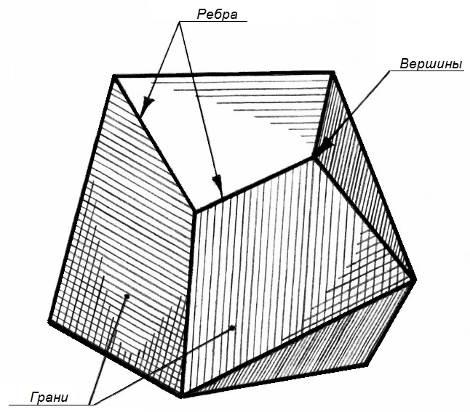
Рисунок 35 – Многогранник

Многогранники различают в зависимости от формы и количества граней.

Рассмотрим некоторые из многогранников, которые наиболее часто встречаются в технических чертежах.

Призма

Призма – многогранник, у которого две грани (основания) n-угольники, расположенные в параллельных плоскостях, а остальные n граней (боковые грани) – параллелограммы. Призма может быть прямой, если боковые ребра перпендикулярны основанию (рисунок 36) и наклонной, если ребра не перпендикулярны основанию. Прямая призма называется правильной, если в основании у нее правильный многогранник.

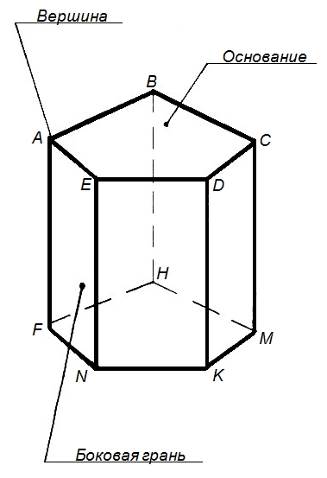
Рисунок 36 - Призма

Пирамида

Пирамида – многогранник, у которого боковые грани представляют собой треугольники, имеющие общую вершину. В основании у пирамиды – многоугольник. В зависимости от количества сторон основания пирамида называется трех-, четырех-, пятиугольной (рисунок 37) и т.д.

При изображениях на комплексных чертежах многогранников принято считать, что их грани непрозрачные и поэтому проекции отдельных ребер и граней будут невидимы. При решении вопросов видимости принимается следующие правила (рисунок 38):

1. Линии, образующие внешний контур (очерк) каждой проекции, всегда видимы.

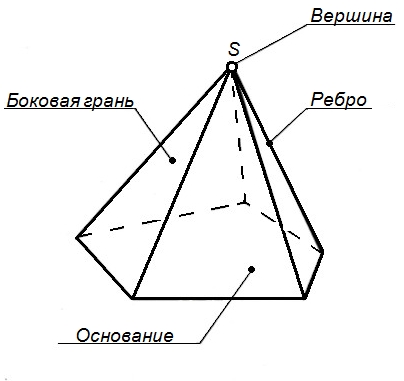
Рисунок 37 - Пирамида

2. Если внутри очерка пересекаются проекции двух ребер, то одна из них видимая, а другая невидимая (рисунок 38). Видимость определяется с помощью конкурирующих точек.

3. Если проекция хотя бы одного из ребер, ограничивающих грань, невидимая, то и вся грань невидимая.

4. На видимой грани лежат видимые элементы, на невидимой – невидимые.

5. Если в одной точке сходятся три или более ребер, то они все видимы или все невидимы.

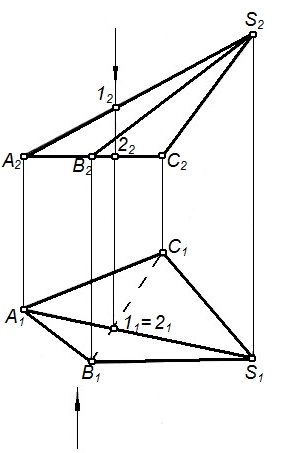
Рисунок 38 – Определение видимости пирамиды