Основные задачи преобразования

Таблица 3 – Основные задачи преобразования комплексного чертежа

Способ плоско-параллельного перемещения
Номер задачи	Комплексный чертеж	Схема решения	Область применения
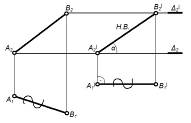
Первая – перевод прямой общего положения в линию уровня		Располагаем AB║П2, тогда располагаем А1B1' ^ вертикальным лин. связи; A1'B1'= A1B1, т.к. угол α-const.	Определение натуральной величины отрезка прямой линии и углов ее наклона к плоскостям проекций
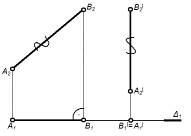
Вторая – перевод линии уровня в проецирующую прямую.		Располагаем AB║П1, тогда назначаем A2'B2'║ в.л. связи. B1'= A1' – точка.	1. Определение натуральных величин расстояний. 2. Определение натуры двугранного угла.
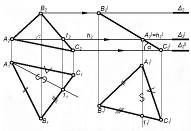
Третья – перевод плоскости общего положения проецирующую плоскость.		Располагаем ∆ABC^П2; тогда h^П2; Назначаем h1'║ в.л. связи. ∆A1'B1'C1'=∆A1B1C1 т.к. угол α-const. B2'A2'C2' – прямая.	1. Определение натуральной величины углов наклона плоскости к плоскости проекции. 2. Упрощение решения позиционных задач.
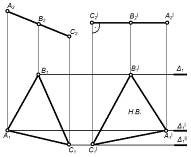
Четвертая – перевод проецирующей плоскости в плоскость уровня.		Располагаем ∆ABC║П1; назначаем C2'B2'A2' ^ в.л. связи; ∆ C2'A2'B2'=∆ABC – натура плоскости.	Определение натурального вида плоской фигуры, выполнение различных геометрических построений в плоскости фигуры

Способ замены плоскостей проекций
Номер задачи	Комплексный чертеж	Схема решения	Области применения
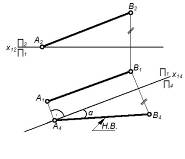
Первая – перевод прямой общего положения в линию уровня		Заменяем П2 на П1; располагаем П4║AB и П4^П1; тогда X14║A1B1; A4B4 – натура отрезка.	Определение натуральной величины отрезка прямой линии и углов ее наклона к плоскостям проекций
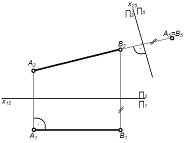
Вторая – перевод линии уровня в проецирующую прямую.		Заменяем П1 на П5; П5^AB; П5^П2, тогда X25^A2B2. B5= A5 – точка.	1. Определение натуральных величин расстояний. 2. Определение натуры двугранного угла.
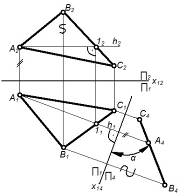
Третья – перевод плоскости общего положения в проецирующую плоскость.		Заменяем П2 на П4; располагаем П4^∆ABC, тогда П4^h – горизонталь плоскости. Располагаем X14^h, A4 B4C4 – прямая, т.е. проецир. пл-ть.	1. Определение натуральной величины углов наклона плоскости к плоскости проекции. 2. Упрощение решения позиционных задач.
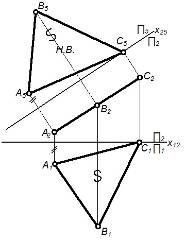
Четвертая – перевод проецирующей плоскости в плоскость уровня.		Заменяем П1 на П5; располагаем П5║∆ABC, тогда X25║A2B2C2; ∆A5B5C5=∆ABC – натура плоскости.	Определение натурального вида плоской фигуры, выполнение различных геометрических построений в плоскости фигуры

Изучив и запомнив основы способов плоско-параллельного перемещения и замены плоскостей проекций, следует научиться решать четыре основные задачи преобразования комплексного чертежа (таблица 3). Только после этого можно приступить к решению любых метрических задач.

Метрические задачи делятся на три основных группы:

1 группа – задачи на определение расстояния между геометрическими фигурами.

2 группа – задачи на определение действительных величин плоских фигур и углов.

3 группа – задачи связанные с построением в плоскости общего положения геометрических фигур по заданным размерам.

Приведем примеры.

Задача №1 (1 группа) определить расстояние между скрещивающимися прямыми АВ и СD (рисунок 30).

Расстояние между скрещивающимися прямыми выражается длиной перпендикуляра АВ и СD (рисунок 30а). Для определения его длины удобно, чтобы одна из прямых (например, АВ) располагалась перпендикулярно плоскости проекций. Для этого надо последовательно ввести две плоскости проекций (рисунок 30б).

Алгоритм решения:

1. P4‖АВ; P4 ^ P1; ось X14 ‖А1В1.

2. P5 ^ АВ; P5^ P4; ось X45 ^ А4В4.

3. АВ проецируется на P5 в точку (А5 = В5).

4. Опускаем перпендикуляр из точки А5 = В5 на С5D5 и находим N5.

5. Отметим M₅; N₅M₅ – искомое расстояние.

Строим проекции M1N1 и M2N2

а)
б)

Рисунок 30 – Пример решения метрической задачи №1

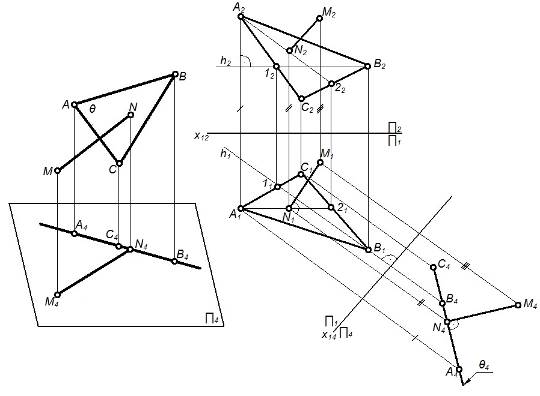
Задача №2(1 группа) Определить расстояние от точки М до плоскости общего положения θ(А₁В₁С₁, А₂В₂С₂) (рисунок 31).

Если проецировать плоскость θ(А₁В₁С₁, А₂В₂С₂) на плоскость П₄, перпендикулярную к θ, то эта плоскость проецируется в прямую θ₄ (рисунок 31а). Перпендикуляр MN, опущенный из точки М на плоскость θ, будет линией уровня по отношению к П₄. Поэтому перпендикуляр MN проецируется на П₄ без искажения, то есть MN = M₄N₄, причем M₄N₄ перпендикулярна θ₄. Таким образом плоскость θ надо сделать проецирующей.

Алгоритм решения:

1. Заменяем П₂ на П₄, тогда θ стала проецирующей (рисунок 31б) то есть на П₄ плоскость θ – прямая.

2. Опускаем из М перпендикуляр на θ₄.

3. M₄N₄ – искомое расстояние, причем его натуральная величина.

4. Обратным преобразованием построены проекции М₁N₁ и M₂N₂ отрезка MN.

а) б)

Рисунок 31 – Пример решения метрической задачи №2

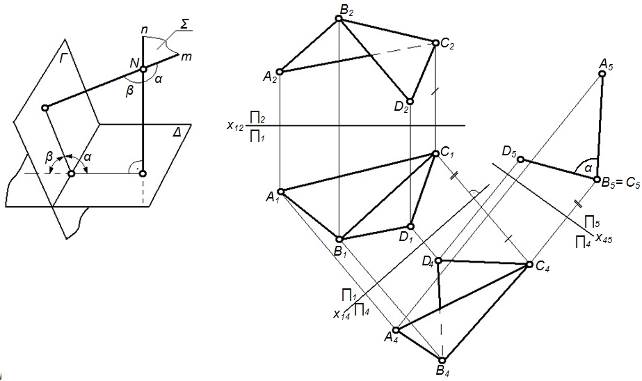
Задача №3 (2 группа) Определить величину угла между двумя плоскостями (рисунок 32).

а) б)

Рисунок 32 – Пример решения метрической задачи №3

Угол между плоскостями Г и ∆ (рисунок 32а) измеряется одним из его линейных углов, обычно острым, полученным при пересечении этих плоскостей третьей, перпендикулярной к ним.

Если линия пересечения плоскостей Г и ∆ (ребро двугранного угла) не задана, то определения искомого угла требует ряда дополнительных построений. Но их можно избежать, определяя угол b, заключенный между перпендикулярами m и n. Угол b является искомым если он острый; если же b - тупой, то искомый угол a = 180 - b.

Алгоритм решения следующий:

1. Из точки N провести m ^ Г и n ^∆.

2. Преобразовать плоскость ∑ (m Ç n) в плоскость уровня.

На рисунке 32б, показано определение двугранного угла, образованного плоскостями Г (АВС) и ∆ (ВСD), когда ребро ВС искомого угла задано. Задача решена преобразованием ВС в проецирующую прямую.

Задача №4 (3 группа) В плоскости q (a Ç b) построить равносторонний треугольник АВС, если радиус описанной окружности равен R (рисунок 33).

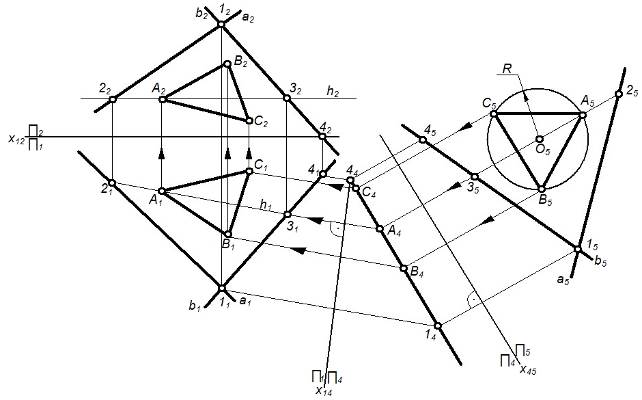
Рисунок 33 – Пример решения метрической задачи №4

Алгоритм решения:

1. преобразуем плоскость q (a Ç b) в плоскость уровня:

а) проводим в плоскости q горизонталь h (h1, h2);

б) проводим X14 ^h₁, тогда q - проецирующая;

в) проводим X45 ‖q(a4, b4), тогда q - плоскость уровня.

2. Строим в плоскости уровня q равносторонний треугольник А5В5С5, зная радиус описанной окружности.

3. Обратным преобразованием построены проекции А1В1С1 и А2В2С2 треугольника АВС.