Поверхности, образуемые вращением прямой (линейчатые поверхности вращения)

Вращением прямой линии образуются:

1. Цилиндр вращения, если прямая l параллельна оси i (рисунок 47а);

2. Конус вращения, если прямая l пересекает ось i (рисунок 49а)

3. Однополостный гиперболоид вращения (рисунок 51)

Все рассмотренные линейчатые поверхности вращения являются поверхностями второго порядка.

Построение проекций точки, принадлежащей каждой из них можно выполнить при помощи параллели или прямолинейной образующей, проходящей через нее.

Цилиндр

а) 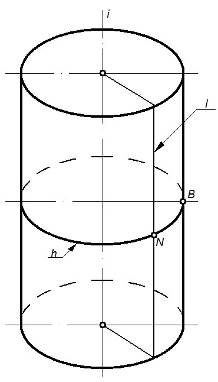б)

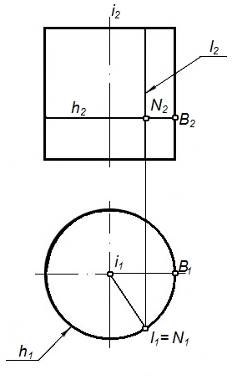
Рисунок 47 – Поверхность вращения - цилиндр

На рисунке 47а представлен цилиндр, который образован вращением прямой l параллельной оси вращения i. Ось вращения i расположена перпендикулярно П1 (рисунок 47б), следовательно, на П1 цилиндр проецируется в окружность, которая обладает собирательным свойством.

Задача. Построить недостающие проекции линии ABCD, принадлежащей поверхности цилиндра.

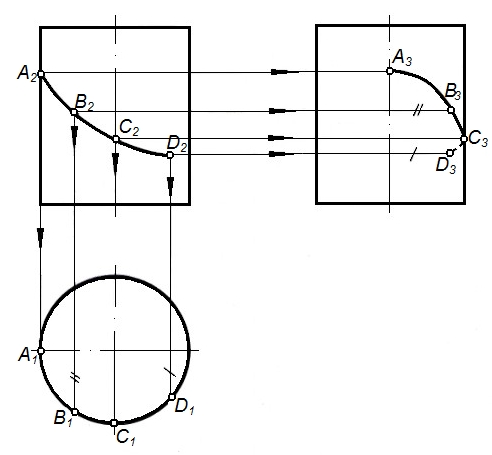
Рисунок 48 – Построение линии на поверхности цилиндра

На рисунке 48 задана фронтальная проекция линии (A2B2C2D2). Из условия принадлежности этой линии заданной поверхности построены ее недостающие проекции (A1B1C1D1 и A3B3C3D3).

Конус

На рисунке 49а изображен конус, который получен вращением прямой l вокруг оси i. Прямая пересекается с осью в точке S.

На рисунке 49б представлены проекции конуса и точки M (M1, M2), расположенной на его поверхности.

а) 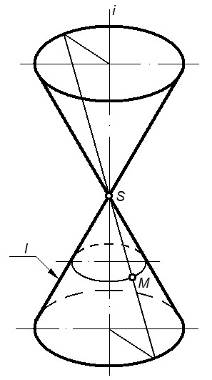б)

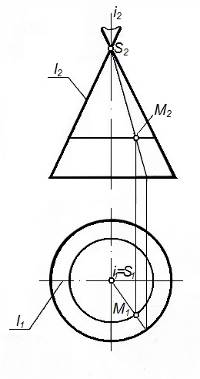
Рисунок 49 – Поверхность вращения - конус

Задача. Построить недостающие проекции точки С, линий АВ и DEFKG, если они принадлежат поверхности конуса.

На рисунке 50 показано нахождение точек и линий на поверхности конуса:

1. построение С2 и D2E2F2K2G2, если их горизонтальные проекции (С1 и D1E1F1K1G1) заданы.

2. Построение А1В1, если ее фронтальная проекция (А2В2) задана.

Недостающие проекции точек и линий построены из условия принадлежности их заданной поверхности.

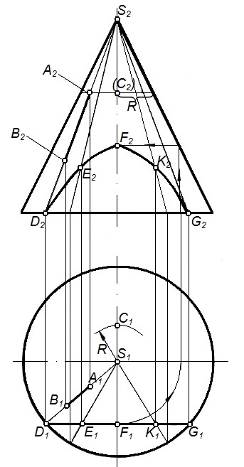
Рисунок 50 – Построение точек и линий на поверхности конуса