Статистическое имитационное моделирование в управлении запасами
Имитационное моделирование –процесс конструирования модели реальной системы и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить в рамках ограничений различные стратегии, обеспечивающие функционирование этой системы [3].
Статистическое имитационное моделирование –имитационное моделирование, при котором c помощью случайных чисел, формируемых ЭВМ, воспроизводятся случайные явления. В основе статистического имитационного моделирования лежит метод Монте-Карло.
Метод Монте-Карло - численный статистический метод, предполагающий использование специального аналитического аппарата (генератор случайных чисел в сочетании c интегральной функцией распределения вероятностей) и ЭВМ для получения данных о реализации во времени некоторого исследуемого процесса (например, расхода определенного товара на складе или выхода из строя оборудования). Данные по нескольким искусственно воспроизведенным реализациям случайного процесса используются в дальнейшем в качестве статистического материала, который может быть обработан обычными методами математической статистики.
Подавляющее большинство расчетов по методу Монте-Карло осуществляется c использованием псевдослучайных чисел. Под псевдослучайными числами понимают числа, получаемые с помощью специальных аналитических зависимостей и имитирующие значения случайной величины.
Статистическое имитационное моделирование в управлении запасами может быть использовано для решения следующих задач:
1. «Восстановить» процесс расхода (пополнения) запасов по неполным данным (средние значения, СКО и др.), то есть получить искусственным образом недостающие статистические данные, необходимые при прогнозировании.
2. Определить последствия применения различных стратегий управления запасами, а также сравнить эффективность различных систем управления запасами по результатам соответствующих имитационных экспериментов.
Рассмотрим порядок статистического имитационного моделирования процессов, связанных с пополнением (расходованием) запасов.
Прежде всего, необходимо определить параметры, подлежащие моделированию. К ним относят:
- расход запасов (λi);
- интервалы времени между заказами (Tj);
- сроки исполнения заказа (Lj);
Также могут моделироваться значения объемов поставки (Qпi) для того, чтобы учесть случаи не соблюдения поставщиком требований по объему, качеству, комплектности поставки.
Процесс статистического имитационного моделирования вышеназванных параметров может быть осуществлен следующим образом:
1. Задаются средние значения и средние квадратические отклонения значений моделируемых параметров (они могут быть определены заранее экспертным путем):
- среднее значение интенсивности потребления 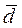 и СКО интенсивности потребления σd;
и СКО интенсивности потребления σd;
- средний интервал времени между заказами 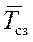 и СКОвремени между заказами σT;
и СКОвремени между заказами σT;
- среднее значение срока исполнения заказа 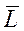 и СКО срока исполнения заказа σL.
и СКО срока исполнения заказа σL.
2. На основе средних значений и СКО для каждого параметра рассчитывается коэффициент вариации – υ по формуле:
 (9.21)
(9.21)

 где - среднее квадратическое отклонение моделируемого параметра «Х»;
где - среднее квадратическое отклонение моделируемого параметра «Х»;
- среднее значение моделируемого параметра.
3. По коэффициенту вариации определяется закон распределения, которому, как предполагается, подчинено распределение случайных значений моделируемых параметров процесса расхода (пополнения) запасов. В первом приближении выбор закона распределения может быть произведен по таблице 9.12.
Таблица 9.12
Законы распределения случайной положительной величины в зависимости от коэффициента вариации
| Пределы изменения коэффициента вариации | Закон распределения случайной величины |
| ν≤0,3 | Нормальный |
| 0,3 <ν <0,4 | Гамма-распределение |
| 0,4≤ ν <1 | Вэйбулла |
| ν=1 | Экспоненциальный |
4. С помощью генератора случайных чисел определяется массив случайных значений 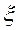 , которые затем будут использоваться для определения случайных значений моделируемых параметров. Для генерации случайных чисел может быть использован соответствующий инструмент Ms Excel.
, которые затем будут использоваться для определения случайных значений моделируемых параметров. Для генерации случайных чисел может быть использован соответствующий инструмент Ms Excel.
Количество генерируемых случайных чисел 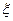 зависит от параметра, который необходимо получить в результате моделирования. Так для Тj (период времени между заказами) число случайных чисел
зависит от параметра, который необходимо получить в результате моделирования. Так для Тj (период времени между заказами) число случайных чисел 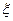 будет зависеть от количества сгенерированных случайных значений расхода запаса - Nd и от среднего значения периода времени между поставками (
будет зависеть от количества сгенерированных случайных значений расхода запаса - Nd и от среднего значения периода времени между поставками ( 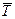 ):
):
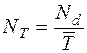 , (9.22)
, (9.22)
где NT - количество случайных чисел для Tj ;
Nd - количество сгенерированных случайных значений di;
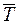 - среднее значение периода времени между заказами.
- среднее значение периода времени между заказами.
Количество значений Lj (время выполнения заказа), которое необходимо сгенерировать, соответствует числу NT. Например, генерируется 120 случайных величин расхода запаса, средний период времени между поставками 10 дней, следовательно, предполагаемое количество поставок равно 12.
5. Полученный после генерации вектор (столбец) случайных чисел 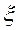 трансформируется, с учетом определенного ранее закона распределения, в случайные значения моделируемого параметра (di, Tj, Lj). Для этого используются специальные зависимости – см. табл. 9.13. Полученные по формулам значения округляются до целого (функция «округл» в Ms Excel).
трансформируется, с учетом определенного ранее закона распределения, в случайные значения моделируемого параметра (di, Tj, Lj). Для этого используются специальные зависимости – см. табл. 9.13. Полученные по формулам значения округляются до целого (функция «округл» в Ms Excel).
Таблица 9.13.
Формулы для моделирования случайных величин, подчиняющихся различным законам распределения
| Закон распределения случайной величины | Расчетная формула |
| Нормальный | 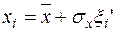
|
| Вэйбулла | 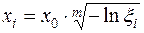
|
| Экспоненциальный | 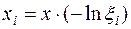
|
| Гамма-распределение | 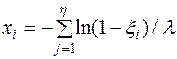
|
| Равномерный | 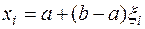
|
Примечание: 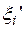 - нормально распределенная случайная величина со средним значением 0 и среднеквадратическим отклонением 1; - нормально распределенная случайная величина со средним значением 0 и среднеквадратическим отклонением 1; 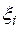 - равномерно распределенная случайная величина на интервале от 0 до 1. - равномерно распределенная случайная величина на интервале от 0 до 1.
|
Для распределения Вейбулла параметр положения x0 определяется по формуле:
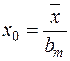 (9.23)
(9.23)
Коэффициент bm и параметр формы m можно определить по таблице 9.14.
Таблица 9.14
Коэффициенты для расчета параметров распределения
Вейбулла
| Коэффициент вариации | Коэффициент bm | Параметр m |
| 1,000 | 1,000 | 1,0 |
| 0,910 | 0,965 | 1,1 |
| 0,837 | 0,941 | 1,2 |
| 0,775 | 0,924 | 1,3 |
Окончание табл. 9.14
| Коэффициент вариации | Коэффициент bm | Параметр m |
| 0,723 | 0,911 | 1,4 |
| 0,681 | 0,903 | 1,5 |
| 0,640 | 0,897 | 1,6 |
| 0,605 | 0,892 | 1,7 |
| 0,575 | 0,889 | 1,8 |
| 0,547 | 0,887 | 1,9 |
| 0,523 | 0,887 | 2,0 |
| 0,499 | 0,886 | 2,1 |
| 0,480 | 0,886 | 2,2 |
| 0,461 | 0,886 | 2,3 |
| 0,444 | 0,886 | 2,4 |
| 0,428 | 0,887 | 2,5 |
Параметры гамма-распределения можно найти по формулам:
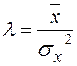 (9.24)
(9.24)
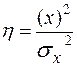 , (9.25)
, (9.25)
где 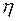 - целая часть числа от деления.
- целая часть числа от деления.
6. Определяется начальный уровень запаса на складе. Он может соответствовать реальным данным складской статистики, либо его можно рассчитать по формуле:
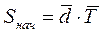 , (9.26)
, (9.26)
где 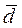 - среднее значение интенсивности потребления;
- среднее значение интенсивности потребления;
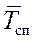 - средний интервал времени между поставками (время цикла).
- средний интервал времени между поставками (время цикла).
7. На основе полученного на предыдущих этапах массива исходных данных формируются временные ряды, отражающие процесс движения запасов на складе («приход», «расход», «остаток») под воздействием различных стратегий УЗ.
Таким образом, общий алгоритм статистического моделирования может быть представлен следующим образом:

Рис. 9.16. Блок-схема последовательности действий
при моделировании работы системы УЗ
Пример 9.5:
На основе описанного вышнее алгоритма осуществим статистическое моделирование процессов расхода и пополнения запаса.
1) Зададим исходные данные. Примем:
- среднее значение интенсивности потребления 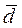 = 8 ед./день и СКО интенсивности потребления σD = 4,84 ед.;
= 8 ед./день и СКО интенсивности потребления σD = 4,84 ед.;
- средний интервал времени между заказами 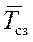 = 10 дней и СКОвремени между заказами σT = 2 дня;
= 10 дней и СКОвремени между заказами σT = 2 дня;
- среднее значение срока исполнения заказа 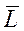 = 3 дня и СКО срока исполнения заказа σL = 1 день.
= 3 дня и СКО срока исполнения заказа σL = 1 день.
2) На основе средних значений и СКО для каждого параметра рассчитывается коэффициент вариации – υ:
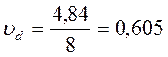 ;
; 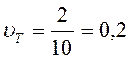 ;
; 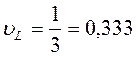
3) По коэффициентам вариации (табл. 9.12) определяем законы распределения случайных величин:
величине d в нашем примере соответствует закон распределения Вейбулла, величинам T и L – нормальный закон распределения.
4) Генерируем вспомогательные случайные величины для определения значений параметров d, T и L. Пусть спрос будет дан за 40 дней, тогда нам необходимо будет сгенерировать 40 случайных чисел ξ для определения d и 40/10 = 4 (см. форм. 9.22) случайных чисел для определения параметров T и L.
5) Произведем моделирование значений параметра d по формулам табл. 9.13 для закона распределения Вейбулла. По табл. 9.14 определяем значение параметров bm и m, соответствующих известному значению к-та вариации (ν=0,605). Так bm=0,892, m=1,7. Рассчитаем параметр x0: x0=8/0,892=8,97. Далее по формуле 9.27 определим объемы ежедневного расхода (их еще следует округлить до целого).
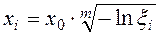 (9.27)
(9.27)
Например, при ξ = 0,973 находим:
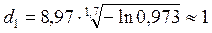
при ξ = 0,425:
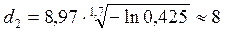
при ξ = 0,758:
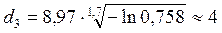
и т.д.
Результаты моделирования расхода представлены в табл. 9.15.
Таблица 9.15
Моделирование ежедневного расхода запаса (di)
| Номер дня | Случайная величина | Расход деталей di | Округленное значение расхода di |
| 0,973 | 1,065 | ||
| 0,425 | 8,170 | ||
| 0,758 | 4,208 | ||
| 0,185 | 12,190 |
Окончание табл. 9.15
| Номер дня | Случайная величина | Расход деталей di | Округленное значение расхода di |
| 0,649 | 5,470 | ||
| 0,465 | 7,656 | ||
| 0,563 | 6,468 | ||
| 0,617 | 5,838 | ||
| 0,955 | 1,447 | ||
| 0,311 | 9,826 | ||
| 0,017 | 20,482 | ||
| 0,438 | 8,010 | ||
| 0,498 | 7,249 | ||
| 0,024 | 19,374 | ||
| 0,793 | 3,794 | ||
| 0,540 | 6,735 | ||
| 0,352 | 9,195 | ||
| 0,610 | 5,914 | ||
| 0,685 | 5,058 | ||
| 0,623 | 5,774 | ||
| 0,690 | 5,002 | ||
| 0,259 | 10,686 | ||
| 0,501 | 7,209 | ||
| 0,629 | 5,702 | ||
| 0,074 | 15,702 | ||
| 0,592 | 6,124 | ||
| 0,950 | 1,546 | ||
| 0,213 | 11,578 | ||
| 0,699 | 4,897 | ||
| 0,065 | 16,164 | ||
| 0,057 | 16,634 | ||
| 0,624 | 5,760 | ||
| 0,356 | 9,138 | ||
| 0,188 | 12,116 | ||
| 0,130 | 13,640 | ||
| 0,919 | 2,083 | ||
| 0,415 | 8,309 | ||
| 0,714 | 4,728 | ||
| 0,820 | 3,461 | ||
| 0,920 | 2,078 |
6) Смоделируем значения T и L. Поскольку им соответствует один тип закона распределения (нормальный закон), подробный расчет можно показать лишь для одной величины, например, L.
Для расчетов воспользуемся формулой:
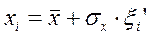 , (9.28)
, (9.28)
где 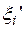 - нормально распределенная случайная величина со средним значением 0 и среднеквадратическим отклонением 1 (4 значения);
- нормально распределенная случайная величина со средним значением 0 и среднеквадратическим отклонением 1 (4 значения);
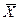 - среднее значение моделируемого параметра;
- среднее значение моделируемого параметра;
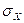 - СКО моделируемого параметра.
- СКО моделируемого параметра.
Произведем расчет для L:
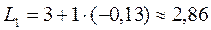
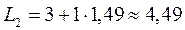
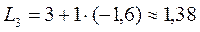
и т.д. (см. табл. 9.16.)
Результаты расчетов для Т приведены в табл. 9.17.
Таблица 9.16
Моделирование времени выполнения заказа (Lk)
| Случайная величина | Срок исполнения поставки Lk | Округленное значение Lk |
| -0,13393 | 2,866072 | |
| 1,492986 | 4,492986 | |
| -1,61832 | 1,381682 | |
| 0,232844 | 3,232844 |
Таблица 9.17
Моделирование интервалов времени между заказами (Tj)
| Случайная величина | Интервалы времени между поставками Tj | Округленное значение Tj |
| -0,7942 | 10,01448780 | |
| 0,517575 | 13,29393811 | |
| -0,03707 | 11,90731965 | |
| -0,43369 | 10,91576294 |
На базе полученных ранее значений ежедневных расходов запаса (di), интервалов времени между заказами (Tj) и сроков исполнения заказа (Lk) можно смоделировать процесс поступления и расхода запасов в условиях различных стратегий управления. Поскольку ранее нами уже были изучены основные стратегии управления запасами, в настоящем примере рассмотрим самый простой случай, не вдаваясь в оценку целесообразности его применения на практике.
Пусть стратегия управления запасами состоит в том, чтобы размещать одинаковые заказы (Qз = const) через равные промежутки времени (Tсз). Поставки будут осуществляться через время Lk после подачи клиентом соответствующего запроса. Будем считать, что величина поставки будет всегда соответствовать величине заказа (Qп = Qз).
В качестве исходных данных будем использовать:
- сгенерированные значения потребления (d) для периода в 40 дней (см. табл. 9.15);
- сгенерированные значения времени выполнения заказа (Lk) – см. табл. 9.16;
- в качестве постоянной периодичности заказов возьмем среднее время между заказами ( 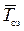 = 10 дней);
= 10 дней);
- для расчета Qз воспользуемся формулой:
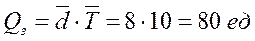
Результаты моделирования процессов расхода-пополнения запасов для данной стратегии приведены в табл. 9.18 и на рис. 9.17.
Таблица 9.18
Моделирование стратегии (T=cons, Q=const)
| День | спрос | заказ в конце дня | поставка в начале дня | остаток на начало дня | остаток на конец дня |
| 30-1=29 | |||||
| 80+17=97 | |||||
| 80+14=94 | |||||
| 80+33=113 | |||||
Окончание табл. 9.18
Моделирование стратегии (T=cons, Q=const)
| День | спрос | заказ в конце дня | поставка в начале дня | остаток на начало дня | остаток на конец дня |
| 80+9=89 | |||||
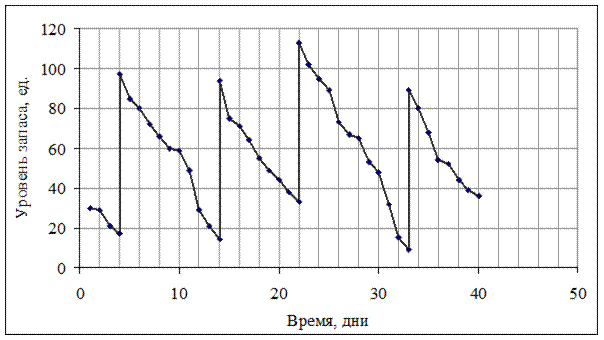
Рис. 9.17. Стратегия (T=cons, Q=const)
Вопросы и задания для самостоятельной работы
1. Что понимается под понятием «стратегия управления запасами»?
2. Охарактеризуйте структуру стратегий управления запасами.
3. Назовите основные типы стратегий управления запасами?
4. Перечислите основные параметры стратегий управления запасами.
5. Охарактеризуйте понятия: «редкий спрос», «импульсный спрос».
6. Чем «периодические стратегии» управления запасами отличаются от «стратегий с точкой заказа»?
7. Объясните принцип работы (R, Q) – стратегии.
8. В чем заключается сущность (S, s) – стратегии?
9. Какие стратегии управления запасами относят к комбинированным и почему? Объясните механизм работы данных стратегий.
10. Что такое статистическое имитационное моделирование?
11. В чем заключается сущность метода Монте-Карло?
12. Каков порядок (алгоритм) моделирования процессов, связанных с пополнением / расходованием запасов?
13. Для чего может использоваться статистическое имитационное моделирование в управлении запасами?
14. Какие параметры подлежат статистическому моделированию при управлении запасами?
15. Смоделируйте действие «стратегии оперативного управления» при следующих условиях:
- 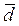 = 10 ед./сут, νd = 0,2;
= 10 ед./сут, νd = 0,2;
- Nd = 100 дней (число дней в рассматриваемом плановом периоде);
- Тсз – 30 дней;
- 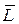 = 7 дней, σL= 1 день;
= 7 дней, σL= 1 день;
- начальный уровень запаса на складе = 50 ед.;
- неудовлетворенные заказы теряются;
- при расчете страхового запаса принимать вероятность отсутствия дефицита 94,5%;
- прогнозирование расхода за время поставки осуществлять методом экстраполяции тренда.
16. Смоделируйте действие «минимаксной стратегии» при условии, что:
- период инвентаризации (Δ) = 1 дню;
- 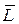 = 5 дней, σL= 1 день;
= 5 дней, σL= 1 день;
- 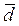 = 7 ед./сут, σd = 2 ед.;
= 7 ед./сут, σd = 2 ед.;
- Nd = 100 дней (число дней в рассматриваемом плановом периоде);
- начальный уровень запаса на складе = Smax;
- неудовлетворенные заказы теряются;
- при расчете страхового запаса принимать вероятность отсутствия дефицита 97,7%.
17. Назовите критерии, определяющие выбор стратегии управления запасами. Поясните механизм влияния этих критериев на выбор стратегии управления запасами.
18. Оптовый торговец автомобильными запасными частями продает двигатели к грузовым автомобилям КамАз. Спрос на двигатели составляет порядка 250 ед. в квартал. Затраты на размещение заказа у поставщиков составляют порядка 100000 руб. за одну партию. Стоимость одного двигателя – 215000 руб. Ежемесячные затраты на хранение одного двигателя составляют порядка 0,2% от его цены. Время поставки партии – две недели. Возможная задержка – одна неделя.
На основании изложенных выше данных рассчитайте параметры стратегии управления запасами с фиксированным размером заказа ((R,Q) -стратегия).
Примечание: при расчетах учтите, что спрос на двигатели постоянен и равномерно распределен во времени, а мониторинг уровня запаса на складе компании может осуществляться через складское ПО в режиме «реального времени».
Дата добавления: 2016-01-07; просмотров: 1374;
