Периодические стратегии управления запасами
Рассмотрим так называемую «стратегию оперативного управления» - рис. 9.6.

Smax – максимально желаемый размер запаса, ед.; Sт – текущий запас, ед.; Smi – уровень запаса на момент размещения заказа, ед.; Sс – страховой запас, ед.; Qз – размер заказа, ед.; d(L) – ожидаемый расход запаса за время поставки, ед.; d(L)факт – фактический расход запаса за время поставки, ед.; tз – момент размещения заказа на поставку; L – время выполнения заказа, дней; tп – момент осуществления поставки; T`- интервал времени между поставками, дней; Tсз – период времени между заказами (const), дней.
Рис. 9.6.Стратегия «оперативного управления»
В «стратегии оперативного управления» период между заказами постоянен (Tсз=const), заказы на пополнение запаса делаются в строго определенные моменты времени (tз). Объем заказа (Qз) переменный и рассчитывается таким образом, чтобы уровень запаса после поставки достиг «максимально желаемого уровня» (Smax). При определении объема заказа учитывается текущий уровень запаса на момент подачи заказа Sтi, ожидаемый расход запаса за время выполнения поставки d(L), запасы в пути (ЗП).
Если Tсз (период времени между заказами) больше L (время выполнения заказа), то заказ в «стратегии оперативного управления» производится между двумя смежными поставками. Это наиболее желательный вариант при формировании периодических стратегий управления запасами. Если Tсз меньше L, то это приводит к появлению за время L двух или более заказов. Другими словами, заказ производится в то время, когда предыдущий заказ не поступил потребителю. Это приводит к росту неопределенности системы управления запасами, особенно при больших вариациях ежедневного расхода и времени выполнения заказа.
Формулы для расчета параметров периодической стратегии «оперативного управления» приведены в табл. 9.2.
Таблица 9.2
Параметры стратегии «оперативного управления»
| № | Показатель | Порядок определения показателей | |
| Детерминированный вариант | Стохастический вариант | ||
| Интервал времени между заказами – Тсз, дней; Тсз = const. | - рассчитывается на основе модели EOQ:
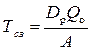 ,
где Qо – оптимальная партия поставки (модель Харриса-Уилсона);
Dр- число рабочих дней за рассматриваемый период.
А – общая потребность в продукте за рассматриваемый период (например, год); определяется на основе плана производства или реализации. ,
где Qо – оптимальная партия поставки (модель Харриса-Уилсона);
Dр- число рабочих дней за рассматриваемый период.
А – общая потребность в продукте за рассматриваемый период (например, год); определяется на основе плана производства или реализации.
| - соответствует установленному на предприятии периоду инвентаризации. | |
| Время выполнения поставки - L, дней | - обычно указывается в договоре на поставку; | - определяется статистически на основе данных по прошлым поставкам:
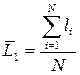 или или 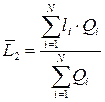 ,
где li – значение времени выполнения i-й поставки, дней;
Qi – величина i-й поставки, ед.; ,
где li – значение времени выполнения i-й поставки, дней;
Qi – величина i-й поставки, ед.;
|
Продолжение табл. 9.2
| № | Показатель | Порядок определения показателей | |
| Детерминированный вариант | Стохастический вариант | ||
| Возможное время задержки поставки – τ (σL), дней. | - определяется эмпирически как наибольшее время, на которое может быть задержана поставка) - τ; | - рассчитывается на основании данных о предыдущих поставках:
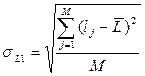 или или 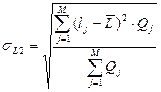
| |
| Интенсивность потребления– d, ед./день |
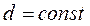 или
или
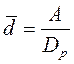
| - среднее значение:
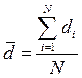 ,
где di – расход в i-й момент времени; N – объем выборки
- прогноз. ,
где di – расход в i-й момент времени; N – объем выборки
- прогноз.
| |
| СКО интенсивности потребления – σd | - среднее квадратическое отклонение (СКО): 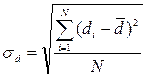
| ||
| Потребление за время поставки – d(L), ед. | 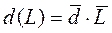 - среднее потребление - среднее потребление
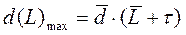 - максимальное потребление - максимальное потребление
| - метод экстраполяции тренда; - другие методы прогнозирования. |
Окончание табл. 9.2
| № | Показатель | Порядок определения показателей | |
| Детерминированный вариант | Стохастический вариант | ||
| Страховой запас - Sс, ед. |
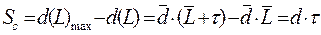
| 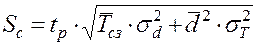 ,
где ,
где 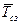 - среднее значение периода времени между заказами, дней - среднее значение периода времени между заказами, дней
| |
| Sт – текущий запас, ед. | 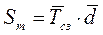
| 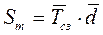
| |
| Максимально желаемый объем запаса– Smax , ед. | 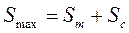
| 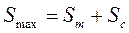
| |
| Размер заказа – Qз, ед. | 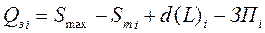 ,
где Qзi – размер заказа в момент времени i;
Sтi – уровень располагаемого запаса на момент времени i;
ЗПi – запас в пути на момент времени i. ,
где Qзi – размер заказа в момент времени i;
Sтi – уровень располагаемого запаса на момент времени i;
ЗПi – запас в пути на момент времени i.
| 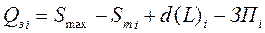 ,
где Qзi – размер заказа в момент времени i;
Sтi – уровень располагаемого запаса на момент времени i;
ЗПi – запас в пути на момент времени i. ,
где Qзi – размер заказа в момент времени i;
Sтi – уровень располагаемого запаса на момент времени i;
ЗПi – запас в пути на момент времени i.
|
Пример 9.1:
В качестве примера рассмотрим процесс реализации некоторого товара «Х» со следующими характеристиками:
- среднесуточный расход ( 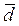 ) = 8 шт./день;
) = 8 шт./день;
- СКО среднесуточного расхода (σd) = 2,4 шт./день;
- коэффициент вариации среднесуточного расхода (νd) = 0,3;
- периодичность заказа (Тсз) = 12 дней;
- средний (ожидаемый) срок исполнения заказа ( 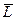 ) = 3 дня;
) = 3 дня;
- СКО срока исполнения заказа (σL) = 1
- коэффициент вариации срока исполнения заказа (νL) = 0,33.
Предположим также, что заказ на пополнение запасов подается в начале дня и поставки также осуществляется в начале дня.
В отсутствии реальных данных о фактических сроках исполнения заказов поставщиком (Li) допустим, что:
- срок выполнения поставщиком 1-ого заказа составляет L1=3 дня;
- 2-ого заказа L2= 4 дня;
- 3-его заказа L3= 1 день;
- 4-ого заказа L4= 3 дня;
- 5-ого заказа L5= 4 дня и т.д.
Ограничим рассматриваемый период реализации продукции 46-ю днями.
Рассмотрим, как отразится на уровне запасов применение стратегии «оперативного управления».
Учитывая периодичность заказов 12 дней (Тсз = const) и средний (ожидаемый) срок исполнения заказа 3 дня ( 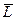 ), первый заказ будет подаваться на 9-й день (12-3=9); 2-й заказ - на 21-й день (12х2–3=21); 3-й заказ - на 33-й день (12х3–3=33) и т.д.
), первый заказ будет подаваться на 9-й день (12-3=9); 2-й заказ - на 21-й день (12х2–3=21); 3-й заказ - на 33-й день (12х3–3=33) и т.д.
Для расчета страхового запаса воспользуемся соответствующей формулой из табл. 9.2:
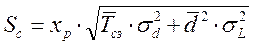 , (9.1)
, (9.1)
где в качестве коэффициента хp возьмем 2, что соответствует вероятности отсутствия дефицита продукции на складе Р= 98% (табл. 3.1).
Рассчитаем страховой запас:
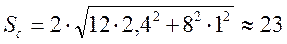
Поскольку стратегия «оперативного управления» предполагает пополнение запасов до максимального уровня (Smax), рассчитаем этот уровень, воспользовавшись формулами из табл. 9.2:
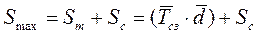 (9.2)
(9.2)
Получим 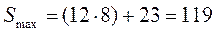 .
.
Примем, что на начало 1-ого дня рассматриваемого 46-ти дневного периода реализации товара «Х» на складе будет находиться его максимальный уровень, то есть 119 ед.
Расчет размеров заказов на пополнение запаса в системе будем осуществлять по формуле:
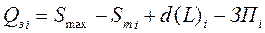 (9.3)
(9.3)
В расчетах примем, что:
- запасы в пути (ЗП) будут всегда равны 0;
- для прогноза расхода товара за время выполнения поставки ( 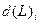 ) воспользуемся формулой:
) воспользуемся формулой:
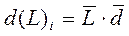 (9.4)
(9.4)
Величина заказа в первом цикле 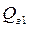 рассчитывается следующим образом: из максимального начального уровня запаса (Smax), равного 119 ед. вычитаем остаток запаса на момент размещения заказа (на 9-й день, см. табл. 9.3), равный 35 ед., прибавляем расчетную величину расхода запаса за ожидаемое время выполнения заказа (
рассчитывается следующим образом: из максимального начального уровня запаса (Smax), равного 119 ед. вычитаем остаток запаса на момент размещения заказа (на 9-й день, см. табл. 9.3), равный 35 ед., прибавляем расчетную величину расхода запаса за ожидаемое время выполнения заказа ( 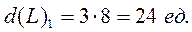 ), затем вычитаем величину «заказов в пути» (заказанных ранее, но еще не поступивших на склад), которые в нашем примере равны 0.
), затем вычитаем величину «заказов в пути» (заказанных ранее, но еще не поступивших на склад), которые в нашем примере равны 0.
В результате получим:
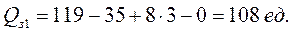
Таким образом, в конце 9-ого дня первого цикла размещается заказ в размере 108 ед. Фактический срок выполнения этого заказа L1=3 дня, следовательно, заказ будет выполняться 10-й, 11-й и 12-й день, и поступит на склад в начале 13-ого дня (см. табл. 9.3). Остаток на 12-й день составил 9 ед. Таким образом, фактический запас в начале второго цикла составляет 9 + 108 = 117 ед.
Следующий момент размещения заказа наступит на 21-й день. Остаток в конце 21-ого дня (на момент размещения 2-ого заказа) составляет 34 ед., следовательно:
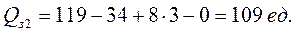
Срок выполнения 2-ого заказа L2=4 дня, следовательно, заказ будет выполняться 22-й, 23-й, 24-й, и 25-й день и поступит на склад в начале 26-ого дня (см. табл. 9.3). Остаток на 25-й день составит 0, а накопленный к этому моменту дефицит = 2 ед. Предположим, что дефицит будет компенсирован из поставки. Таким образом, фактический запас в начале третьего цикла (на начало 26-ого дня) составит (- 2) + 109 = 107 ед.
Аналогичным образом определяются величины заказов в последующих циклах:
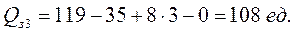 ;
;
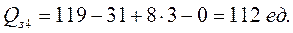
Результаты моделирования действия стратегии «оперативного управления» приведены в табл. 9.3. и на рис. 9.7.
Таблица 9.3
Результаты моделирования стратегии «оперативного управления»
| Номер дня | Спрос di | Запас на складе, ед. | Дефицит, ед. | Величина заказа | Величина поставки | ||
| на начало дня | на конец дня | на начало дня | на конец дня | ||||
Продолжение табл. 9.3
| Номер дня | Спрос di | Запас на складе, ед. | Дефицит, ед. | Величина заказа | Величина поставки | ||
| на начало дня | на конец дня | на начало дня | на конец дня | ||||
| -2 | |||||||
Окончание табл. 9.3
| Номер дня | Спрос di | Запас на складе, ед. | Дефицит, ед. | Величина заказа | Величина поставки | ||
| на начало дня | на конец дня | на начало дня | на конец дня | ||||
| И т.д. | … | … | … | … | …. | …. | … |
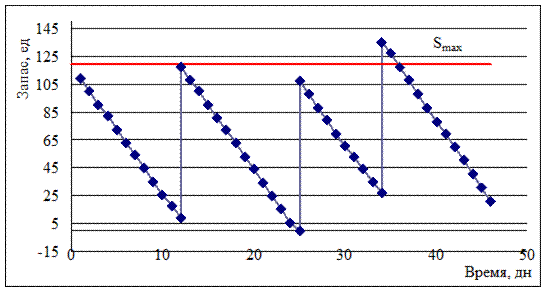
Рис. 9.7. Стратегия «оперативного управления»
Рассмотрим теперь периодическую стратегию«равномерной поставки»(с постоянным размером заказа)(рис. 9.8).
В классической трактовке стратегии «равномерной поставки» период между заказами постоянен(Tсз=const) и объем заказа также постоянен (Qopt=const). Предлагаем откорректировать классический подход, добавив к постоянной составляющей (Qopt=const) переменную величину (Sc(L)), которая идет на покрытие израсходованного в предыдущем периоде страхового запаса (Sc(L)). Восполнение страхового запаса может происходить как в период следующей поставки, так и в период между поставками. Формулы для расчета параметров стратегии приведены в табл. 9.4.
|

Sт – текущий запас, ед.; Sс – страховой запас, ед.; Sс(L)- частьстрахового запаса, израсходованная за время поставки (L)ед.; Qз – размер заказа, ед.; Qopt – постоянная, оптимальная, составляющая заказа на пополнение запаса; d(L)факт – фактический расход запаса за время поставки, ед.; tз – момент размещения заказа на поставку; L – время выполнения заказа, дней; tп – момент осуществления поставки; T`- интервал времени между поставками, дней; Tсз – период времени между заказами (const), дней.
Рис. 9.8.Стратегия «равномерной поставки» (с постоянным размером заказа)
Таблица 9.4
Параметры стратегии «равномерной поставки» (с постоянным размером заказа)
| № | Показатель | Порядок определения показателей |
| Sн – начальный уровень запаса | 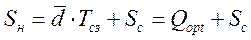 ,
где Тсз – интервал времени между заказами; Sс- страховой запас; Qopt – оптимальная составляющая размера заказа; ,
где Тсз – интервал времени между заказами; Sс- страховой запас; Qopt – оптимальная составляющая размера заказа; 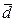 - среднесуточный расход. - среднесуточный расход.
| |
| Интервал времени между заказами – Тсз, дней; Тсз = const. | - рассчитывается на основе модели EOQ:
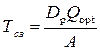 ,
где Qopt – оптимальная партия поставки (модель Харриса-Уилсона); Dр- число рабочих дней за рассматриваемый период. А – общая потребность в продукте за рассматриваемый период (например, год); определяется на основе плана производства или реализации. ,
где Qopt – оптимальная партия поставки (модель Харриса-Уилсона); Dр- число рабочих дней за рассматриваемый период. А – общая потребность в продукте за рассматриваемый период (например, год); определяется на основе плана производства или реализации.
| |
| Время выполнения поставки - L, дней | - обычно указывается в договоре на поставку; | |
| Возможное время задержки поставки – τ (σL), дней. | - определяется эмпирически как наибольшее время, на которое может быть задержана поставка) - τ; | |
| Интенсивность потребления– d, ед./день | 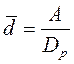
| |
| Страховой запас - Sс, ед. | вариант 1:
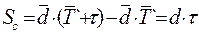 вариант 2:
вариант 2:
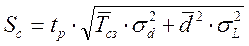 ,
где ,
где 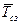 - среднее значение периода времени между смежными заказами, дней. - среднее значение периода времени между смежными заказами, дней.
|
Окончание табл. 9.4
| № | Показатель | Порядок определения показателей |
| Размер заказа – Qз, ед. | 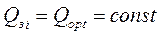 или или 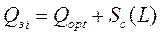 ,
где Qзi – размер заказа в момент времени i;
Qopt – оптимальная составляющая размера заказа, она постоянна; Sc (L)– часть страхового запаса, израсходованная за время поставки (L)ед. ,
где Qзi – размер заказа в момент времени i;
Qopt – оптимальная составляющая размера заказа, она постоянна; Sc (L)– часть страхового запаса, израсходованная за время поставки (L)ед.
| |
| Qopt оптимальная составляющая размера заказа, ед. | модель EOQ | |
| Sc (L) частьстрахового запаса, израсходованная за время поставки (L), ед. | - определяется по фактическим данным складского учета |
Пример 9.2:
Воспользуемся исходными данными из примера 9.1 о параметрах реализации товара «Х» и смоделируем действие стратегии «равномерной поставки» (с постоянным размером заказа) для периода в 46 дней.
Рассчитаем периодичность подачи заказов на пополнение запаса (Тсз):
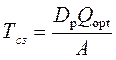 (9.5)
(9.5)
Для расчета нам потребуются данные об общей ожидаемой потребности в товаре «Х» за весь рассматриваемый период (A) и оптимальном объеме заказа (Qopt).
Примем, что число рабочих дней в рассматриваемом периоде 46 (Dр), затраты на осуществление заказа (С0) составят 1000 у.е., затраты на хранение единицы продукции (Схр) – 100 у.е. за рассматриваемый период 46 дней.
Рассчитаем оптимальный объем заказа (Qopt), воспользовавшись классической моделью EOQ Харриса-Уилсона:
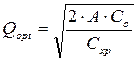 (9.6)
(9.6)
Для оценки значения плановой потребности за весь рассматриваемый период (A) воспользуемся формулой:
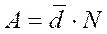 , (9.7)
, (9.7)
где N – общее число дней в рассматриваемом периоде (равно 46 в рассматриваемом примере);
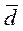 - среднесуточный расход товара «Х», который мы возьмем из исходных данных к примеру 9.1.
- среднесуточный расход товара «Х», который мы возьмем из исходных данных к примеру 9.1.
Получаем:
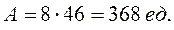
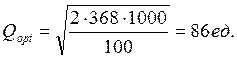
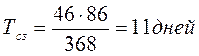
Исходя из полученной оптимальной периодичности размещения заказов Тсз = 11 дней (Тсз = const) и среднего (ожидаемого) срока исполнения заказа 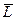 =3 дня, первый заказ будет подаваться на 8-й день (11-3=8); 2-й заказ - на 19-й день (11х2–3=19); 3-й заказ - на 30-й день (11х3–3=30) и т.д.
=3 дня, первый заказ будет подаваться на 8-й день (11-3=8); 2-й заказ - на 19-й день (11х2–3=19); 3-й заказ - на 30-й день (11х3–3=30) и т.д.
Реальный срок исполнения заказа Li обычно отличается от ожидаемого срока выполнения заказа 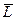 =3 дня. Примем в расчетах следующие сроки выполнения заказов для каждого цикла:
=3 дня. Примем в расчетах следующие сроки выполнения заказов для каждого цикла:
- срок выполнения поставщиком 1-ого заказа составляет L1=3 дня;
- 2-ого заказа L2= 4 дня;
- 3-его заказа L3= 1 день;
- 4-ого заказа L4= 3 дня;
- 5-ого заказа L5= 4 дня и т.д.
Первый цикл: размещение заказа на конец 8-го дня, исполнение заказа L1=3 дня (9-й, 10-й, 11-й день).
Второй цикл: начало цикла – 12-й день, размещение заказа на 19-й день, срок выполнения заказа L2= 4 дня (20-й, 21-й, 22-й, 23-й день).
Третий цикл: начало цикла – 24-й день, размещение заказа на 30-й день, срок выполнения заказа L3= 1 дня (31-й день) и т.д.
Для расчета страхового запаса воспользуемся формулой из табл. 9.4.
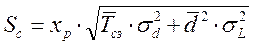 (9.8)
(9.8)
Коэффициент хp берем таким же как и в примере 9.1. Получим:
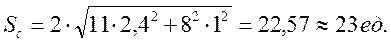
Начальный запас в системе рассчитаем по формуле:
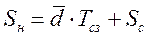 (9.9)
(9.9)
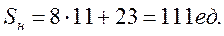
Результаты моделирования действия стратегии «равномерной поставки» приведены в табл. 9.5. и на рис. 9.9.
Таблица 9.5
Результаты моделирования стратегии «равномерной поставки»
| Номер дня | Спрос di | Запас на складе, ед. | Дефицит, ед. | Величина заказа | Величина поставки | ||
| на начало дня | на конец дня | на начало дня | на конец дня | ||||
Окончание табл. 9.5
| Номер дня | Спрос di | Запас на складе, ед. | Дефицит, ед. | Величина заказа | Величина поставки | ||
| на начало дня | на конец дня | на начало дня | на конец дня | ||||
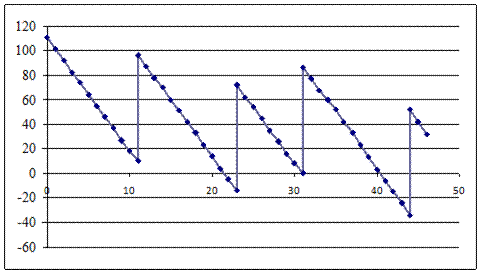
Рис. 9.9. Стратегия «равномерной поставки»
Следует отметить, что для расчета объемов заказов на пополнение запаса можно воспользоваться альтернативной формулой, в которой учитывается необходимость пополнения израсходованного страхового запаса:
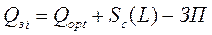 (9.10)
(9.10)
Например, на конец первого цикла (табл. 9.5) остаток составляет 10 единиц, следовательно, страховой запас израсходован в количестве 13 единиц (23 – 10 = 13), которые по формуле (9.10) включаются в следующий заказ. Таким образом, заказ во втором цикле составил бы 99 единиц.
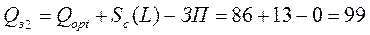 .
.
9.4. Стратегии управления с «точкой заказа»
Рассмотрим так называемую (R; Q)-стратегию или «стратегию с фиксированным размером заказа» (рис. 9.10).
В стратегии с фиксированным размером заказа заказ на пополнение запаса делается по достижении определенного порогового уровня текущего запаса или «точки заказа» (ROP). Объем заказа является постоянной величиной (Qз=Qopt=const). Стратегия предполагает непрерывный или периодический контроль уровня запаса (Δ→0 или Δ = const).
Формулы для расчета параметров (R; Q) - стратегии приведены в табл. 9.6.

Sт – текущий запас, ед.; Sс – страховой запас, ед.; Qз – размер заказа, ед.; Qopt – постоянная, оптимальная, составляющая заказа на пополнение запаса; tз – момент размещения заказа на поставку; L – время выполнения заказа, дней; tп – момент осуществления поставки; T`- интервал времени между поставками, дней; Δ – период контроля состояния запасов на складе, дней; ROP – точка заказа, ед.
Рис. 9.10. Стратегия с «точкой заказа» и фиксированным размером заказа, (R; Q) - стратегия
Таблица 9.6
Параметры (R; Q)-стратегии
| № | Показатель | Формула для расчета |
| Интервал между проверками уровня запаса – Δ | - определяется в соответствии с условиями работы склада компании и уровнем автоматизации; может быть непрерывным (в режиме on-line) в случае соответствующего информационного обеспечения склада (Δ→0); может быть периодическим, например, через день, или 1 раз в неделю (Δ = const). |
Продолжение табл. 9.6
| № | Показатель | Формула для расчета |
| Время выполнения поставки – L, дней | - обычно указывается в договоре на поставку (среднее значение);
- определяется статистически на основе данных по прошлым поставкам:
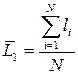 или или 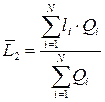 ,
где li – значение времени выполнения i-й поставки, дней; Qi – величина i-й поставки, ед.; ,
где li – значение времени выполнения i-й поставки, дней; Qi – величина i-й поставки, ед.;
| |
| Возможное время задержки поставки – τ (σL), дней. | - определяется эмпирически как наибольшее время, на которое может быть задержана поставка) – τ;
- рассчитывается на основании данных о предыдущих поставках:
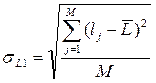 или или 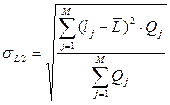
| |
| Интенсивность потребления – d, ед./день | - среднее значение:
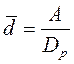 ,
где А – плановый объем потребления.
- прогноз, получаемый при использовании математических методов прогнозирования или по данным отдела маркетинга. ,
где А – плановый объем потребления.
- прогноз, получаемый при использовании математических методов прогнозирования или по данным отдела маркетинга.
| |
| СКО интенсивности потребления – σd | 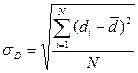
| |
| Потребление за время поставки – d(L), ед. | - можно использовать формулы:
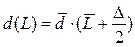 - среднее - среднее
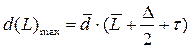 - максимальное
- использовать метод экстраполяции тренда;
- использовать другие методы прогнозирования. - максимальное
- использовать метод экстраполяции тренда;
- использовать другие методы прогнозирования.
|
Окончание табл. 9.6
| № | Показатель | Формула для расчета |
| Страховой запас – Sс, ед. | - вариант 1:
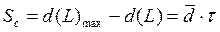 - вариант 2:
- вариант 2:
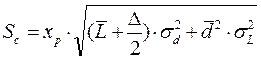 ,
где хp – параметр, соответствующий вероятности отсутствия дефицита. ,
где хp – параметр, соответствующий вероятности отсутствия дефицита.
| |
| ROP | 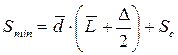
| |
| Размер заказа - Qз, ед. | 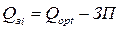 ,
где Qзi – размер заказа в момент времени i;
Qopt – текущий размера заказа; ЗП – запас в пути. ,
где Qзi – размер заказа в момент времени i;
Qopt – текущий размера заказа; ЗП – запас в пути.
| |
| Qopt оптимальная составляющая размера заказа, ед. | См. модель EOQ (формула Харриса-Уилсона) |
Пример 9.3:
Воспользуемся исходными данными из примера 9.1 о параметрах реализации товара «Х» и смоделируем расход запасов с учетом (R; Q)-стратегии для периода в 46 дней.
Рассчитаем значение точки заказа, воспользовавшись соответствующей формулой из табл. 9.6:
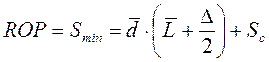 , (9.11)
, (9.11)
где Δ – период контроля состояния запасов на складе, дней. Примем Δ в расчетах равным 1 дню;
Sc – страховой запас, рассчитываемый по формуле:
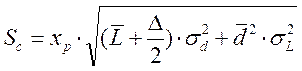 , (9.12)
, (9.12)
Получим:
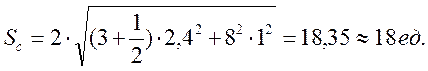
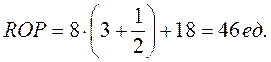
Размер заказов на пополнение запаса будем рассчитывать, используя формулу (9.13) по аналогии с примером 9.2.
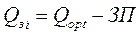 (9.13)
(9.13)
Таким образом, Qз1 = Qopt = 86 ед., где Qopt – оптимальный размер заказа, рассчитанный по формуле (9.6) – см. пример 9.2.
Начальный запас в системе рассчитаем по формуле:
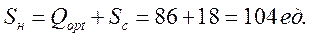 (9.14)
(9.14)
Результаты моделирования действия (R;Q)-стратегии приведены в табл. 9.7. и на рис. 9.11.
Примем в данном примере, что проверки остатка на складе производятся по данным на начало дня. С 1-го по 7-й день включительно запас выше «точки заказа». На начало 8-го дня уровень запаса достиг 39 ед., что меньше «точки заказа» 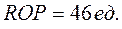 Следовательно, на 8-й день размещается заказ, срок выполнения которого, по аналогии с примерами 9.1 и 9.2 составит 3 дня (L1=3 дн.). Заказ выполняется в течении 8-го, 9-го и 10-го дня и поступает на склад на 11-й день.
Следовательно, на 8-й день размещается заказ, срок выполнения которого, по аналогии с примерами 9.1 и 9.2 составит 3 дня (L1=3 дн.). Заказ выполняется в течении 8-го, 9-го и 10-го дня и поступает на склад на 11-й день.
Следующий момент размещения заказа наступает на 17-й день (начало дня), когда уровень запаса на складе достигает 44 ед. Время выполнения второго заказа L2=4дня (17-й, 18-й, 19-й и 20-й день), т.о. второй заказ поступит на склад на 21 день.
Третий заказ размещается на 27-й день (начало дня), когда уровень запасов достигнет 45 ед., выполняется третий заказ в течении 1-го дня (L3=1) и поступает на склад на 28-й день.
Четвертый заказ размещается на 38-й день (начало дня), когда уровень запасов достигнет 44 ед., выполняется четвертый заказ в течении трех дней (L4=3) и поступает на склад на 41-й день и т.д.
Таблица 9.7
Результаты моделирования действия (R;Q)-стратегии
| Номер дня | Спрос di | Запас на складе, ед. | Дефицит (прогноз), ед. | Заказ | Поставка | ||
| на начало дня | на конец дня | на начало дня | на конец дня | ||||
Окончание табл. 9.7
| Номер дня | Спрос di | Запас на складе, ед. | Дефицит (прогноз), ед. | Заказ | Поставка | |||
| на начало дня | на конец дня | на начало дня | на конец дня | |||||
| И т.д. | … | … | … | … | … | … | … |
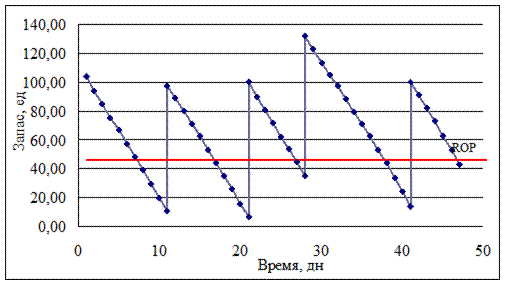
Рис. 9.11. Стратегия с «точкой заказа» и фиксированным размером заказа, (R; Q) - стратегия
Рассмотрим теперь стратегию двух уровней, так называемую (s-S)-стратегию или «минимаксную стратегию» (см. рис. 9.12.). Данная стратегия предполагает, что заявка на пополнение запаса размещается каждый раз по достижении определенного минимального уровня запаса (Smin или s), объем заказа переменный и рассчитывается таким образом, чтобы уровень запаса после поставки достиг «максимально желаемого уровня» (Smax). При этом осуществляется либо непрерывный, либо периодический контроль уровня запаса (Δ→0 или Δ = const). При определении объема заказа учитывается ожидаемый расход запаса за время выполнения поставки (d(L)) и запасы в пути (ЗП). Формулы для расчета параметров «минимаксной» стратегии приведены в табл. 9.8.
|


Smax – максимально желаемый размер запаса, ед.; Sт – текущий запас, ед.; Smin – минимальный уровень запаса, по достижении которого размещается заказ, ед.; Δ – период контроля состояния запасов на складе, дней; Sс – страховой запас, ед.; Qз – размер заказа, ед.; Qп – величина поставки, ед.; d(L) – ожидаемый расход запаса за время поставки, ед.; d(L)факт – фактический расход запаса за время поставки, ед.; tз – момент размещения заказа на поставку; L – время выполнения заказа, дней; tп – момент осуществления поставки; T`- интервал времени между поставками, дней.
Рис. 9.12. Минимаксная стратегия
Таблица 9.8
Параметры «минимаксной» стратегии
| № | Показатель | Порядок определения показателей | |
| Детерминированный вариант | Стохастический вариант | ||
| Интервал между проверками уровня запаса – Δ | - определяется в соответствии с условиями работы склада компании и уровнем автоматизации; может быть непрерывным (в режиме on-line) в случае соответствующего информационного обеспечения склада (Δ→0); может быть периодическим, например, через день, или 1 раз в неделю (Δ = const). | - определяется в соответствии с условиями работы склада компании и уровнем автоматизации; может быть непрерывным (в режиме on-line) в случае соответствующего информационного обеспечения склада (Δ→0); может быть периодическим, например, через день, или 1 раз в неделю (Δ = const). | |
| Время выполнения поставки – L, дней | - обычно указывается в договоре на поставку (среднее значение); | - определяется статистически на основе данных по прошлым поставкам:
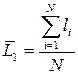 или или 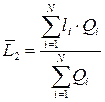 ,
где li – значение времени выполнения i-й поставки, дней;
Qi – величина i-й поставки, ед.; ,
где li – значение времени выполнения i-й поставки, дней;
Qi – величина i-й поставки, ед.;
|
Продолжение табл. 9.8
| № | Показатель | Порядок определения показателей | |
| Детерминированный вариант | Стохастический вариант | ||
| Возможное время задержки поставки – τ (σL), дней. | - определяется эмпирически как наибольшее время, на которое может быть задержана поставка) – τ; | - рассчитывается на основании данных о предыдущих поставках:
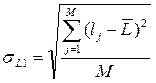 или или 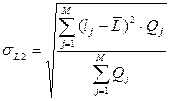
| |
| Интенсивность потребления – d, ед./день |
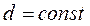 или
или
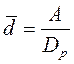
| - среднее значение:
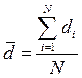 ,
где di – расход в i-й момент времени; N – объем выборки
- прогноз, получаемый при использовании математических методов прогнозирования или по данным отдела маркетинга. ,
где di – расход в i-й момент времени; N – объем выборки
- прогноз, получаемый при использовании математических методов прогнозирования или по данным отдела маркетинга.
| |
| СКО интенсивности потребления – σd | - среднее квадратическое отклонение от среднего расхода: 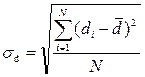
|
Продолжение табл. 9.8
| № | Показатель | Порядок определения показателей | |
| Детерминированный вариант | Стохастический вариант | ||
| Потребление за время поставки – d(L), ед. | - можно использовать формулы:
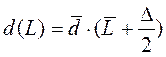 - среднее - среднее
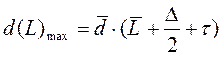 - максимальное - максимальное
| - использовать метод экстраполяции тренда; - использовать другие методы прогнозирования. | |
| Страховой запас – Sс, ед. |
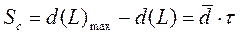
| 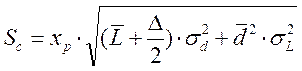 ,
где хp – параметр, соответствующий вероятности отсутствия дефицита. ,
где хp – параметр, соответствующий вероятности отсутствия дефицита.
| |
| Smin – пороговый уровень запаса, ед. | 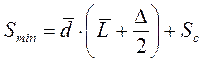
| 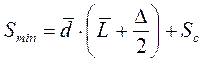
| |
| Максимально желаемый объем запаса– Smax , ед. | - вариант 1:
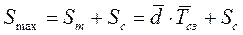 ,
где ,
где 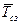 - среднее значение периода времени между смежными заказами, дней. - среднее значение периода времени между смежными заказами, дней.
| 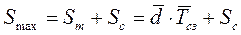 ,
где ,
где 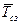 - среднее значение периода времени между смежными заказами, дней. - среднее значение периода времени между смежными заказами, дней.
|
Окончание табл. 9.8
| № | Показатель | Порядок определения показателей | |
| Детерминированный вариант | Стохастический вариант | ||
| Максимально желаемый объем запаса– Smax , ед. |
- вариант 2:
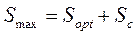 ,
где Sopt – оптимальный размер запаса, рассчитанный с помощью модели EOQ. ,
где Sopt – оптимальный размер запаса, рассчитанный с помощью модели EOQ.
| ||
| Размер заказа - Qз, ед. | 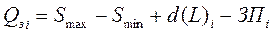 ,
где Qзi – размер заказа в момент времени i;
Smin – пороговый (минимальный) уровень запаса;
ЗПi – запас в пути на момент времени i. ,
где Qзi – размер заказа в момент времени i;
Smin – пороговый (минимальный) уровень запаса;
ЗПi – запас в пути на момент времени i.
| 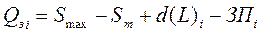 ,
где Qзi – размер заказа в момент времени i;
Sm – текущий запас, который ≤ пороговому (минимальному) уровеню запаса;
ЗПi – запас в пути на момент времени i. ,
где Qзi – размер заказа в момент времени i;
Sm – текущий запас, который ≤ пороговому (минимальному) уровеню запаса;
ЗПi – запас в пути на момент времени i.
|
Пример 9.4:
Воспользуемся исходными данными из примера 9.1 о параметрах реализации товара «Х» и смоделируем действие (s; S)-стратегии для периода в 46 дней.
Расчет страхового запаса осуществим по формуле:
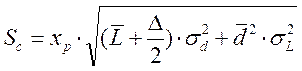 (9.15)
(9.15)
Получаем:
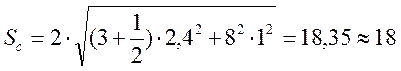
Верхнюю границу уровня запасов (Smax) будем рассчитывать по формуле:
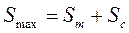 , (9.16)
, (9.16)
где Sт – текущий запас. В качестве текущего запаса целесообразно использовать величину оптимального размера заказа (Qopt). Величина оптимального размера заказа была рассчитана в примере 9.2. Qopt = 86 ед.
Таким образом, начальный (максимальный) запас в системе будет: 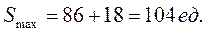
Нижняя граница уровня запасов (Smin) рассчитывается по формуле:
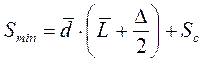 (9.17)
(9.17)
Дата добавления: 2016-01-07; просмотров: 2515;
