Откорректированная формула Феттера

Некорректность расчета по формуле (8.1) состоит в том, что для разных 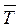подставляется одно и то же значение s_Т.

Допустим, что статистические параметры, характеризующие ежедневный расход (или объем продаж), 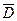и σ_D – постоянны и не зависят от продолжительности цикла Т; закон распределения ежедневных продаж – нормальный. Для продолжительности цикла, подчиняющегося нормальному закону, среднее значение равно 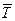, а среднее квадратическое отклонение:

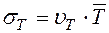, (8.2)

где υ_т – коэффициент вариации, определенный на основе статистической обработки для базовой выборки.

Например, если статическая информация собрана для базового уровня цикла заказа с параметрами 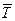=10 дней, σ_т=2 дня и υ_т=0,2, то для цикла с 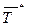=20 дней, соответственно σ_Т=0,2·20=4 дня.

Таким образом, формула (8.1) может быть записана в виде:

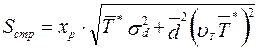, (8.3)

где 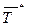- среднее значение продолжительности цикла заказа, отличное от базового уровня.

Пример 8.1:

Пусть средняя потребность в продукции ( 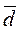) составляет 5 ед./день. Спрос на продукцию подчинен нормальному закону распределения с СКО (σ_d) = 1 ед. и коэффициентом вариации (ν_d) = 0,2. Среднее время выполнения 1 заказа поставщиком составляет 10 дней и также подчинено нормальному закону распределения с коэффициентом вариации 0,3 (ν_T) и среднеквадратическим отклонением – 3 дня (σ_T). Вероятность отсутствия дефицита 98%, т.е. x_p ≈ 2. Необходимо рассчитать величину страхового запаса с учетом возможного увеличения среднего срока поставки ( 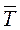) до 30 дней без изменения закона распределения.

Воспользуемся формулой (8.1) и рассчитаем страховой запас при 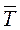=10 и 30 дней.

Для 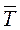=10 дней получаем:

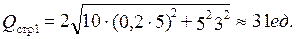
Для 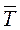=30 дней получаем:

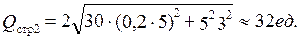
Теперь воспользуемся корректированным вариантом формулы (8.3). Для 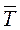=30 дней получим:

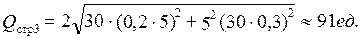
Результаты проведенных расчетов показывают, что при изменении среднего времени выполнения заказа корректированная формула (8.3) дает результат, отличный от стандартной формулы (8.1). Это происходит потому, что при изменении времени выполнения заказа в классической формуле Феттера не учли соответствующее изменение СКО, которое предусмотрено в корректированной формуле.

Опыт показывает, что расчет по формулам (8.1) и (8.3) подходит для тех случаев, когда для управления запасами применяется периодическая стратегия (стратегия с постоянной периодичностью размещения заказа).

Рис. 8.3. Определение потребности в страховом запасе при различных типах стратегий управления запасами (А – периодическая стратегия; В – стратегия с точкой заказа)

При использовании периодической стратегии управления запасами (рис. 8.3.А) заказ на пополнение запаса делается в заранее определенные моменты времени, при этом вариация спроса может привести к ситуации, когда дефицит будет наблюдаться уже на момент размещения заказа. Кроме того, дефицит будет накапливаться за время выполнения заказа. Поэтому при расчете страхового запаса здесь необходимо учитывать отклонения в спросе за все время логистического цикла (T).

При использовании стратегий управления запасами с точкой заказа (ROP), когда заказ на пополнение запаса делается по достижении определенного уровня запаса на складе, дефицит на момент заказа маловероятен, а при непрерывном контроле за уровнем заказа – вообще исключен. Поэтому при расчете страхового запаса здесь необходимо учитывать отклонения в спросе только за время выполнения заказа (L):

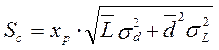(8.4)

или

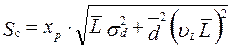, (8.5)

где 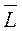- среднее значение времени выполнения заказа (поставки).

υ_L – коэффициент вариации для случайной величины «время выполнения заказа».

Также следует отметить, что формула Феттера и ее модификации, приведенные выше, выведены из условия нормального закона распределения случайных величин спроса и времени выполнения заказа (либо времени всего логистического цикла). Для других законов распределения требуются иные подходы для расчета страхового запаса, которые пока находятся на стадии разработки.

Вопросы и задания для самостоятельной работы

1. С какой целью формируется страховой запас?

2. Какие ошибки могут возникнуть при расчете страхового запаса?

3. Рассчитайте величину страхового запаса при 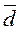=10 ед., σ_d=2,54; υ_т=0,2, , T = 8 дней; вероятность отсутствия дефицита = 0,95.

4. Рассчитайте величину страхового запаса при 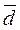= 25 ед. (средний расход), σ_d=5 (СКО среднего расхода); υ_т= 0,1 (коэффициент вариации для времени поставки), T = 18 дней (время поставки); уровень обслуживания = 90%.

5. Рассчитайте величину страхового запаса при 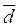= 15 ед. (средний расход), υ_d= 0,3 (коэффициент вариации среднего расхода); σ_т= 3 (СКО времени поставки), T = 10 дней (время поставки); уровень обслуживания = 94%.