Сущность задачи и основные подходы к решению
В предыдущих разделах при выводе формул для расчета оптимального размера заказа считалось, что каждый вид продукции не зависит от остальных и он хранится на складе самостоятельно. Однако, для промышленных предприятий, а также предприятий розничной и оптовой торговли условия независимости видов продукции друг от друга могут быть нарушены. Основными причинами возникновения взаимосвязи между N видами продукции, поставляемой на склад, являются следующие ограничения:
· максимальный размер капитала В, который предполагается вложить в запасы;
· площадь (объем) склада, где размещаются одновременно N видов продукции;
· верхний предел общего числа заказов за определенный период и др.
Помимо указанных одиночных ограничений могут возникнуть ситуации, когда требуется соблюдение нескольких из них или всех одновременно. Например, для промышленных предприятий рассматриваются случаи ограничения, налагаемые планом выпуска продукции и размером капитала. Могут встретиться варианты, когда имеется ограничение на число заказов, подаваемых в течение года, и ограничение на максимальные капиталовложения в любой момент времени.
Рассмотрим подробнее вариант задачи, когда закупаются материальные ресурсы из нескольких источников и существуют ограничения на бюджет закупки.
На первом этапе рассчитываются оптимальные партии поставок soi по каждому i- му виду продукции (i=1,…N) по классической формуле Харриса-Уилсона.
На втором этапе сравниваются затраты, связанные с запасами продукции и капиталом В, выделенном на приобретение продукции:
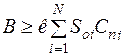 , (7.1)
, (7.1)
где к – коэффициент, введенный для учета неравномерности поступления i-ых видов продукции; 0<к≤1. В работах [8, 20] принято к=0,5.
Если неравенство (7.1) соблюдается, то поставки осуществляются в объемах, рассчитанных на первом этапе. Соответственно, переменные затраты на выполнение заказа и хранение при многопродуктовой поставке определяется по формуле
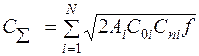 (7.2)
(7.2)
Третий этап, когда неравенство (7.1) не соблюдается. Для расчета оптимальных значений Soi применяется метод множителей Лагранжа.
В качестве критерия оптимизации принимается минимум общих переменных затрат С∑, включающих затраты на выполнение заказов Сз и затраты на хранения запасов на складе Схр:
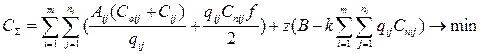 , (7.3)
, (7.3)
где i - индекс, указывающий порядковый номер поставщика, i = 1…m;
j - индекс, указывающий порядковый номер вида продукции, заказываемого у i-го поставщика, j = 1…ni;
m - количество поставщиков;
ni - количество видов продукции, заказываемых у i-го поставщика;
Aij – потребность в заказываемом продукте;
qij – искомая величина заказа, ед.;
Спij – цена единицы продукции;
f – доля от цены Спij, приходящейся на затраты по хранению единицы продукции;
Coij – затраты на транспортировку (принимаются постоянными для партии);
Cij – составляющая затрат на выполнение заказа, которая зависит от объема выполняемых на складе операций при формировании заказа;
B – максимальный размер капитала, который предполагается вложить в запасы;
k – коэффициент, введенный для учета неодновременного заказа различных видов продукции, 0<k<=1;
z – неопределенный множитель Лагранжа. Для расчета z можно воспользоваться формулой
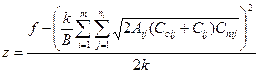 (7.4)
(7.4)
Параметры модели оптимального заказа в условиях финансовых ограничений и при наличии нескольких источников поставок могут быть найдены по следующим формулам:
оптимальный размер заказа
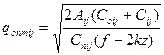 , (7.5)
, (7.5)
минимальные переменные издержки
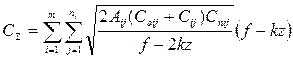 , (7.6)
, (7.6)
количество заказов
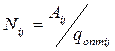 , (7.7)
, (7.7)
периодичность размещения заказов
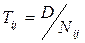 , (7.8)
, (7.8)
где D – продолжительность рассматриваемого периода.
общие издержки:
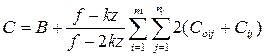 (7.9)
(7.9)
Теперь рассмотрим вариант решения задачи, когда требуется организовать совместную отправку материальных ценностей от каждого поставщика в условиях ограничения на финансовые ресурсы.
Учет ограничения производится при помощи формулы:
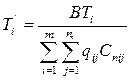 , (7.10)
, (7.10)
где Ti - интервал между одновременными поставками ni видов продукции от i-го поставщика.
Если T’i≥Ti, то параметры таких поставок рассчитываются по следующим формулам:
количество заказов:
Ni = D/Ti (7.11)
оптимальный размер заказа:
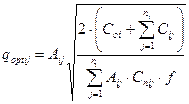 (7.12)
(7.12)
минимальные переменные издержки:
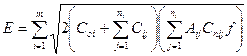 (7.13)
(7.13)
общие затраты:
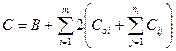 (7.14)
(7.14)
Если T’i<Ti, тогда в качестве расчетного периода принимается T’i и производится корректировка:
оптимального размера заказа:
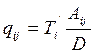 (7.15)
(7.15)
числа поставок:
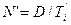 (7.16)
(7.16)
минимальных переменных издержек:
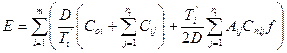 (7.17)
(7.17)
общих затрат:
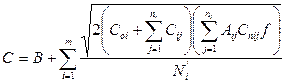 (7.18)
(7.18)
Пример 7.1:
Рассмотрим систему поставок запасных частей для автотранспортного предприятия «Х». Поставщики и поставляемая ими номенклатура запасных частей представлены на схеме (рис. 7.1) и в табл. 7.1.
Таблица 7.1
Список поставщиков и поставляемой ими продукции
| № | Продукция | Поставщик |
| 1/1 | Барабаны тормозные Икарус задние | ООО "Июль" |
| 1/2 | Барабаны тормозные Икарус передние | |
| 1/3 | Барабаны тормозные ЛиАЗ 5256 (RABA) | |
| 2/1 | Мотор вентилятора отопителя (с крыльчаткой)№42.378 24v(улитки) | ООО "Бусторг" |
| 2/2 | Мотор редуктора стеклоочистителя ЛиАЗ-5256 правый | |
| 3/1 | Клин с роликами 5256-3501110 | ЗАО "Август" |
| 3/2 | Упор колодки 5656-3501049 |

Рис. 7.1. Поставщики и поставляемые ими позиции номенклатуры
Исходные данные для примера приведены в табл. 7.2. Затраты на оформление заказа взяты равными 960 руб. (минимальная стоимость доставки по городу на автомобиле марки «Газель»), при этом издержки на хранение рассчитываются через процент от стоимости единицы продукции, который условно считается равным 20 %. Затраты на комплектование принимаем равными 5 % от цены единицы продукции. Считаем, что существует ограничение на бюджет и оно равно 300 000 рублей.
Рассчитанные величины оптимальных размеров партий поставок, их количества и периодичности, а также минимальные переменные и общие издержки для различных вариантов организации многономенклатурных поставок в условиях финансовых ограничений приведены в табл. 7.3 и 7.4.
Таблица 7.2
Исходные данные
| Параметры | Номер поставщика / номер продукта | |||||||
| 1/1 | 1/2 | 1/3 | 2/1 | 2/2 | 3/1 | 3/2 | ||
| Годовой спрос A, ед. | ||||||||
| Стоимость единицы продукции Сп, руб. | ||||||||
| Затраты на оформление заказа Co, руб. | ||||||||
| Затраты на комплектование партии Ci, руб. | ||||||||
| Параметр f | 0,2 | |||||||
| Коэффициент k | ||||||||
| Ограничение на бюджет - B, руб. | ||||||||
| Множитель Лагранжа – z, рассчитывается по формуле (7.4) | -0,22 | |||||||
Таблица 7.3
Вариант: независимые отправки с ограничением на бюджет
| Параметры | Номер поставщика / номер продукта | Сумма | ||||||
| 1/1 | 1/2 | 1/3 | 2/1 | 2/2 | 3/1 | 3/2 | ||
| Размер партии поставки qо, ед. | - | |||||||
| Стоимость запасов qo*Сп, руб. | ||||||||
| Количество поставок Nij | - | |||||||
| Периодичность поставки Ti, дн. | - | |||||||
| Переменные затраты, руб. | ||||||||
| Общие затраты | 309833,3 |
Таблица 7.4
Вариант: одновременные отправки c ограничением на бюджет
| Параметры | Номер поставщика / номер продукта | Сумма | ||||||
| 1/1 | 1/2 | 1/3 | 2/1 | 2/2 | 3/1 | 3/2 | ||
| Размер партии поставки qо, ед. | - | |||||||
| Стоимость запасов qo*Сп, руб. | ||||||||
| Количество поставок Nij | - | |||||||
| Периодичность поставки Ti, дн. | ||||||||
| Переменные затраты, руб. | ||||||||
| Общие затраты | 305758,4 |
Вопросы и задания для самостоятельной работы
1. В чем заключается сущность «многопродуктовой» модели управления запасами?
2. Назовите возможные варианты организации поставок многономенклатурной продукции от нескольких поставщиков.
3. В чем состоит методика использования «множителя Лагранжа» при решении «многопродуктовой» задачи управления запасами?
4. Каковы основные причины возникновения взаимосвязи между различными видами продукции в процессе ее поставки потребителю?
5. Для исходных данных, представленных в табл. 7.5, необходимо рассчитать оптимальные объемы заказа продукции в условиях ограничения на бюджет (В=6000 руб.). При решении задачи рекомендуется воспользоваться многопродуктовой моделью с возможностью совместных отправок. При решении задачи принимать f = 0,2 и D =365 дней.
Таблица 7.5
Исходные данные для решения задачи
| Параметры, показатели | Вид продукции | ||
| Потребность в заказываемом продукте Аi, ед. Цена единицы продукции Сni , руб. Затраты на выполнение одного заказа С0i, руб. |
Дата добавления: 2016-01-07; просмотров: 1121;
