Модели расчета страхового запаса
Формула Феттера
Классическая модель расходования и пополнения запасов является идеальной при полностью детерминированных параметрах управления запасами. Большая часть практических ситуаций отличается от идеальной схемы; в них присутствует неопределенность, вызванная различными причинами, но главным образом случайным характером ежедневного спроса dj и продолжительности логистического цикла Ti. Случайность основных параметров поставок и спроса, а также логистические риски являются причинами создания страховых запасов.
Анализ различных источников позволил сформулировать следующие положения [32]:
1. Реализация текущего запаса в общем случае представляет собой дискретный, невозрастающий случайный процесс, отражающий нестационарность и стохастичность спроса (А, рис.8.1).
2. Поставки являются случайными величинами и подчиняются определенным законам распределения (В, рис.8.1).
3. Момент окончания каждой реализации случаен, но в одних случаях остаточный запас в момент поставки больше нуля, в других - равен нулю. При отсутствии страхового запаса, последняя ситуация означает наступление дефицита (D, рис.8.1). При наличии страхового запаса данная ситуация может быть названа «псевдодефицитом», поскольку спрос удовлетворяется за счет страхового запаса. С вероятностной точки зрения функция распределения текущего запаса (в момент поставки) будет подчиняться усеченному нормальному закону распределения либо законам распределения для положительных случайных величин (С, рис.8.1).
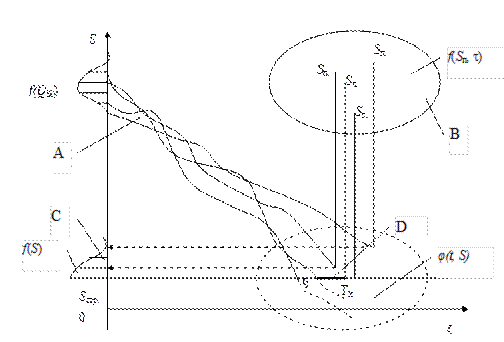
Рис.8.1. Модель расхода и пополнения запасов с учетом неопределенности спроса и продолжительности цикла заказа [32]
4. При расчете параметров системы управления запасами используются оптимальная величина заказа (формула Харриса-Уилсона (5.6)) и время между заказами формула (5.8). Однако сама формула получена при идеальных условиях, что накладывает дополнительные ограничения на возможности ее использования при управлении заказами. Помимо этого, расчет по формуле Харриса-Уилсона не всегда возможен ввиду трудности и отчасти условности определения значений, входящих в нее величин, например, годовой объем потребления, затраты на поставку и хранение и т.д.
5. Если в момент времени tj суммарный ежедневный расход 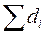 достигает начального запаса на складе Sо, т.е. возникает ситуация дефицита, то предполагается, что неудовлетворенные заявки продолжают накапливаться до случайного момента Тк - времени поступления нового заказа. Таким образом, при
достигает начального запаса на складе Sо, т.е. возникает ситуация дефицита, то предполагается, что неудовлетворенные заявки продолжают накапливаться до случайного момента Тк - времени поступления нового заказа. Таким образом, при 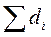 ≥So речь идет не о реальном, а о прогнозируемом процессе накопления заявок на интервале ΔT = Tk - Tj. Случайные накопленные величины дефицита используются для оценки страхового запаса.
≥So речь идет не о реальном, а о прогнозируемом процессе накопления заявок на интервале ΔT = Tk - Tj. Случайные накопленные величины дефицита используются для оценки страхового запаса.
Для расчета величины страхового запаса в условиях неопределенности может быть использована формула Феттера:
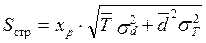 , (8.1)
, (8.1)
где xp– параметр нормального закона распределения, соответствующий вероятности отсутствия дефицита продукции на складе P(х) (табл. 3.1, рис. 8.2)
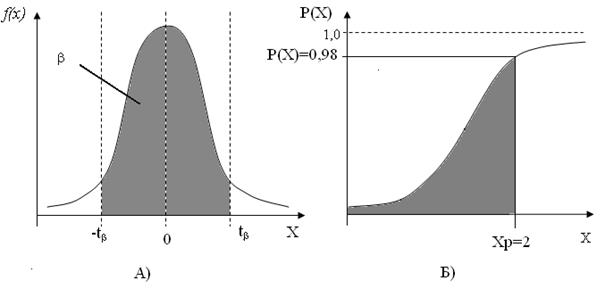
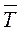 - среднее значение продолжительности функционального цикла (период времени между поставками);
- среднее значение продолжительности функционального цикла (период времени между поставками);
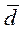 - среднесуточный расход запаса;
- среднесуточный расход запаса;
σТ, σd – соответственно средние квадратические отклонения случайных величин T и d.
Часто наравне с коэффициентом хр (табл. 3.1) в формуле расчета страхового запаса использован коэффициент tβ – табл. 8.1.
Таблица 8.1
Определение параметра tβ в зависимости от желаемого уровня обслуживания клиентов
| Уровень обслуживания с вероятностью отсутствия дефицита Р(tβ), % | Коэффициент tβ |
| 84,1 | 1,0 |
| 90,3 | 1,3 |
| 94,5 | 1,6 |
| 97,7 | 2,0 |
| 98,9 | 2,3 |
| 99,5 | 2,6 |
| 99,9 | 3,0 |
А) плотность распределения;
Б) функция распределения.
Рис. 8.2 Нормальный закон распределения
В различных источниках предлагается несколько вариантов соотношения коэффициента хр и tβ для страхового запаса и уровня обслуживания исходя либо из интегральной функции распределения, либо из плотности (табл. 8.2).
Таблица 8.2
Соотношение уровня обслуживания и величины множителя
для страхового запаса
| Уровень обслуживания с вероятностью отсутствия дефицита Р(x) | Значение коэффициента хр | Уровень обслуживания с заданной вероятностью попадания в границы Р(tв), % | Значение коэффициента хр |
| 0,5 | - | - | |
| 0,55 | 0,125 | - | - |
| 0,6 | 0,253 | - | - |
| 0,65 | 0,385 | - | - |
| 0,7 | 0,525 | - | - |
| 0,75 | 0,675 | - | - |
| 0,8 | 0,842 | - | - |
| 0,85 | 1,037 | - | - |
| 0,9 | 1,28 | 0,8 | 1,282 |
| 0,92 | 1,405 | 0,84 | 1,404 |
| 0,94 | 1,555 | 0,88 | 1,554 |
| 0,95 | 1,645 | 0,9 | 1,643 |
| 0,96 | 1,75 | 0,92 | 1,75 |
| 0,98 | 2,05 | 0,96 | 2,053 |
| 0,99 | 2,3 | 0,98 | 2,325 |
| 0,999 | 3,1 | 0,998 | 3,29 |
Проведенный нами вычислительный эксперимент позволил сделать следующий вывод:
Для всех теоретических значений вероятности отсутствия дефицита Р(х) и, соответственно, коэффициентов хp, наблюдается превышение ожидаемого количества дефицитных реализаций над практически наблюдаемым, т.е. уровень надежности выше, чем заявлен.
Анализ соотношения экспериментального уровня отсутствия дефицита и теоретически заявленного Р(tв) показал значительное превышение теоретического значения отсутствия дефицитных реализаций над результатами моделирования.
По итогам экспериментов, значения вероятностей отсутствия дефицита для множителя хр наиболее соответствует теоретически заявленному уровню.
Дата добавления: 2016-01-07; просмотров: 2588;
