Многономенклатурные поставки по системе кратных периодов
В 1966 г. профессор Ю.И. Рыжиков [38] предложил стратегию организации многономенклатурных поставок по системе кратных периодов.
Система кратных периодов предполагает, что по крайней мере одна номенклатурная позиция заказывается в каждом базисном периоде (Т), а остальные позиции поставляются с периодичностями, кратными, базисному периоду ( k·Т , где k=1,2,3,…).
Рассмотрим простой пример поставки 2 видов продукции. Допустим, что одна из позиций номенклатуры имеет наименьшую периодичность поставки Т=10 дней. Это означает, что последующие поставки будут производиться с указанной периодичностью и время поставки будет равно 2Т= 20 дней, третьей 3Т= 30 дней и т.д.
Вторая позиция номенклатуры, поставки которой будут производиться согласно стратегии кратных периодов, имеет периодичность 2Т= 20 дней. Соответственно, вторая поставка будет произведена на 40 день и т.д. В результате совмещения поставок двух видов продукции получим следующую последовательность: через 10 дней поставляется первый вид продукции, на 20 день оба вида продукции, на 30 день – первый вид, на 40 день – оба вида и т.д.
В системе кратных периодов оптимальный период группирования (базисный период) определяется по формуле [27, 38]:
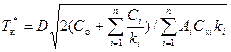 (6.15)
(6.15)
Данному периоду соответствуют минимальные затраты:
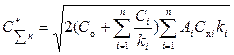 (6.16)
(6.16)
На основе 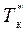 определяются величины поставок
определяются величины поставок 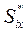 и количество поставок Nг за плановый период (или год).
и количество поставок Nг за плановый период (или год).
Методика организации поставок по кратным периодам состоит из нескольких основных этапов:
1. Позиции номенклатуры ранжируются по возрастанию величин показателей 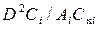 , то есть с учетом периодичности независимой поставки каждой позиции номенклатуры Тi .
, то есть с учетом периодичности независимой поставки каждой позиции номенклатуры Тi .
2. Выбираются начальное приближение для кратного периода; за основу принимается первое значение ранжированного ряда (минимальный период времени при независимых поставках):
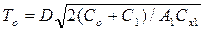 (6.17)
(6.17)
3. Рассчитывается набор коэффициентов 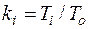 , с помощью которых производится формирование базового варианта групп различной кратности.
, с помощью которых производится формирование базового варианта групп различной кратности.
4. Каждая позиция номенклатуры закрепляется за определенной группой.
По формулам (6.15) и (6.16) для базового варианта рассчитываются показатели 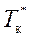 и
и 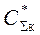 и затем с использованием итерационной процедуры (путем перебора и размещения позиций номенклатуры в группах различной кратности) осуществляется поиск оптимального варианта по критерию минимума суммарных затрат
и затем с использованием итерационной процедуры (путем перебора и размещения позиций номенклатуры в группах различной кратности) осуществляется поиск оптимального варианта по критерию минимума суммарных затрат 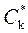 .
.
Выбор То можно осуществить по множеству номенклатур, заказываемых в каждом периоде, при этом первые j позиции номенклатуры из упорядоченного множества заказываются одновременно. Расчетная формула записывается в виде:
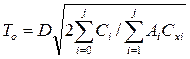 (6.18)
(6.18)
Присоединение к первой группе следующих позиций номенклатуры целесообразно при соблюдении неравенства:
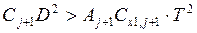 (6.19)
(6.19)
При подстановке (6.18) в формулу (6.19) условие прекращения накопления группы записывается в виде:
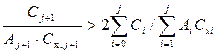 (6.20)
(6.20)
Проверка рекуррентного соотношения начинается со второй позиции номенклатуры, при этом в правой части подставляются значения 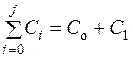 и
и 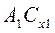 . При выполнении условия (6.20) для всех последующих позиций i > j вычисляется оптимальная периодичность Ti и по отношению Ti / To – начальная кратность.
. При выполнении условия (6.20) для всех последующих позиций i > j вычисляется оптимальная периодичность Ti и по отношению Ti / To – начальная кратность.
Пример 6.3:
В табл. 6.5 приведены исходные данные о четырех видах продукции. Требуется выбрать наилучшую стратегию поставок (при С0=18 у.е.).
Таблица 6.5
Исходные данные и результаты расчета при независимых
поставках
| Вид продукции | Ai, ед. | Сi, у.е | Сo+ Сi, у.е. | СXi, у.е. | Si, ед. | Ti дни | С* ∑i у.е. | ki | Базовый вариант ki |
| 1,5 1,0 0,5 0,5 | 37,7 54,1 76,6 | 1,43 2,03 4,24 | |||||||
| Сумма |
Для проведения расчетов воспользуемся табл. 6.6, в которой обобщены формулы для трех вариантов многономенклатурных поставок:
- независимые поставки каждой позиции номенклатуры;
- одновременная поставка всех позиций;
- одновременная поставка по системе кратных периодов.
Таблица 6.6
Формулы для расчета показателей многономенклатурного заказа
| Наименование показателя | Независимые поставки | Одновременно по всей номенклатуре | Система кратных периодов |
| Время выполнения заказа Тi, дни | 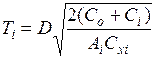
| 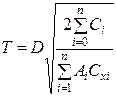
| 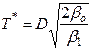
|
| Число заказов за период D | 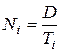
| 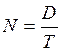
| 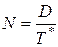
|
Окончание табл. 6.6
Формулы для расчета показателей многономенклатурного заказа
| Наименование показателя | Независимые поставки | Одновременно по всей номенклатуре | Система кратных периодов |
| Объем заказа, Si | 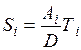
| 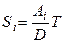
| 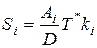
|
| Минимальные суммарные затраты за период D С∑ | 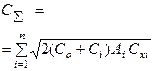
| 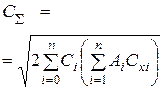
| 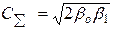
|
Примечание: 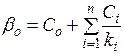 ; ; 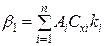
|
На первом этапе рассчитаем показатели при независимых поставках каждой позиции номенклатуры (табл.6.5).
На втором этапе рассчитаем показатели при одновременной многономенклатурной поставке:
- периодичность поставки:
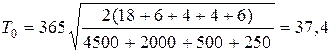 день,
день,
- количество:
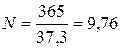 ,
,
- минимальные суммарные затраты:
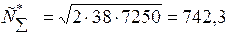 у.е.,
у.е.,
- величины поставок каждой позиции номенклатуры (по формуле (6.7)):
S1=307 ед.; S2=204 ед.; S3=102 ед.; S4=51 ед.
На третьем этапе, для предварительно рассчитанных показателей независимых поставок (первый этап) проводится их ранжирование и определяются коэффициенты кратности ki, относительно приближения Т=37,7 дня, определенного на первом этапе.
На основании ki выберем базовый вариант кратности поставок: первый и второй вид продукции – k=1; третий вид – k=2; четвертый вид – k=4.
Рассчитаем составляющие формул (6.31), (6.32) для базового варианта кратных периодов:
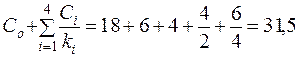 у.е.
у.е.
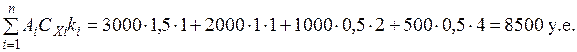 Тогда, оптимальный период:
Тогда, оптимальный период:
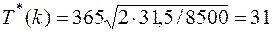 ,4 день
,4 день
минимум суммарных затрат:
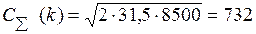 у.е.
у.е.
На рис. 6.2 приведена диаграмма, отражающая различные варианты многономенклатурных поставок, в частности, стратегию кратных поставок для базового варианта (ki: 1,1,2,4).
Для расчета величин поставок каждого вида продукции по системе кратных периодов воспользуемся формулой:
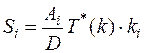 (6.21)
(6.21)
Так, для продукции первого вида находим:
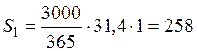 ед.
ед.
Соответственно, для остальных видов получим S2=S3=S4=172 ед.
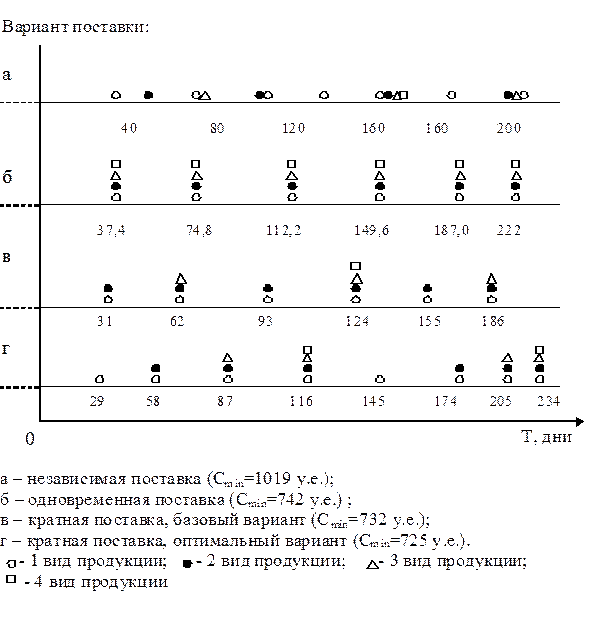 Рис.6.1. Различные варианты многономенклатурных поставок
Рис.6.1. Различные варианты многономенклатурных поставок
В табл. 6.7 приведены результаты расчета оптимальных периодов и минимальных суммарных затрат для различных стратегий кратных периодов при многономенклатруных поставках. Из табл. 6.7 следует, что при организации поставок в соответствии с пятой стратегией наблюдается наименьшее значение минимальных затрат С∑min=725 у.е.
Таблица 6.7
Результаты расчета показателей многономенклатурных поставок для различных стратегий
| Номер стратегии | Коэффициенты кратности | 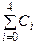 у.е.
у.е.
| 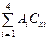 у.е.
у.е.
| Т*(k) дни | 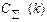 у.е.
у.е.
| |||
| k1 | k2 | k3 | k4 | |||||
| (базовая) | 31,5 | 31,4 | ||||||
| 29,5 | 27,4 | |||||||
| 30,4 | ||||||||
| 31,0 | ||||||||
| 28,8 | 29,2 |
Вопросы и задания для самостоятельной работы
1. В чем заключается специфика многономенклатурной модели?
2. Какие ограничения могут быть учтены в многономенклатурной модели и каким образом?
3. Приведите аргументы в пользу объединения нескольких номенклатур в одну отправку.
4. Приведите примеры комплементарных товаров (дополняющих друг друга, совместно реализуемых), которые целесообразно поставлять совместно.
5. В чем состоят особенности «многопродуктовой» модели?
6. В чем заключается сущность модели организации поставок многономенклатурной продукции по системе кратных периодов?
7. Каков порядок действий при организации поставок многономенклатурной продукции по системе кратных периодов?
8. Для исходных данных из табл. 6.8 необходимо произвести расчет параметров многономенклатурной модели для случая одновременных отправок. Необходимо также сопоставить данные по затратам при многономенклатурных отправках с данными по затратам при независимых отправок продукции и определить экономический эффект от многономенклатурных отправок.
9. Для исходных данных из табл. 6.8. необходимо подобрать оптимальный вариант многономенклатурных отправок по системе кратных периодов.
Таблица 6.8
Исходные данные для решения задачи
| Вид продукции | Аi, ед. | Затраты на выполнение заказа, руб. | Затраты на хранение Сxi, руб./ед. | |
| Со | Сi | |||
| Суммы | - | - | - |
7. модель eoq в условиях финансовых ограничений и наличии нескольких источников поставок*
Дата добавления: 2016-01-07; просмотров: 1732;
