Построение ядра сечения
Рассмотрим некоторое сечение (рис.19.14).

рис.19.14 рис.19.15
Если точка приложения силы F находится на границе ядра сечения, то зоны растяжения не будет. Бесконечно малое удаление силы от ядра приведет к тому, что появится зона растяжения, значит для точек границы ядра нейтральная линия касается нашего сечения.
Следовательно, для построения ядра надо рассмотреть всевозможные касательные к сечению и найти для этих случаев точки приложения силы. Соединив затем эти точки, найдем ядро сечения.
Примечание:
Если контур состоит из прямых отрезков, то задача построения ядра сильно облегчается.
Рассмотрим процедуру построения ядра сечения.
Запишем уравнение I-ой нейтральной линии (рис.19.15). Это уравнение, проходящее через две точки 1-2:
 . (19.9)
. (19.9)
Уравнение (19.9) должно совпадать с уравнением (19.8). Таким образом, уравнение (19.9) известно, и известны 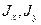 , надо найти
, надо найти 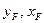 .
.
Для этого сначала полагаем x=0. Из соотношения (19.9) находим y, подставляем эти х, у в уравнение (19.8) и находим уF.
Для отыскания хF полагаем y = 0. Из формулы (19.9) находим x, подставляем эти х и у в уравнение (19.8) и находим хF.
Важное примечание. Рассмотрим угловую точку В. Через точку В можно провести бесконечно много касательных.
Однако все прямые, проходящие через точку В, описываются уравнением, которое удовлетворяется при подстановке  . Подставим их в уравнение (19.8):
. Подставим их в уравнение (19.8):
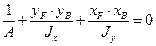 .
.
Поскольку  ,
, 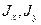 - это известные числа, то в результате получим
- это известные числа, то в результате получим
 ,
,
где a,b,c – постоянные. Это есть уравнение прямой, на которой лежат точки границы ядра.
Таким образом, при переходе от стороны BC к стороне BD, искать 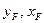 не нужно, а нужно просто соединить прямой две точки границы ядра, которые получены для BC и BD.
не нужно, а нужно просто соединить прямой две точки границы ядра, которые получены для BC и BD.
Рассмотрим примеры. Найдем ядро сечения для прямоугольника.

рис.19.16
Для I-ой нейтральной линии уравнение прямой (19.9) имеет вид:
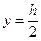 . (19.10)
. (19.10)
Для (19.8) имеем:
 ,
, 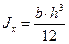 ,
, 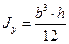 .
.
Тогда (19.8) примет вид:
 .
.
Умножая на 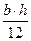 получим:
получим:
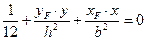 . (19.11)
. (19.11)
Полагаем сначала х = 0. Тогда из (19.10) вытекает, что 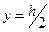 . Подставляя в (19.11) получаем:
. Подставляя в (19.11) получаем:
 .
.
Найдем хF. Поскольку в (19.10) можно принимать лишь 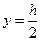 , то полагаем
, то полагаем 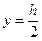 , x – любое число, например x=b/2. Подставляя в (19.11), найдем:
, x – любое число, например x=b/2. Подставляя в (19.11), найдем:
 .
.
Отсюда:  .
.
 .
.
Аналогично найдем точку границы ядра сечения для случая, когда нейтральная линия проходит вертикально (II-ая нейтральная линия) Тогда получим 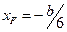 ,
, 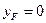 .
.
Точно так же определяются еще 2 точки. В результате получим ядро сечения, изображаемое на рисунке (19.16) в виде ромба.
Для двутавра, швеллера, круга ядра сечения имеют виды, приведенные на (рис.19.17).
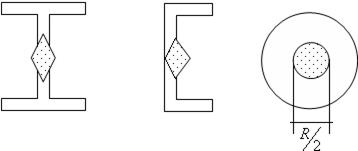
рис.19.17
Дата добавления: 2015-11-28; просмотров: 1302;
