Основное уравнение молекулярно-кинетической теории идеальных газов. Пусть в сосуде объемом V находится идеальный газ массой m, состоящий из N молекул массой m0, движущихся с одинаковыми скоростями v

Пусть в сосуде объемом V находится идеальный газ массой m, состоящий из N молекул массой m₀, движущихся с одинаковыми скоростями v. Концентрация молекул в газе n = N/V.

Если при соударениях со стенками за время Dt элементарной площадке DS стенки сосуда передается импульс Dp, то давление газа, оказываемое им на стенку сосуда:

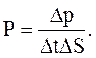
При каждом соударении молекула, движущаяся перпендикулярно стенке, передает ей импульс 2m₀v.

Рис.2.4

В среднем по направлению к стенке движется 1/6 часть всех молекул. Так, если рассмотреть три взаимно перпендикулярные оси (рис.2.4), то в среднем только 1/3 молекул движется вдоль одной из осей и только половина из них (1/6) - вдоль данного направления. Поэтому за время Dt площадки DS достигнут 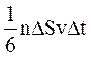молекул и передадут ей импульс .

Давление, оказываемое газом на стенку сосуда:

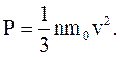(2.15)

Если газ в объеме V содержит N молекул, движущихся со скоростями v₁, v₂, ..., v_N, то целесообразно рассматривать среднюю квадратичную скорость, которая определяется как

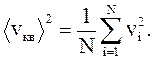(2.16)

Тогда выражение (2.15) примет вид:

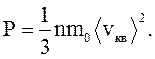(2.17)

Выражение (2.17) - основное уравнение молекулярно-кинетической теории идеальных газов.

Учитывая, что n=N/V и m=Nm₀, уравнение (2.17) можно представить и в других видах:

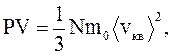(2.18)

(2.19)

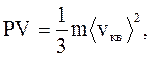(2.20)

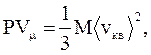(2.21)

где E – суммарная кинетическая энергия поступательного движения всех молекул газа, V_m - молярный объем, M – молярная масса.

Используя уравнение Менделеева-Клапейрона, получим

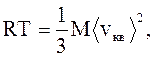
откуда (учитывая, что M = m₀N_A, k = R/N_A)

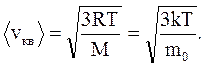(2.22)

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа

(2.23)

Отсюда следует, что áe₀ñ = 0 при T = 0 К, то есть при абсолютном нуле прекращается движение молекул газа.

Молекулярно-кинетическое толкование температуры: термодинамическая температура есть мера средней кинетической энергии поступательного движения молекул газа.