Работа объемного расширения газа
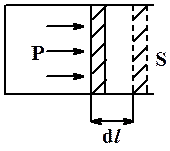 Рис.2.6. Давление газа на поршень
Рис.2.6. Давление газа на поршень
| Если находящийся под поршнем в цилиндрическом сосуде газ, расширяясь, передвигает поршень на расстояние dl (рис.2.6), то он производит над поршнем работу
dA = Fdl = PSdl = PdV, (2.38)
где S – площадь поршня.
Полная работа, совершаемая газом при изменении его объема от V1 до V2:
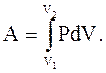 (2.39) (2.39)
|
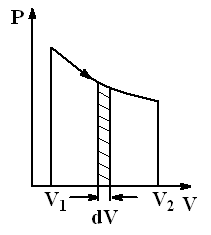 Рис.2.7. Равновесный процесс
Рис.2.7. Равновесный процесс
| Равновесные процессы – это процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесны, но в ряде случаев (достаточно медленные процессы) неравновесностью реальных процессов можно пренебречь. Равновесные процессы можно изображать графически в координатах (P,V) (рис.2.7). |
Так как работа 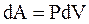 определяется площадью заштрихованной полоски, то полная работа – площадью под кривой между V1 и V2.
определяется площадью заштрихованной полоски, то полная работа – площадью под кривой между V1 и V2.
При неравновесных процессах значения параметров в разных частях системы различны и не существует (P,V)-точек, характеризующих состояние всей системы. Поэтому графическое изображение неравновесного процесса невозможно.
Теплоемкость
Удельная теплоемкость вещества c – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
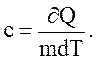 (2.40)
(2.40)
Единица удельной теплоемкости – Дж/(кг×К).
Молярная теплоемкость Cm - величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К:
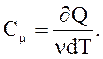 (2.41)
(2.41)
Единица удельной теплоемкости – Дж/(моль×К).
Связь между Cm и c:
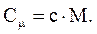
Различают теплоемкости (удельную и молярную) при постоянном объеме (сV и CmV) и при постоянном давлении (cP и CmP), если в процессе нагревания вещества его объем или давление поддерживаются постоянными.
1. Молярная теплоемкость при постоянном объеме
Из первого начала термодинамики 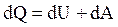 с учетом
с учетом 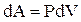 и
и 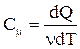 для 1 моль газа получим:
для 1 моль газа получим:
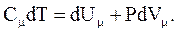
При 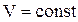 работа внешних сил
работа внешних сил 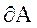 равна нулю и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии. Тогда
равна нулю и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии. Тогда
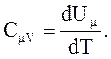
CmV равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К.
Поскольку 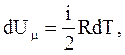 то
то
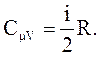 (2.42)
(2.42)
2. Молярная теплоемкость при постоянном давлении. Уравнение Майера
Если газ нагревается при 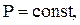 то
то

Слагаемое 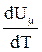 не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от P, ни от V, а определяется только T) и всегда равно CmV. Согласно уравнению Менделеева-Клапейрона
не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от P, ни от V, а определяется только T) и всегда равно CmV. Согласно уравнению Менделеева-Клапейрона 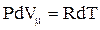 , тогда
, тогда
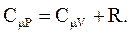 (2.43)
(2.43)
Выражение (2.43) – уравнение Майера.
СmP всегда больше CmV на величину универсальной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.
Тогда
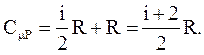 (2.44)
(2.44)
При рассмотрении термодинамических процессов важную роль играет величина
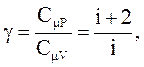 (2.45)
(2.45)
которая называется коэффициентом Пуассона.
Изопроцессы
1. Изохорный процесс (V = const)
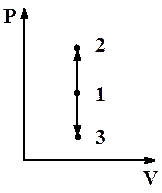 Рис.2.8. Изохорный процесс
Рис.2.8. Изохорный процесс
| Диаграмма этого процесса (рис.2.8) – изохора – в координатах (P,V) изображается прямой, параллельной оси ординат (ось P). Процесс 1-2 – изохорный нагрев, процесс 1-3 – изохорное охлаждение.
При изохорном процессе газ не совершает работу над внешними телами  и вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии и вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии 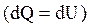 . Поскольку . Поскольку 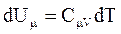 , то для произвольной массы газа , то для произвольной массы газа
|
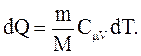 (2.46)
(2.46)
2. Изобарный процесс (P = const)
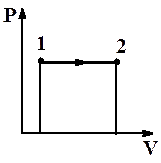 Рис.2.9. Изобарный процесс
Рис.2.9. Изобарный процесс
| Диаграмма этого процесса (рис.2.9) – изобара – в координатах (P,V) изображается прямой, параллельной оси абсцисс (ось V). При изобарном процессе работа газа при увеличении объема от V1 до V2 равна:
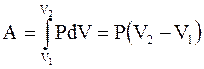 (2.47)
и определяется площадью прямоугольника под прямой 1-2. (2.47)
и определяется площадью прямоугольника под прямой 1-2.
|
Используя уравнение Менделеева-Клапейрона, получим:
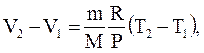
отсюда
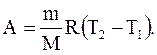 (2.48)
(2.48)
Физический смысл универсальной газовой постоянной: R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.
3. Изотермический процесс (T = const)
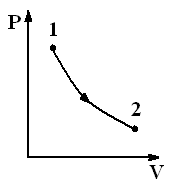 Рис.2.10. Изотермический процесс
Рис.2.10. Изотермический процесс
| Диаграмма этого процесса (рис.2.10) – изотерма – в координатах (P,V) представляет собой гиперболу. Изотермический процесс описывается законом Бойля-Мариотта (PV = const). Работа изотермического расширения газа |
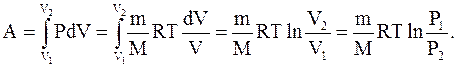 (2.49)
(2.49)
Так как при T = const внутренняя энергия идеального газа не изменяется, то из первого начала термодинамики следует, что 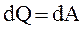 , то есть все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил.
, то есть все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил.
Поэтому для того, чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
4. Адиабатический процесс (dQ = 0)
Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (dQ = 0).
К адиабатическим процессам можно отнести все быстропротекающие процессы (теплообмен не успевает совершиться), например, распространение звука в среде, циклы расширения и сжатия в двигателях внутреннего сгорания, в холодильных установках и т.д.
Из первого начала термодинамики следует, что при адиабатическом процессе 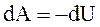 . Используя
. Используя 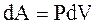 и
и 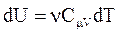 , получим:
, получим:
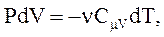 (2.50)
(2.50)
с другой стороны, из 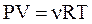 следует:
следует:
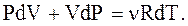 (2.51)
(2.51)
Разделив (2.51) на (2.50), получим:
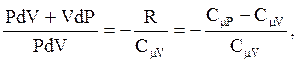
или
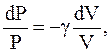 (2.52)
(2.52)
где 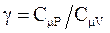 - коэффициент Пуассона.
- коэффициент Пуассона.
Проинтегрируем (2.52):
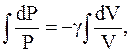
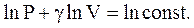
Потенциируя последнее выражение, получим уравнение Пуассона:
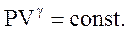 (2.53)
(2.53)
Используя уравнение Менделеева-Клапейрона, получим:
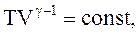 (2.54)
(2.54)
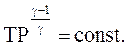 (2.55)
(2.55)
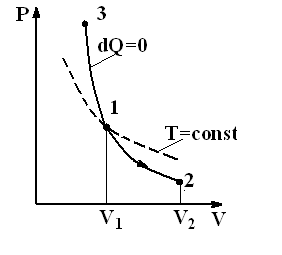 Рис.2.11. Адиабата и изотерма
Рис.2.11. Адиабата и изотерма
| Диаграмма адиабатического процесса (адиабата) в координатах (P,V) изображается гиперболой (рис.2.11). Адиабата ( 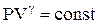 ) более крутая, чем изотерма ( ) более крутая, чем изотерма ( 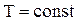 ). Это объясняется тем, что при адиабатическом сжатии (3-2) увеличение давления газа обусловлено не только уменьшением его объема, но и повышением температуры. ). Это объясняется тем, что при адиабатическом сжатии (3-2) увеличение давления газа обусловлено не только уменьшением его объема, но и повышением температуры.
|
В адиабатическом процессе  , поэтому
, поэтому 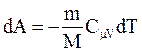 . Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газа
. Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газа
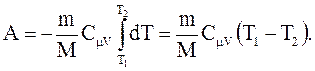 (2.56)
(2.56)
Откуда, используя уравнение Менделеева-Клапейрона, получаем:
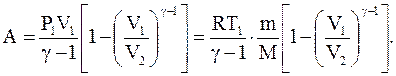
Работа адиабатического расширения 1-2 (рис.2.11, область под кривой 1-2) меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
Дата добавления: 2016-01-07; просмотров: 2996;
