Обратимый и необратимый процессы
Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении. Причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.
Реальные процессы необратимы, в них всегда происходит диссипация (потеря) энергии (из-за трения, теплопроводности и т.д.). Обратимые процессы – это физическая модель, идеализация реальных процессов.
Энтропия
Количество теплоты dQ, которое должно быть доставлено системе или отнято у нее при переходе из одного состояния в другое, не определяется однозначно начальным и конечным состояниями, но в значительной степени зависит от способа осуществления этого перехода.
Однако приведенное количество теплоты – отношение теплоты dQ к температуре T системы при бесконечно малых изменениях состояния системы – это функция состояния системы. В любом обратимом круговом процессе
 (2.58)
(2.58)
Следовательно, подынтегральное выражение есть полный дифференциал некоторой функции, которая определяется только начальным и конечным состояниями системы и не зависит от пути, которым система пришла в это состояние.
Энтропией S называется функция состояния системы, дифференциалом которой является dQ/T:
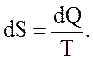 (2.59)
(2.59)
Изменение энтропии
В замкнутой системе для обратимых процессов  для необратимых процессов
для необратимых процессов 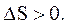
Энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов):
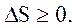 (2.60)
(2.60)
Поскольку dS и dQ имеют один и тот же знак, то по характеру изменения энтропии можно судить о направлении процесса теплообмена. При нагревании тела 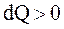 и его энтропия возрастает:
и его энтропия возрастает: 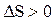 , при охлаждении
, при охлаждении 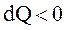 и энтропия тела убывает:
и энтропия тела убывает: 
Изоэнтропийным называется процесс, протекающий при постоянной энтропии (S = const).
В обратимом адиабатическом процессе 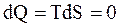 , так что
, так что 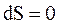 и S = const, поэтому адиабатический процесс является изоэнтропийным.
и S = const, поэтому адиабатический процесс является изоэнтропийным.
Рассмотрим для примера идеальный газ, который совершает равновесный переход из состояния 1 в состояние 2. Изменение его энтропии:
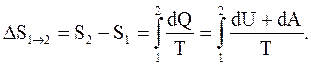
Используя соотношения:
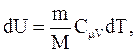
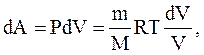


получим:
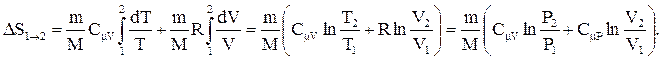
Таблица 2.3
Дата добавления: 2016-01-07; просмотров: 831;
