Энергия гармонических колебаний
Пусть гармонический осциллятор (ГО) колеблется по закону:
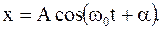
Полная энергия колебаний ГО равна:
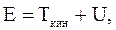 (1.68)
(1.68)
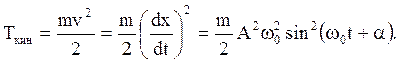 (1.69)
(1.69)
Найдем потенциальную энергию осциллятора, используя связь потенциальной энергии частицы с действующей на нее силой:
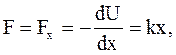
откуда
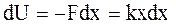 ,
,
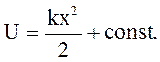 (1.70)
(1.70)
Выбрав постоянную так, чтобы потенциальная энергия в положении равновесия (x=0) обращалась в ноль, получим:
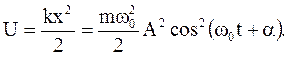 (1.71)
(1.71)
Тогда
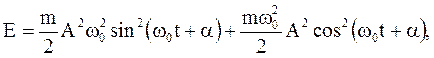
или
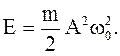 (1.72)
(1.72)
Поскольку гармонические колебания совершаются под действием упругой или квазиупругой силы, которая является консервативной, полная энергия гармонического колебания пропорциональна квадрату амплитуды и постоянна во все время колебания, как это следует из закона сохранения механической энергии. При этом кинетическая и потенциальная энергии непрерывно меняются с течением времени, переходя друг в друга.
Средние за период значения кинетической и потенциальной энергий одинаковы и равны:
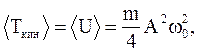 (1.73)
(1.73)
т.к. средние за период значения квадрата синуса и квадрата косинуса равны 1/2.
Физический маятник
Физическим маятником называют всякое абсолютно твердое тело, способное вращаться вокруг неподвижной оси, не проходящей через центр тяжести. Колебания физического маятника происходят под действием составляющей 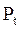 силы тяжести
силы тяжести 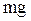 (рис.1.22):
(рис.1.22):
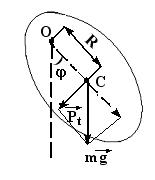 Рис.1.22. Физический маятник
Рис.1.22. Физический маятник
| 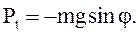 Знак «-» берется потому, что сила
Знак «-» берется потому, что сила 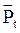 стремится вернуть маятник в положение равновесия. Сила стремится вернуть маятник в положение равновесия. Сила 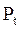 будет квазиупругой, т.е. пропорциональной смещению, только при малых углах отклонения будет квазиупругой, т.е. пропорциональной смещению, только при малых углах отклонения 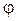 , когда , когда 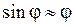 . Тогда . Тогда
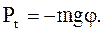 (1.74) (1.74)
|
Эта сила создает вращающий момент 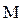 относительно оси вращения, проходящей через точку подвеса O перпендикулярно плоскости чертежа, равный:
относительно оси вращения, проходящей через точку подвеса O перпендикулярно плоскости чертежа, равный:
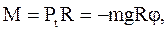 (1.75)
(1.75)
где R – расстояние от точки подвеса до центра тяжести C маятника.
Запишем уравнение вращательного движения относительно оси вращения:
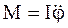 или
или 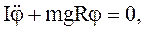 (1.76)
(1.76)
где I – момент инерции маятника относительно оси вращения, 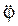 - угловое ускорение.
- угловое ускорение.
Разделив (1.76) на I, получим дифференциальное уравнение малых колебаний физического маятника:
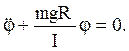 (1.77)
(1.77)
Из него следует, что частота колебаний физического маятника
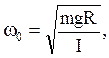 (1.78)
(1.78)
а период колебаний
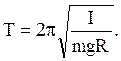 (1.79)
(1.79)
Приведенной длиной 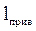 физического маятника называется длина такого математического маятника, который колеблется синхронно с физическим. Из условия синхронности
физического маятника называется длина такого математического маятника, который колеблется синхронно с физическим. Из условия синхронности 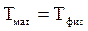 , где
, где 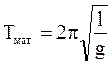 , найдем, что
, найдем, что 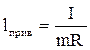 .
.
Дата добавления: 2016-01-07; просмотров: 680;
