Решение задачи с помощью Mathcad

Введите в рабочем листе поясняющий текст. Для этого поместите в позицию ввода курсор (визир – красный крестик) и выберите (щелчком мыши или с помощью клавиш) пункт Insert (Вставка) главного меню Mathcad. В появившемся падающем меню щелкните по пункту Text Region (Текстовая область) или в месте расположения курсора нажмите комбинацию клавиш Shift+" (двойная кавычка). В обоих случаях появится шаблон, указывающий начало ввода. По мере заполнения текстовая область будет автоматически увеличиваться. После этого курсор (маркер ввода) необходимо вывести за рамки текстовой области.

Задайте критерий оптимизации – целевую функцию. Для этого вначале поместите курсор (визир – красный крестик) в позицию ввода математического выражения. Затем с помощью соответствующих клавиш введите:

Y (X11, Х12, Х13, Х21, Х22, Х23, Х31, Х32, ХЗЗ)

Далее нажмите комбинацию клавиш Shift+: (двоеточие) для ввода знака присваивания :=. На месте правой метки расположите все выражение критерия оптимизации. Начальные приближения вводятся аналогично.

Для решения задачи используем блок функций Given... Minimize. С этой целью нужно:

• ввести, если необходимо, комментарии, воспользовавшись комбинацией клавиш Shift+";

• ввести ключевое слово Given;

• ввести систему ограничений. При этом используйте жирный знак равенства, вызываемый нажатием комбинации клавиш Ctrl+=;

• ввести граничные значения (рис. 3.3.1.3);

• ввести шаблон присваивания :=(двоеточие и знак равенства);

• ввести в левую метку шаблона вектор искомых переменных;

• ввести в правую метку шаблона имя функции Minimize с искомыми параметрами, например Minimize (Y,X11,X12,...), – рис. 3.3.1.4;

• вывести результаты расчета.

На рис. 3.3.1.3 показано начало процесса оптимизации распределения однородных ресурсов с помощью Mathcad. Это математическое описание конкретной транспортной задачи. Здесь представлены критерий оптимизации, начальные приближения и граничные значения. В описании двух первых пунктов использован знак присваивания := (двоеточие и равно). Он вводится щелчком левой кнопки мыши по второй кнопке в первой строке панели инструментов Evalu... (Вычисления), если панель выведена на рабочий лист. Знак присваивания может быть введен и нажатием комбинации клавиш Shift+: (двоеточие).

Следует обратить внимание на представление системы ограничений в Mathcad. При ее написании используется жирное равно, вызываемое щелчком по кнопке с жирным знаком равенства – второй в первом столбце панели инструментов Evalu...

На рис. 3.3.1.3 показано продолжение процесса оптимизации распределения однородных ресурсов с помощью Mathcad. Жирный знак равно (его еще называют булевым равенством) можно вывести нажатием комбинации клавиш Ctrl+= (равно).

Оптимальное распределение однородных ресурсов зафиксировано в векторе (XI1 Х12 Х13...). Из полученного решения видно: XI1– 4, Х12 = 2, Х13 – 8, Х21 – О, Х22=20, Х23=0, Х31=26, Х32=0, ХЗЗ=0. Это означает, что источник 1 должен профинансировать в первом периоде 4 единицы, во втором 2 и в третьем 8 единиц. Источник 2: в первом периоде 0 единиц, во втором 20 и в третьем 0 единиц. Источник 3: в первом периоде 26 единиц, во втором 2 и в третьем финансирование отсутствует. Первая цифра в переменной X определяет источник, а вторая – период финансирования. Такое распределение денежных средств из источников обеспечит минимальные суммарные затраты Y, которые составят 1402х10³ единиц.

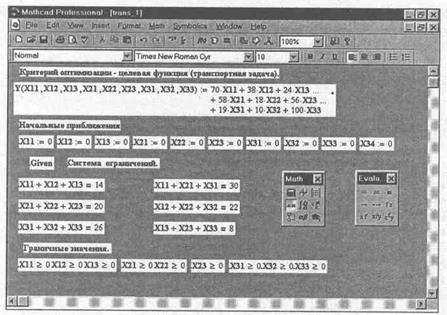
Рис 3.3.1.3 Оптимизация распределения однородных ресурсов

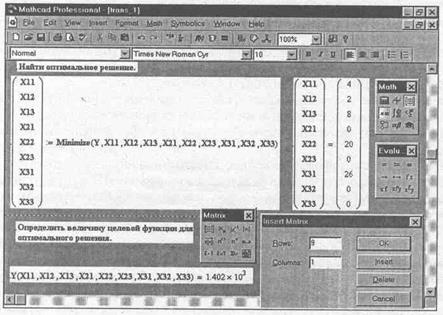
Рис 3.3.1.4 Продолжение оптимизации распределения однородных ресурсов

В рассмотренных задачах сумма объемов ресурсов поставщиков равна сумме объемов ресурсов потребителей. Однако в некоторых случаях такое равенство отсутствует.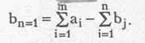

Если объем ресурсов всех поставщиков больше объема ресурсов всех потребителей, то вводят фиктивного потребителя В_п+1 с объемом потребления равным

Затраты на доставку единицы ресурса из пункта отправления до фиктивного пункта потребления должны быть одинаковыми и их принимают равными нулю: С1,n+1=С2,n+1= … =Сm,n+1=0.

Если объем ресурсов потребителей больше объема ресурсов поставщиков, то вводят фиктивного поставщика А_щ+1 с объемом поставки

Затраты на доставку единицы ресурса из фиктивного пункта отправления до каждого пункта потребления должны быть одинаковыми, и их принимают равными нулю: Сm+1,1= Сm+1,2= …=Сm+1,n=0.

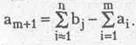
По преобразованным таблицам расчет выполняется так же, как и для сбалансированной транспортной задачи.