Решение задачи с использованием системы Mathcad. Введем в рабочий лист поясняющий текст

Введем в рабочий лист поясняющий текст. Для этого поместим курсор (визир – красный крестик) в позицию ввода текста. Затем выберем (щелчком мыши или с помощью клавиш) пункт Insert (Вставка) главного меню Mathcad. В появившемся падающем меню щелкнем по пункту Text Region (Текстовая область) или в месте расположения курсора нажмем комбинацию клавиш Shift+" (двойная кавычка). В обоих случаях появится шаблон, указывающий место и начало ввода. По мере заполнения текстовая область будет автоматически увеличиваться. По завершении ввода нужной информации выведем курсор за рамки области.

Далее зададим критерий оптимизации – целевую функцию. Для этого поместим курсор (визир – красный крестик) в позицию ввода математического выражения и начнем вводить имя критерия оптимизации с аргументами в скобках через запятые. Затем нажмем комбинацию клавиш Shift+: (двоеточие) для ввода знака присваивания := (двоеточие и равно). На месте правой метки расположим выражение критерия оптимизации. Аналогично вводятся начальные приближения.

Для решения задачи используем блок функций Given... Maximize. С этой целью необходимо:

• ввести, если нужно, комментарии, ввод которых начинается с нажатия комбинации клавиш Shift+";

• ввести ключевое слово Given;

• ввести систему ограничении, используя при этом жирный знак равенства' (Ctrl+= (равно)),

• ввести граничные значения (рис. 3.3.2.1),

• ввести вектор искомых переменных и знак присваивания;

• ввести в правую метку знака присваивания имя функции Maximize с искомыми параметрами, например Maximize (Y,X11,X12,...), – рис.3.3.2.1;

• вывести результаты расчета.

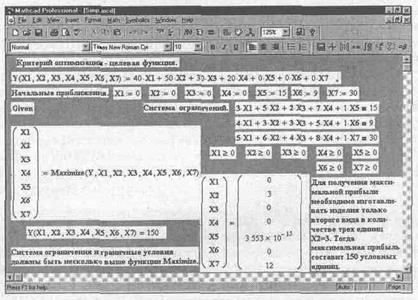
Рис 3.3.2.1 Оптимизация распределения неоднородных ресурсов

На рис. 3.3.2.1 показан процесс оптимизации распределения неоднородных ресурсов с помощью Mathcad

Оптимальное распределение неоднородных ресурсов зафиксировано в векторе (X_I Х₂ Х_З ) Из полученного решения видно X_I=О, Х₂=3, Х_З=О, Х₄=О, Х₅=- 3,553 X 10~¹⁵, Х_б=О, Х₇=12. Это означает, что изделия X_I, Х_З и Х₄ предприятие изготавливать не должно, ему выгодно производить только второе изделие в количестве трех единиц Цифра в переменной Х₂ определяет изделие, планируемое для изготовления Оптимальное распределение ресурсов обеспечит получение максимальной прибыли Y, которая составит 150 единиц

Тесты