Решение задачи традиционными методами. Алгоритм решения. Для решения задач данного типа разработано множество методов
Алгоритм решения. Для решения задач данного типа разработано множество методов. Рассмотрим самый распространенный – итерационный метод Эгервари-Куна. Студент должен в нем разобраться и уметь объяснить.
Алгоритм включает четыре основных этапа. Для поиска оптимального решения потребуется не более чем m–2 последовательно проводимых итераций.
1. Получение нулей в каждой строке и каждом столбце. Находим наименьший элемент в каждой строке исходной таблицы (табл. 1), вычитаем его из всех ее элементов и получаем новую таблицу (табл. 2). Аналогично производим действия для каждого столбца новой таблицы (табл. 2). Получаем табл. 3.
2. Проверка решения на оптимальность. Ищем строку с наименьшим числом нулей (в нашей задаче это строка 3), отмечаем звездочкой один из них и зачеркиваем все остальные нули строки и столбца, где есть нуль со звездочкой
Таблица 1. Здесь и ниже О(i) и К(i) – соответственно блоки и группы
| O(1) | O(2) | O(3) | O(4) | O(5) | |
| K(1) | |||||
| К(2) | |||||
| К(3) | |||||
| К(4) | |||||
| К(5) |
Таблица 2
| O(1) | O(2) | O(3) | O(4) | O(5) | |
| K(1) | |||||
| К(2) | |||||
| К(3) | |||||
| К(4) | |||||
| К(5) |
Аналогичные операции последовательно выполняем для всех строк. Если число нулей, отмеченных звездочкой, равно m, то решение является неоптимальным, в противном случае следует переходить к очередному шагу. В нашей задаче количество отмеченных звездочкой нулей не равно m, следовательно, решение неоптимально (табл. 4). Переходим к следующему этапу.
Таблица 3
| O(1) | O(2) | O(3) | O(4) | O(5) | |
| K(1) | |||||
| К(2) | |||||
| К(3) | |||||
| К(4) | |||||
| К(5) |
Таблица 4
| O(1) | O(2) | O(3) | O(4) | O(5) | |
| K(1) | | 0* | |||
| К(2) | 0* | ||||
| К(3) | 0* | ||||
| К(4) | | ||||
| К(5) | | 0* |
3. Поиск минимального набора строк и столбцов, содержащих нули. Необходимо отметить звездочкой:
а) все строки, не имеющие ни одного отмеченного звездочкой нуля (табл. 5, строка 4);
б) все столбцы, содержащие перечеркнутый нуль хотя бы в одной из отмеченных звездочкой строк (табл. 5, столбец 3);
в) все строки, содержащие отмеченные звездочкой нули хотя бы в одном из помеченных столбцов (табл. 5, строка 3), Далее поочередно повторяются действия б) и в) до тех пор, пока есть что отмечать.
После этого необходимо зачеркнуть каждую непомеченную строку, и каждый помеченный столбец. Цель этого этапа – провести минимальное количество горизонтальных и вертикальных прямых, пересекающих, по крайней мере, один раз все нули.
4. Перестановка некоторых нулей. В не вычеркнутых клетках (табл. 5, число 20) наименьший элемент вычитается из каждого элемента для непомеченных столбцов и прибавляется к каждому элементу непомеченной строки. Результаты расчета вносятся в новую таблицу (см. табл. 6).
Таблица 5
| O(1) | O(2) | O*(3) | O(4) | O(5) | |
| K(1) |  | 0* | |||
| К(2) | 0* | ||||
| К*(3) | 0* | ||||
| К*(4) | |||||
| К(5) | 0* |
Таблица 6
| O*(1) | O(2) | O*(3) | O*(4) | O*(5) | |
| K*(1) |  0* 0*
| ||||
| К*(2) | | 0* | |||
| К*(3) | | | |||
| К*(4) | 0* | | |||
| К(5) | 0* | |
Эта операция не изменяет оптимального решения. После нее выполняется новая итерация, цикл расчета начинается с этапа 2, и так до тех пор, пока не будет получено оптимальное решение. Поскольку число нулей, отмеченных звездочкой, не равно m, выполняется новый итерационный цикл, по завершении которого находится оптимальное решение (табл. 7).
Таблица 7
| O(1) | O(2) | O(3) | O(4) | O(5) | |
| K(1) | | 0* | |||
| К(2) | 0* | | | ||
| К(3) | | 0* | |||
| К(4) | | | 0* | ||
| К(5) | 0* |
Согласно ему распределение групп по блокам должно быть проведено так:
• первая группа разрабатывает пятый блок;
• вторая – первый;
• третья – третий;
• четвертая – четвертый;
• пятая – второй,
при этом себестоимость выполнения всех работ будет минимальной и составит Yмин=220 условных единиц
Решение задачи с использованием системы Mathcad (Пример)
Студент должен свободно владеть алгоритмом и с его помощью решить на ЭВМ задачу «своего варианта» (для своей «округленной» матрицы-задания).
Прежде всего, введем пояснительный текст в рабочем листе. Для этого установим курсор (визир – красный крестик) в место ввода. Затем выберем (щелчком мыши или с помощью клавиш) пункт Insert (Вставка) главного меню Mathcad. В появившемся падающем меню выберем пункт Text Region (Текстовая область) или в месте расположения курсора нажмем комбинацию клавиш Shift + “ (двойная кавычка). В обоих случаях появится шаблон, указывающий начало ввода текста. По мере заполнения текстовая область будет автоматически увеличиваться. По окончании этой операции выведем курсор (маркер ввода – красная вертикальная черточка) за рамки области.
Зададим критерий оптимизации – целевую функцию. Для этого установим курсор в место ввода математического выражения. Начнем с нажатия соответствующих клавиш. Сначала зададим имя критерия оптимизации Y с аргументами, записанными через запятые и заключенными в скобки. Далее нажмем комбинацию клавиш Shift+: (двоеточие) для получения знака присваивания :=. На месте правой метки расположим «свое» выражение критерия оптимизации, он равен раскрытому определителю исходной матрицы «своего» варианта задачи. Аналогично вводятся начальные приближения.
Для решения задачи используем блок функций Given ... Minimize С этой целью нужно:
• ввести, если необходимо, комментарии, нажав комбинацию клавиш Shift+“;
• ввести ключевое слово Given;
• ввести систему ограничений, такую же, как в примере. При этом используйте жирный знак равенства, вызвав его нажатием комбинации клавиш Ctrl+=;
• ввести граничные условия (рис. 3.2.1) (такие же, как в примере);
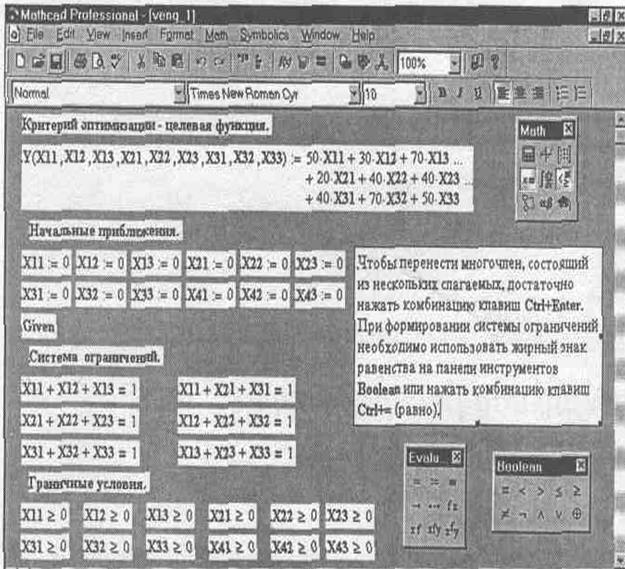
Рис 3.2.1 Формирование математической модели в Mathcad
• ввести шаблон присваивания := (двоеточие и знак равенства);
• ввести в левую метку шаблона вектор искомых переменных;
• ввести в правую метку шаблона имя функции Minimize с искомыми параметрами, например Minimize (Y,X11,X12,...);
• вывести результаты расчета.
На рис 3.2.2 представлены результаты решения задачи о назначении. Оптимальное распределение фиксируется в векторе (X11 Х12 Х21 ...) Из решения примера видно, что Х12=1, Х21=1 и ХЗЗ=1(Первая цифра в переменной X определяет группу, а вторая – блок). При таком распределении «групп по блокам» минимальная себестоимость Y в примере составляет 100 условных единиц.
Для другой исходной матрицы оптимальное распределение другое. Оно будет соответствовать полученной матрице.
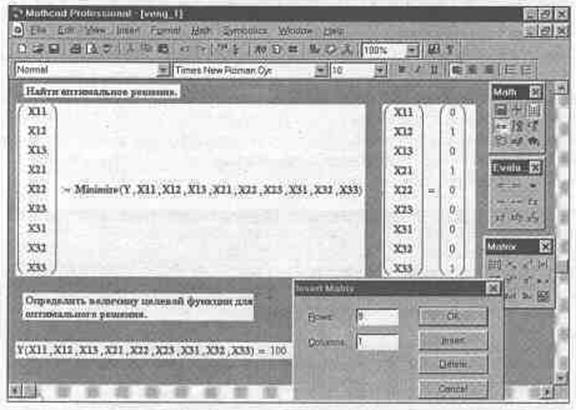
Рис 3.2.2. Поиск оптимальных распределений в Mathcad
Дата добавления: 2016-01-03; просмотров: 870;
