Количественных закономерностей

Введем переменные X(i,j), которые равны 1, если i-я группа разрабатывает j-й блок, и 0, если она не разрабатывает. Сформулируем ограничения:

1. Каждая группа может разрабатывать только один блок. Это ограничение можно записать в таком виде:

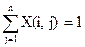, (i=1,2,...,m) (1)

2. Каждый блок может проектироваться только одной группой. Это ограничение можно записать так:

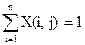, (j=1,2,...,m) (2)

Построение математической модели. В качестве критерия оптимизации примем условную себестоимость разработки всех блоков, образующих систему.

Обозначим через Y(i,j) себестоимость разработки j-го блока i-ой группой. Тогда критерий оптимизации Y – условная себестоимость разработки всех блоков запишется в таком виде:

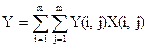(3)

Совокупность ограничений (1), (2) и целевой функции (3) образует математическую модель типичной экстремальной комбинаторной задачи. Ее решение представляет собой некоторую перестановку чисел, причем количество перестановок резко увеличивается с ростом m и равно M=m!. В рассматриваемом ниже примере m=5. В этом случае число перестановок составляет 5!=120. Студент должен разобраться в методе решения задачи на этом более общем примере и при выполнении «своего варианта» («m» определяется по согласованию с преподавателем, но не менее m=3), провести расчеты.

В научно-технической литературе задача относится к классу задач линейного программирования.