Изучение теплового излучения. определение степени черноты вольфрама лампы накаливания
3.1 Тепловое излучение и его характеристики
Тела, нагретые до достаточно высоких температур, способны излучать электромагнитные волны. Свечение тел, связанное с нагреванием получило название теплового излучения. Это излучение является самым распространенным в природе. Тепловое излучение может быть равновесным, т.е. может находиться в состоянии термодинамического равновесия с веществом в замкнутой (теплоизолированной) системе. Количественной спектральной характеристикой теплового излучения служит спектральная плотность энергетической светимости (излучательная способность):
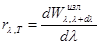 , (1)
, (1)
где 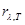 —спектральная плотность энергетической светимости;
—спектральная плотность энергетической светимости; 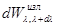 — энергия электромагнитного излучения, испускаемая за единицу времени с единицы площади поверхности тела в интервале длин волн от
— энергия электромагнитного излучения, испускаемая за единицу времени с единицы площади поверхности тела в интервале длин волн от 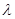 до
до 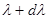 ;
;
Характеристикой полной мощности теплового излучения с единицы площади поверхности тела во всем интервале длин волн от 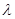 до
до 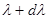 служит энергетическая светимость
служит энергетическая светимость 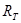 (интегральная энергетическая светимость):
(интегральная энергетическая светимость):

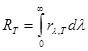 (2)
(2)
3.2. формула планка и законы Тепловое излучение черного тела
· закон стефана-больцмана
В 1900 г Планк выдвинул гипотезу, согласно которой атомные осцилляторы излучают энергию не непрерывно, а порциями—квантами. В соответствие с гипотезой Планка спектральная плотность энергетической светимости определяется следующей формулой:
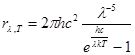 . (3)
. (3)
Из формулы Планка можно получить выражение для энергетической светимости. Подставим значение спектральной плотности энергетической светимости тела из формулы (3) в выражение (2):
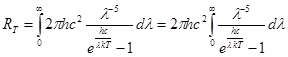 (4)
(4)
Для вычисления интеграла (4) введем новую переменную 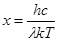 . Отсюда
. Отсюда 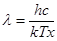 ;
; 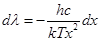 . Формула (4) при этом преобразуется к виду:
. Формула (4) при этом преобразуется к виду:
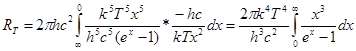 . (5)
. (5)
Так как 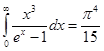 , то выражение (5) для энергетической светимости будет иметь следующий вид:
, то выражение (5) для энергетической светимости будет иметь следующий вид:
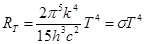 . (6)
. (6)
Соотношение (6) представляет собой закон Стефана-Больцмана, где постоянная Стефана-Больцмана 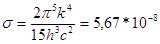 Вт/(м2К4).
Вт/(м2К4).
Отсюда вытекает определение закона Стефана-Больцмана:
Энергетическая светимость абсолютно черного тела прямопропорциональна четвертой степени абсолютной температуры.
В теории теплового излучения наряду с моделью черного тела часто пользуются понятием серого тела. Тело называется серым, если его коэффициент поглощения одинаков для всех длин волн и зависит только от температуры и состояния поверхности. Для серого тела закон Стефана-Больцмана имеет вид:
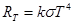 , (7)
, (7)
где 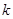 — коэффициент излучения теплового излучателя (коэффициент черноты).
— коэффициент излучения теплового излучателя (коэффициент черноты).
· первый закон вина (закон смещения Вина)
Исследуем соотношение (3) на экстремум. Для этого определим первую производную от спектральной плотности по длине волны и приравняем ее к нулю.
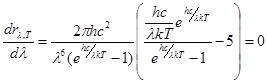 . (8)
. (8)
Введем переменную 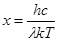 . Тогда из уравнения (8) получим:
. Тогда из уравнения (8) получим:
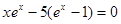 . (9)
. (9)
Трансцендентное уравнение (9) в общем случае решается методом последовательных приближений. Так как для реальных температур 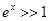 , то можно найти более простое решение уравнения (9). Действительно, при этом условии соотношение (9) упрощается и принимает вид:
, то можно найти более простое решение уравнения (9). Действительно, при этом условии соотношение (9) упрощается и принимает вид:
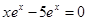 ,
,
которое имеет решение при 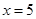 . Следовательно
. Следовательно
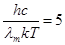 .
.
Отсюда
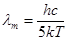 .
.
Более точное решение уравнения (9) методом последовательных приближений приводит к следующей зависимости:
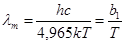 , (10)
, (10)
где 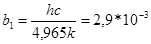 мК.
мК.
Из соотношения (10) вытекает определение первого закона Вина (закона смещения Вина).
Длина волны 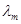 , соответствующая максимальной спектральной плотности энергетической светимости обратнопропорциональна температуре тела.
, соответствующая максимальной спектральной плотности энергетической светимости обратнопропорциональна температуре тела.
Величина 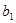 получила название постоянной закона смещения Вина.
получила название постоянной закона смещения Вина.
· второй закон вина
Подставим значение 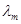 из уравнения (10) в выражение спектральной плотности энергетической светимости (3). Тогда получим максимальную спектральную плотность:
из уравнения (10) в выражение спектральной плотности энергетической светимости (3). Тогда получим максимальную спектральную плотность:
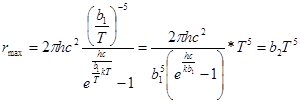 , (11)
, (11)
где 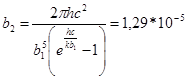 Вт/м2К5.
Вт/м2К5.
Из соотношения (11) вытекает определение второго закона Вина.
Максимальная спектральная плотность энергетической светимости абсолютно черного тела прямопропорциональна пятой степени абсолютной температуры.
Величина 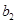 получила название постоянной второго закона Вина.
получила название постоянной второго закона Вина.
На рисунке 1 представлена зависимость спектральной плотности энергетической светимости от длины волны для некоторого тела при двух различных температурах. С повышением температуры площадь под кривыми спектральной плотности должна увеличиваться пропорционально четвертой степени температуры в соответствии с законом Стефана-Больцмана, длина волны, соответствующая максимальной спектральной плотности уменьшаться обратнопропорционально температуре согласно закону смещения Вина и максимальное значение спектральной плотности увеличиваться прямопропорционально пятой степени абсолютной температуры в соответствии со вторым законом Вина.
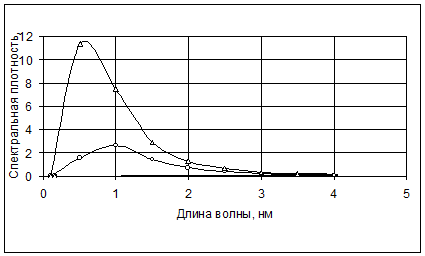
Рисунок 1
4. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ. ОПИСАНИЕ УСТАНОВКИ
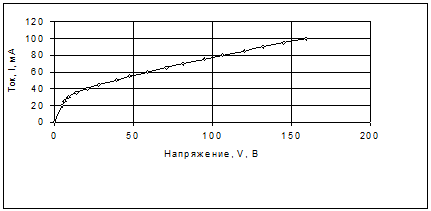
В данной работе в качестве излучающего тела используется нить накала электрических ламп различной мощности (25, 60, 75 и 100 Вт). Для определения температуры нити накаливания электрических лампочек снимается вольтамперная характеристика, по которой определяется величина статического сопротивления ( 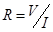 ) нити накаливания и рассчитывается ее температура. На рисунке 2 представлена типичная вольтамперная характеристика лампы накаливания. Видно, что при малых значениях тока ток линейно зависит от приложенного напряжения и соответствующая прямая проходит через начало координат. При дальнейшем увеличении тока нить накала разогревается, сопротивление лампы увеличивается и наблюдается отклонение вольтамперной характеристики от линейной зависимости, проходящей через начало координат. Для поддержания тока при большем сопротивлении требуется большее напряжение. Дифференциальное сопротивление лампы
) нити накаливания и рассчитывается ее температура. На рисунке 2 представлена типичная вольтамперная характеристика лампы накаливания. Видно, что при малых значениях тока ток линейно зависит от приложенного напряжения и соответствующая прямая проходит через начало координат. При дальнейшем увеличении тока нить накала разогревается, сопротивление лампы увеличивается и наблюдается отклонение вольтамперной характеристики от линейной зависимости, проходящей через начало координат. Для поддержания тока при большем сопротивлении требуется большее напряжение. Дифференциальное сопротивление лампы 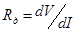 монотонно уменьшается, а затем принимает почти постоянное значение и вольтамперная характеристика в целом носит нелинейный характер. Считая, что потребляемая электрической лампой мощность
монотонно уменьшается, а затем принимает почти постоянное значение и вольтамперная характеристика в целом носит нелинейный характер. Считая, что потребляемая электрической лампой мощность 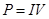 отводится излучением, можно определить коэффициент черноты
отводится излучением, можно определить коэффициент черноты 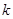 нити накаливания лампы или оценить постоянную Стефана-Больцмана по формуле:
нити накаливания лампы или оценить постоянную Стефана-Больцмана по формуле:
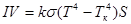 , (12)
, (12)
где 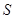 - площадь нити накаливания лампы;
- площадь нити накаливания лампы; 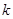 - степень черноты;
- степень черноты;  - постоянная Стефана-Больцмана.
- постоянная Стефана-Больцмана.
Из формулы (12) можно определить коэффициент черноты нити накаливания электрической лампы.
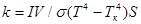 . (13)
. (13)
Рисунок 2
На рисунке 3 представлена электрическая схема установки для снятия вольтамперной характеристики лампы, определения сопротивления нити, её температуры и изучения законов теплового излучения. Ключи К1 и К2 предназначены для подключения электроизмерительных приборов с необходимыми пределами измерения тока и напряжения.
Переменное сопротивление 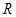 подключается в цепь переменного тока с напряжением сети 220В по потенциометрической схеме, обеспечивающей плавное изменение напряжения от 0 до 220 В.
подключается в цепь переменного тока с напряжением сети 220В по потенциометрической схеме, обеспечивающей плавное изменение напряжения от 0 до 220 В.
Определение температуры нити накаливания основано на известной зависимости сопротивления металлов от температуры:
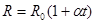 , (14)
, (14)
где 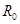 - сопротивление нити накаливания при 00С;
- сопротивление нити накаливания при 00С; 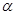 - температурный коэффициент сопротивления вольфрама,
- температурный коэффициент сопротивления вольфрама, 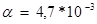 1/град.
1/град.
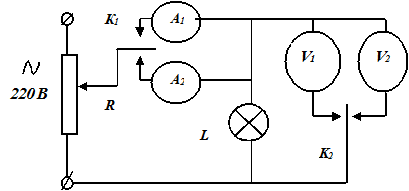
Рисунок 3
Запишем выражение (14) для комнатной температуры.
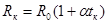 . (15)
. (15)
Разделив почленно выражение (14) на (15), получим:
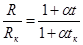 . (16)
. (16)
Отсюда определим температуру нити накаливания:
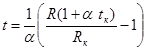 . (17)
. (17)
Таким образом, зная статическое сопротивление 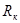 нити накаливания в отсутствии тока при комнатной температуре
нити накаливания в отсутствии тока при комнатной температуре 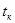 и сопротивление
и сопротивление 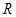 нити при протекании тока можно определить температуру нити. При выполнении работы сопротивление
нити при протекании тока можно определить температуру нити. При выполнении работы сопротивление 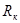 при комнатной температуре измеряется цифровым электроизмерительным прибором (тестером), а статическое сопротивление
при комнатной температуре измеряется цифровым электроизмерительным прибором (тестером), а статическое сопротивление 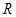 нити накаливания рассчитывается по закону Ома
нити накаливания рассчитывается по закону Ома
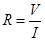 . (18)
. (18)
6. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Выкрутите лампу накаливания из патрона и с помощью цифрового электроизмерительного прибора определите сопротивление нити испытываемой электрической лампы при комнатной температуре. Результаты измерений запишите в таблицу 1.
2. Вверните лампу в патрон, снимите вольтамперную характеристику лампы (зависимость силы тока от напряжения). Силу тока измеряйте через каждые 5 мА после непродолжительной выдержки в течение 2-5 мин.. Результаты измерений запишите в таблицу 1.
3. Рассчитайте по формуле (18) и (17) сопротивление и температуру нити в 0С и К.
4. Рассчитайте по формуле (13) коэффициент черноты нити накаливания. Результаты расчет запишите в таблице 1.
Экспериментальные данные для расчета коэффициента черноты
Таблица 1
| № | I, | V, | P, | R, | t, | T, | S, | k |
| мА | В | Вт | Ом | 0С | К | м2 | ||
5. По данным таблицы 1 постройте вольтамперную характеристику лампы, зависимости сопротивления и коэффициента черноты от температуры и мощности.
6. Определите для исследуемого температурного интервала среднее значение коэффициента черноты, величину абсолютной и относительной погрешности. Окончательные результаты представьте в виде: 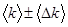 ,
, 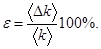 Данные расчетов запишите в таблицу2.
Данные расчетов запишите в таблицу2.
7. Повторите измерения для других ламп накаливания с мощностью 40, 60, и 75 Вт.
8. Сделайте краткие выводы по работе.
Результаты расчета коэффициента черноты и определение огрешности измерений.
Таблица 2
| № | k | <k> | Dki | Dki2 | DS | <Dk> | e, % |
7.
| <== предыдущая лекция | | | следующая лекция ==> |
| ИЗУЧЕНИЕ ТЕПЛОВОГО ИЗЛУЧЕНИЯ ТВЕРДЫХ ТЕЛ | | | ИЗУЧЕНИЕ ЯВЛЕНИЯ ИНТЕРФЕРЕНЦИИ СВЕТА В ОПЫТЕ ЮНГА И С ПОМОЩЬЮ БИПРИЗМЫ ФРЕНЕЛЯ. |
Дата добавления: 2016-01-03; просмотров: 3358;
