ИЗУЧЕНИЕ ЯВЛЕНИЯ ИНТЕРФЕРЕНЦИИ СВЕТА В ОПЫТЕ ЮНГА И С ПОМОЩЬЮ БИПРИЗМЫ ФРЕНЕЛЯ.
Когерентные или частично когерентные пучки света можно получить двумя способами: делением фронта световой волны и делением светового пучка по амплитуде. В настоящей работе рассматриваются две интерференционные схемы относящиеся к первому способу.
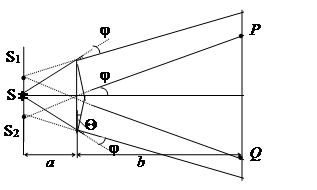
Опыт Юнга. Согласно опыта Юнга источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие щели S1 и S2, освещаемые, таким образом, различными участками одного и того же волнового фронта. Световые пучки, проходящие через малые отверстия S1 и S2 расширяются в результате дифракции и частично перекрываются, создавая интерференционную картину (рисунок 1).
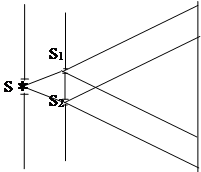 Рисунок 1
Рисунок 1
|
Щели S1 и S2 (рис.2) находятся на расстоянии d друг от друга и являются когерентными источниками света. Интерференция наблюдается в произвольной точке А экрана, расположенного параллельно обеим щелям на расстоянии l от них, причем l>>d.
|
Начало отсчета выбрано в точке О, симметричной относительно щелей. Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода = s2 - s1. Из рис.2 следует:
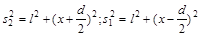
откуда
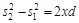
или
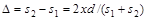 .
.
Учитывая, что l>>d, и s1+s1~2l получаем:
D = xd/l. (1)
Тогда максимумы интенсивности интерференции света будут наблюдаться при
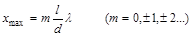 , (2)
, (2)
а минимумы соответствовать условию
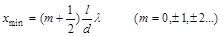 . (3)
. (3)
Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно
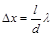 ( 4 )
( 4 )
Dx не зависит от порядка интерференции (величины m) и является постоянной величиной при заданных l, d иD. Используя полученное выражение для ширины интерференционной полосы, при известных величинах Dx, l, d можно рассчитать длину световой волны:
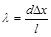 . (5)
. (5)
|

|
Бипризма Френеля. Интерференционная картина получаемая с помощью бипризмы Френеля возникает в результате преломления света в бипризме, при наложении когерентных волн от мнимых источников S1 и S2 (рисунок 3). Параллельно общей грани бипризмы, на расстоянии а от нее, располагается источник света S. Можно
Рисунок 3
показать, что в случае, когда преломляющий луч D мал и углы падения лучей на грань призмы не очень велики, все лучи отклоняются призмой практически на одинаковый угол, равный
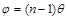 ( 6 )
( 6 )
(n - показатель преломления призмы). Угол падения лучей на бипризму невелик, поэтому все лучи отклоняются каждой из половин бипризмы на одинаковый угол. В результате образуются две когерентные цилиндрические волны, исходящие из мнимых источников S1 и S2, лежащих в одной плоскости с источником света S.
В данном эксперименте расстояние между источниками равно
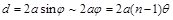 , ( 7 )
, ( 7 )
а расстояние от источников до экрана
l = a + b.
Тогда, используя формулу (4), найдем ширину интерференционной полосы следующим образом:
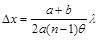 . ( 8 )
. ( 8 )
Область перекрытия волн PQ в таком эксперименте имеет протяженность
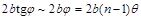 ( 9 )
( 9 )
и максимальное число наблюдаемых интерференционных полос можно определить по следующей формуле:
 . (10)
. (10)
4. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
1. Оптическая скамья.
2. Лазер.
3. Линза
4. Щели Юнга.
5. Бипризма Френеля.
6. Экран для наблюдения.
5. РАБОТА С ЛАЗЕРОМ
Во время работы с лазером необходимо помнить, что попадание в глаза прямого лазерного излучения опасно для зрения. Категорически запрещается смотреть на прямой лазерный луч! Включать лазер можно только под контролем преподавателя или лаборанта.
6. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1
Определение длины волны в опыте Юнга.
1.1 Собрать оптическую схему, представленную на рис.4а. Включить лазер. Ввести в лазерный пучок собирающую линзу. Установить щели Юнга (рис.4б) в лазерный пучок и получить интерференционную картину на экране.
|
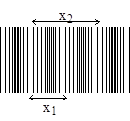
|
| |
| |||||
 | |||||
| |||||
1. Лазер
2. Собирающая линза
3. Щели Юнга
4. Экран
1.2 Измерить линейкой расстояние l между щелями и экраном.
1.3 Измерить ширину интерференционной полосы x1 (расстояние между соседними максимумами). Повторив измерения несколько раз найти среднее значение ширины полосы 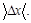
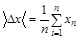
1.4 Используя выражение для ширины интерференционных полос (4), рассчитать длину волны лазерного излучения
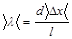
Данные занести в таблицу 1.
Таблица 1
| l ,м | 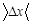 ,м ,м
| d, м | l, м |
| 0,1. 10-3 |
1.5 Вычислить относительную погрешность длины волны 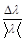
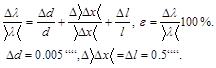
Найти абсолютную погрешность 
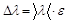 . Результат записать в виде
. Результат записать в виде 
Найденные значения 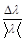 и
и 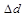 будут использоваться в упражнении 2.
будут использоваться в упражнении 2.
Упражнение 2
Определение расстояния между мнимыми источниками света в опыте с бипризмой Френеля.
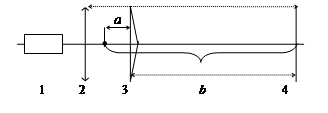
2.1 Собрать оптическую схему, изображенную на рисунке 5. Включить лазер. Ввести в лазерный пучок собирающую линзу. Установить бипризму Френеля в лазерный пучок и разместить экран для наблюдения на максимально возможном расстоянии, получить интерференционную картину.
 |
|
 |

Рисунок 5
1. Лазер
2. Собирающая линза
3. Бипризма Френеля
4. Экран для наблюдения
2.2 Измерить линейкой расстояние l между плоскостью основания призмы и экраном, а также расстояние L от экрана до линзы (рисунок 5).
2.3. Измерить расстояния xn между несколькими интерференционными полосами и найти среднее значение ширины полосы 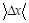 (например, для пяти полос
(например, для пяти полос 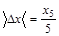 рисунок 5):
рисунок 5):
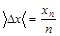
2.4 Определить расстояние между мнимыми источниками света, используя выражение для ширины интерференционной полосы (4)
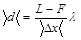
Данные занести в таблицу 2.
Таблица 2
| l, м | l ,м | L, м | 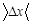 ,м ,м
| <d>, м | F, м | 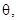 рад рад
| n |
| 5.10-2 | 6.10-3 |
2.5 Вычислить относительную погрешность по формуле

Найти абсолютную погрешность по формуле 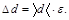
Окончательный результат записать в виде 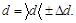
Упражнение 3
Определение показателя преломления материала бипризмы Френеля.
3.1 По данным таблицы 2, используя выражение (8) рассчитать величину показателя преломления n бипризмы
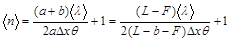
Полученный результат занести в таблицу 2.
3.2 Рассчитать относительную и абсолютную погрешность измерения по следующим формулам, учитывая, что:
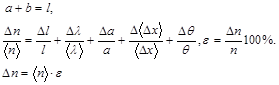
3.3 Окончательный результат записать в виде 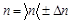 .
.
3.4 Сделать выводы по работе.
| <== предыдущая лекция | | | следующая лекция ==> |
| Изучение теплового излучения. определение степени черноты вольфрама лампы накаливания | | | ИЗУЧЕНИЕ ВРАЩЕНИЯ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ СВЕТА. ЗАКОН МАЛЮСА |
Дата добавления: 2016-01-03; просмотров: 2506;


 Рисунок 2
Рисунок 2