Пример расчета (задача № 22)

В рассмотрим эллиптическую пластинку, жестко заделанную по контуру и нагруженную равномерно распределенной нагрузкой ин­тенсивностью q (рис. 11.4). При a = 1,3 м, b = 1,0 м, h = 0,18 м, q = 300 кН/м², g = 1/6, Е = 2×10⁸ кН/м², требуется:

1. Определить прогиб пластины в ее середине;

2. Построить эпюры изгибающих моментов и поперечных сил в пласти­не по направлениям глав­ных диаметров контура;

3. В точке С с коор­динатами (а/2, b/2) опре­делить изгибающие мо­менты М_x , M_y и крутя­щий момент M_xy .

Решение

Выберем начало коор­динат в центре пластинки и запишем уравнение контура (в нашем случае - уравнение эллипса):

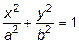. (11.10)

При жесткой заделке во всех контурных точках (11.10) должны выполняться следующие граничные условия: ,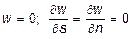

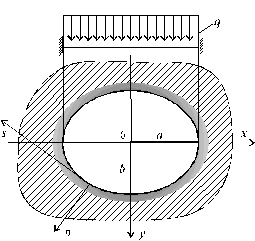Рис. 11.4

где n и s - нормаль и касательная к контуру пластины, соответ­ственно. Нетрудно убедиться, что этим условиям удовлетворяет функция

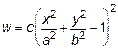, (11.11)

где с - прогиб в центре пластинки.

Действительно в результате дифференцирования функции w по n получим:

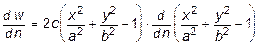. (11.12)

Но поскольку, на основании (11.10) в контурных точках

,

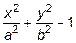то выражения (11.11) и (11.12) на контуре обращаются в нуль. Ана­логично можно доказать, что условие 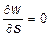также выполняется на контуре.

Проверим, удовлетворяет ли выбранная функция w основному дифференциальному уравнению (11.9). Вычислим частные произ­водные

.

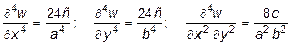и подставим их в (11.9). Результатом будет выражение

.

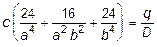Очевидно, что оно справедливо в случае, если q = const, а прогиб в центре будет равен

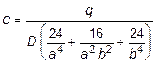. (11.13)

Выражения изгибающих моментов M_x и M_y и крутящего мо­мента М_xy в произвольной точке пластинки в соответствии с (11.7) будут иметь вид:

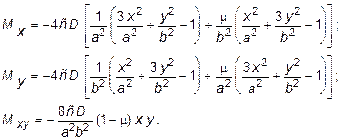(11.14)

Моменты на концах малой полуоси (x = 0, y = ±b) согласно (11.14) будут равны:

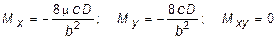(11.15)

В точках, расположенных на концах большой полуоси (x = ±a, y = 0) моменты равны:

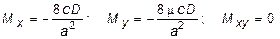(11.16)

И, наконец, в центре пластины (x = y = 0) моменты равны:

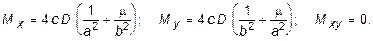(11.17)

В данном случае имеем:

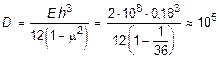кН×м;

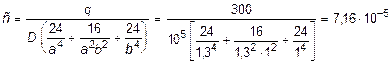м.

Для точки C(0,5a; 0,5b) выражения 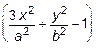и 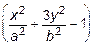равны нулю, следовательно: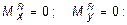

.

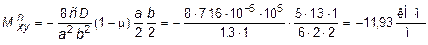Для построения эпюр M_x и M_y достаточно найти их значения в трех точках по осям эллипса, так как вдоль них эти функции имеют параболический характер изменения, для этого воспользуемся фор­мулами (11.15) ¸ (11.17):

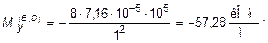
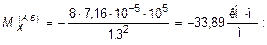
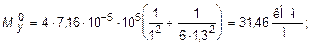
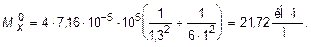
При построении эпюр следует помнить, что 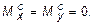Ве­личины поперечных сил вдоль координатных осей могут быть вы­числены по формуле (11.8)

.

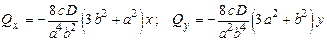В данном случае 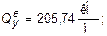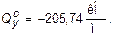Аналогично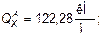

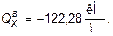
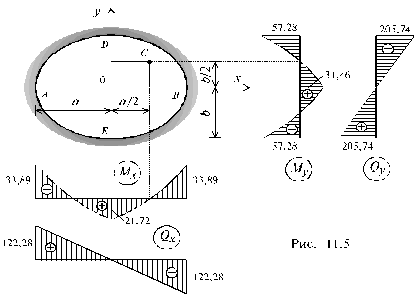
По данным вычислений построены эпюры M_x , M_y , Q_x и Q_y (рис. 11.5). Поскольку из условий равновесия пластинки следует, что

,

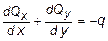то в данном случае легко сделать проверку графически. Действи­тельно,

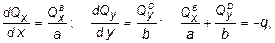
где 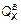= -122,28 кН/м (с эпюры Q_x ), 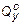= -205,74 кН/м (с эпюры Q_y ), q = 300,0 кН/м (по условию), тогда:

.

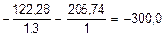Таким образом, задача решена правильно.