Теория тонких пластин

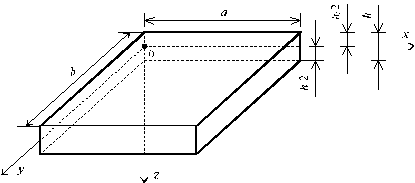
Под оболочкой понимается тело, одно из измерений которого, называемое толщиной, значительно меньше двух других. Геометри­ческое место точек, равностоящих от обеих поверхностей оболочки, носит название срединной поверхности. Если срединная по­верхность оболочки является плоскостью, то такую оболочку назы­вают пластиной (рис. 11.1.).

Рис. 11.1

Предполагаем, что на поверхности пластины действует распределенная нагрузка интен­сивностью q = q (x, y). Для вывода диф-ференциального уравнения изогнутой поверх­ности пластинки выделим из ее состава бесконечно малый элемент с раз­мерами dx, dy, h, где h - толщина пластины. Выделенный элемент с указанными внутрен­ними усилиями изображен на рис. 11.2. Определим внутренние усилия в пластине следующим образом.

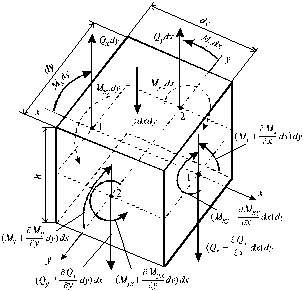Рис. 11.2

Для этого отметим характерную для пластин особенность обозначения изгибающих моментов отличны от тех, что приняты в балках, а именно: М_x - изгибающий момент на площадке с нормалью парал­лельной оси x; аналогично, М_y - изгибающий момент на площадке с нормалью параллельной оси y; М_xy - крутящий момент относи­тельно оси x, действующий в плоскости параллельной оси y; М_yx - крутящий момент относительно оси y, действующий в плоскости параллельной оси x (см. рис. 10.2). Различие между Q_x и Q_y состоит в том, что интегрирование ведется по площадке с нормалью параллельной оси x, в первом случае, и по площадке с нормалью параллельной оси y во втором. С учетом изложенного выражения усилий записываются в следующем виде:

;

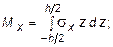
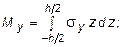
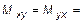
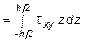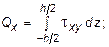
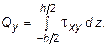
Проецируя все силы, приложен­ные к элементу пластинки на вертикальную ось z, из условия равновесия получим:

,

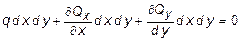откуда

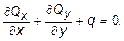(11.1)

Далее, составляя условия равновесия в форме суммы моментов относительно координатных осей x и y, и пренебрегая малыми ве­личинами второго порядка, получим:

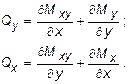(11.2)

Подставляя выражения Q_x и Q_y из (11.2) в (11.1), получим:

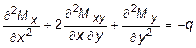. (11.3)

Очевидно, что для определения трех величин М_x , М_y и М_xy од­ного уравнения (11.3) недостаточно. Для решения задачи необхо­димо выразить моменты через прогибы пластинки. С этой целью для тонких пластинок вводится следующие допущения:

1. Отрезок нормали к срединной поверхности при изгибе ос­тается прямым и перпендикулярным к срединной поверхности. Это допущение носит название гипотезы прямых нормалей.

2. Величины s_z и e_z пренебрежимо малы и в расчете не учиты­ваются.

Поскольку, мы предположили, что e_z = 0, то

e_z = ,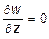

следовательно, прогиб пластины w не зависит от координаты z, то есть w = w (x, y).

Пользуясь сделанными предположениями, выразим перемеще­ние точек пластины вдоль осей x и y, соответственно, u и v через их прогиб w.

Согласно рис. 11.3. можно записать:

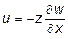. (11.4)

Рис. 11.3

Нормаль к срединной поверхности пластинки (C - C) согласно гипотезе прямых нормалей и в де­формируемом состоянии пластинки 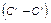оста­ется перпендикулярной к искривленной поверхнос­ти. Аналогичным образом получим:

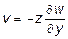. (11.5)

Закон Гука в данном случае преобразуется к виду:

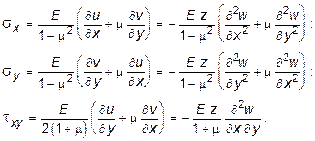(11.6)

Выражения для изгибающих моментов с учетом (11.6) принима­ют вид:

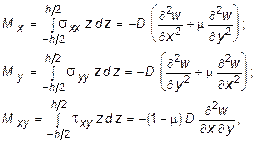(11.7)

где 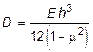- цилиндрическая жесткость пластины.

Пользуясь соотношениями (11.2) и (11.7), выражения для попе­речных сил можно записать следующим образом:

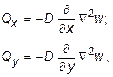(11.8)

где 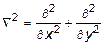- оператор Лапласа.

Согласно (11.7) величины моментов определяются через один искомый параметр - прогиб пластины w (x, y). Следовательно, под­ставляя выражение (11.7) в (11.3), окончательно получим

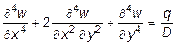. (11.9)

Выражение (11.9) - известное дифференциальное уравнение изогнутой срединной поверхности пластины, полученное Софи Жермен и опубликованное Лагранжом в 1811 году.