Прочность толстостенной цилиндрической оболочки при действии внутреннего и внешнего давлений
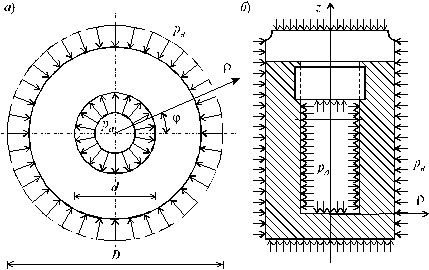
Рассмотрим однородное тело цилиндрической формы в цилиндрической системе координат r, j, z (рис. 11.6, а) при действии внутреннего pa и внешнего давления pb , которые являются осесимметричными нагрузками и вдоль оси z являются постоянными величинами (рис. 11.6, б).
Радиальное перемещение произвольно взятой точки обозначим через u. Величина u в данном случае является функцией только от текущего радиуса r.
|
Рис. 11.6
Обозначим er и ej относительное удлинение в цилиндре в радиальном и окружном направлении и выразим их через перемещение u. Рассмотрим элементарный отрезок АВ = dr, выделенный в радиальном направлении до и после нагружения цилиндра (рис. 11.7, а). Для определения ej достаточно рассмотрения рис. 11.7, б.

|
Рис. 11.7
С учетом принятых обозначений и формы деформирования цилиндра получим:
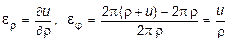 . (11.18)
. (11.18)
Для изучения напряженного состояния выделим из цилиндра элемент в форме криволинейного шестигранника (рис. 11.8). В осевых сечениях цилиндра из условий симметрии касательные напряжения отсутствуют и сохраняются только нормальные окружные напряжения sj .

|
Рис. 11.8
Поскольку в поперечных и радиальных сечениях касательные напряжения также отсутствуют, следовательно, площадки в поперечном, радиальном и тангенциальном направлениях являются главными площадками, а напряжения sz , sr , sj являются главными напряжениями.
Проецируя силы, действующие на выделенный элемент (рис. 11.8), на радиальное направление, получим следующее условие равновесия:
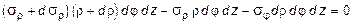 ,
,
откуда
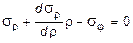 . (11.19)
. (11.19)
Остальные уравнения равновесия для элемента выполняются тождественно.
Закон Гука в данном случае принимает вид:
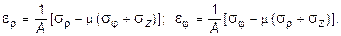 (11.20)
(11.20)
Деформация по направлению z отсутствует, из предположения, что цилиндр бесконечно длинный, т.е. ez = 0
Выражение напряжений в осевом направлении определяется самостоятельно, если учесть, что в поперечных сечениях цилиндра с площадью 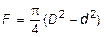 действует продольная сила:
действует продольная сила:
Nz = - 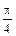 (pв D 2 - pa d 2).
(pв D 2 - pa d 2).
Следовательно,
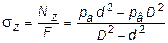 . (11.21)
. (11.21)
Из (11.20) с учетом (11.18) выражения для напряжений sj и sr принимают вид:
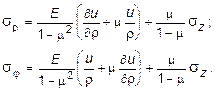 (11.22)
(11.22)
Тогда уравнение равновесия (11.19) с учетом (11.22) примет окончательный вид:
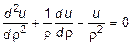 . (11.23)
. (11.23)
Решение (11.23) записывается в виде:
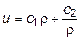 , (11.24)
, (11.24)
где с1 и с2 - постоянные интегрирования, которые определяются из граничных условий задачи:
при 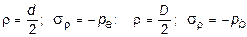 . (11.25)
. (11.25)
Подставляя выражение u из (11.24) в выражение sr из (11.22) с учетом граничных условий (11.25) получим:
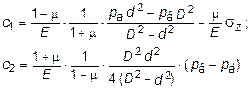 (11.26)
(11.26)
В результате совместного рассмотрения (11.22), (11.24) и (11.26) выражения для напряжения примут окончательный вид:
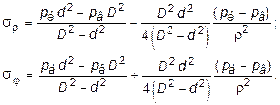 (11.27)
(11.27)
Рассмотрим случай нагружения цилиндра только внутренним давлением, тогда принимая pв = 0, из (11.21) и (11.27) получим:
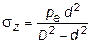 ;
;
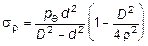 ; (11.28)
; (11.28)
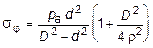 .
.
Анализ выражений (11.28) показывает, что sj > sz > sr Следовательно sj = s1; sz = s2; sr = s3 . Выражение интенсивности напряжения в данном случае принимает вид:
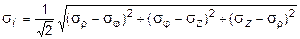 .
.
Из (11.28), учитывая, что
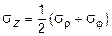 . (11.28¢)
. (11.28¢)
получим
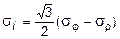 . (11.29)
. (11.29)
Предположим, что цилиндр изготовлен из неупрочняющегося материала для которого условие пластичности выражается в следующем виде:
si = sT , (11.30)
где sT - предел текучести материала цилиндра.
Подставляя (11.29) в (11.30) получим условия пластичности для данного случая:
sj - sr = 2 K, (11.31)
где 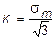 .
.
Из анализа выражений напряжений (11.28) следует вывод, что наибольшее значение напряжение sj принимает при r = d/2, т.е. на внутренней границе цилиндра. Следовательно, по мере увеличения внутреннего давления в пластическое состояние будут сначала переходить внутренние, а затем и более близкие к внешней границе слои материала.
Для определения значения давления, при котором слои на внутренней границе цилиндра, т.е. при r = d/2, переходят в пластическое состояние, воспользуемся условием пластичности (11.31), подставляя в него выражение напряжений из (11.28):
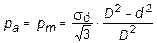 . (11.32)
. (11.32)
По мере дальнейшего роста внутреннего давления зона пластичных деформаций от внутренней поверхности распространяется в сторону наружной поверхности.
Для случая когда все поперечное сечение оболочки находится в пластическом состоянии рассматривается условие равновесия (11.18) и условие пластичности (11.31) и тогда:
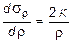 . (11.33)
. (11.33)
Проинтегрировав последнее уравнение, получим:
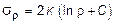 . (11.34)
. (11.34)
Постоянная интегрирования C определяется из граничных условий задачи:
r = D/2; sr = 0. (11.35)
Подставляя (11.34) в (11.35), определим: 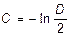 . Следовательно, из (11.34) окончательно получим:
. Следовательно, из (11.34) окончательно получим:
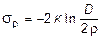 . (11.36)
. (11.36)
Из условия пластичности (11.31) будем иметь
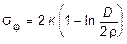 . (11.37)
. (11.37)
Выражение для sz принимает вид:
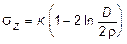 . (11.38)
. (11.38)
Величину внутреннего давления, при действии которого вся оболочка переходит в пластическое состояние, обозначим pа = РПР и получим из граничных условий задачи при r = d/2 РПР = sr Следовательно, из (11.36) получим:
РПР = 2 K ln 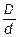 .
.
Дата добавления: 2015-12-29; просмотров: 1390;
