Пример расчета (задача № 14)
Для балки (рис. 6.11) задано: l1 = 2 l2 , P = q l1, m = q 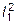 .
.
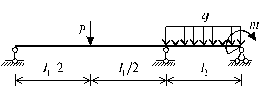 Рис. 6.11
Рис. 6.11
|
Требуется:
1. Определить степень статической неопределимости системы и составить уравнение совместности деформаций;
2. Определить коэффициенты и решить каноническое уравнение метода сил;
3. Построить эпюры моментов М и поперечных сил Q.
Решение
1. Определить степень статической неопределимости системы и составить уравнение совместности деформаций. Используя зависимость W из пункта 6.1, подсчитаем степень статической неопределимости системы. D = 1, Ш = 0, С = 4 ® W = 3×1 - 2×0 - 4= -1, следовательно система один раз статически неопределима. Основную систему получим путем отбрасывания опоры в точке А и замены ее действия неизвестным усилием X1 (рис. 6.12). Каноническое уравнение метода сил в данном случае запишется в следующем виде:
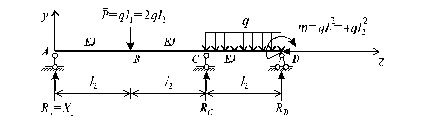
|
Рис. 6.12
d11 × X1 + D1P = 0.
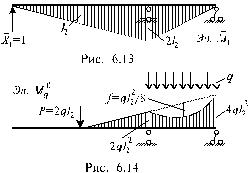
2. Определить коэффициенты и решить каноническое уравнение метода сил. От силы X1 строим эпюру M1 (рис. 6.13). Для определения величины d11 воспользуемся выражением (6.12). Фактически эпюру M1 нужно умножить саму на себя и проинтегрировать это произведение:
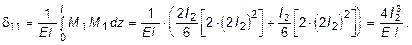
|
Для определения свободного коэффициента в каноническом уравнении строим в основной системе эпюру моментов MP от внешней нагрузки (рис. 6.14) и в соответствии с (6.7) получаем:
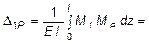
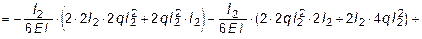
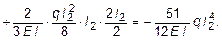
При вычислении D1P было учтено, что эпюры М1 и МP имеют разный знак, т.к. вызывают растяжение разных волокон - об этом говорит отрицательный знак при D1P . Кроме этого, криволинейный участок в эпюре МP был представлен как разность трапеции и параболического сегмента.
Напишем уравнение совместности деформаций в виде
E I d11 × X1 + E I D1P = 0,
и, подставляя найденные величины перемещений, получим:
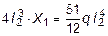 , откуда X1 =
, откуда X1 = 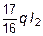 .
.
3. Построить эпюры изгибающих моментов и поперечных сил. Окончательную эпюру изгибающих моментов получим по формуле:
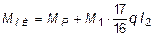 .
.
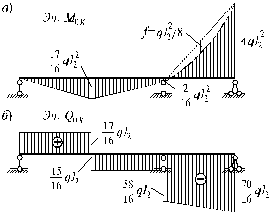 Рис. 6.15
Рис. 6.15
|
Последняя формула означает, что окончательное значение момента в любом сечении определяется путем сложения значения момента в эпюре МP с величиной момента в эпюре М1, увеличенной на коэффициент 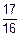 ql2 (рис. 6.15, а). Эпюру QОК для заданной системы можно построить следующим образом. Заменив в заданной системе опорные реакции RA на X1, получим статически определимую эквивалентную систему, тождественную заданной. Далее, определяя остальные опорные реакции RC и RD и по методу сечений составляя аналитические выражения изменения поперечных сил на каждом участке, по ним определив ординаты в характерных сечениях, строится эпюра QОК (рис. 6.15,б).
ql2 (рис. 6.15, а). Эпюру QОК для заданной системы можно построить следующим образом. Заменив в заданной системе опорные реакции RA на X1, получим статически определимую эквивалентную систему, тождественную заданной. Далее, определяя остальные опорные реакции RC и RD и по методу сечений составляя аналитические выражения изменения поперечных сил на каждом участке, по ним определив ординаты в характерных сечениях, строится эпюра QОК (рис. 6.15,б).
Дата добавления: 2015-12-29; просмотров: 782;
