ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, ЧЕРЕЗ НАСАДКИ И ВОДОСЛИВЫ
ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ МАЛОГО ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ ПРИ ПОСТОЯННОМ НАПОРЕ
Отверстие считают малым, если его размер по высоте значительно меньше напора — не более 0,1 Н. Тонкой стенкой считают такую, у которой отверстие имеет заостренную кромку; при этом струя,вытекающая из отверстия, преодолевает лишь местные сопротивления.
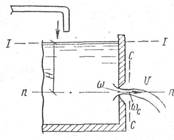
Рассмотрим сосуд, имеющий в вертикальной стенке отверстие площадью о, через которое вытекает жидкость под постоянным напором H (рис. 1.39). При вытекании струи жидкости из отверстия на некотором расстоянии от него наблюдается сжатие ее поперечного сечения. Отношение площади сжатого сечения ωcк площади отверстия ω называют коэффициентом сжатия:
(1.90)
|
| Рис. 1.39. Схема свободного истечения жидкости из малого отверстия в тонкой стенке |
По характеру сжатия струйное течение бывает полным, если струя получает сжатие по всему периметру отверстия, и неполным, если струя не имеет бокового сжатия с одной или нескольких сторон, например, когда отверстие примыкает к стенке или ко дну сосуда, которые при этом являются как бы направляющими для вытекающей струи.
Полное сжатие будет совершенным, если отверстие расположено на значительном расстоянии от боковых стенок и дна сосуда, так что они не оказывают влияния на сжатие струи (когда т. > 3а, где т — расстояние от стенок или дна, а — размер отверстия), и несовершенным, если па него оказывают влияние стенки или дно сосуда.
При истечении жидкости из отверстия задача сводится к определению скорости истечения и расхода жидкости. Составим уравнение Бернулли для сечений I-I и сc (сжатое сечение струи на рис. 1.39). За плоскость сравнения примем плоскость пи, проходящую через центры отверстия и сжатого сечения. Обозначая скорость движения на свободной поверхности через v0 и считая, что давление на свободной поверхности и в центре тяжести сжатого сечения равно атмосферному, получим:

Потери напора в рассматриваемом случае вызываются местным сопротивлением входа в отверстие
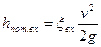


 Тогда
Тогда
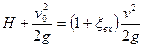
и далее
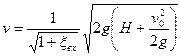 . (1.91)
. (1.91)
Принимая обозначения
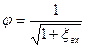 (1.92)
(1.92)
и
 , (1.93)
, (1.93)
окончательно получим:
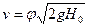 , (1.94)
, (1.94)
где φ— коэффициент скорости.
Если скорость v0 движения свободной поверхности мала, то формула получает более простой вид:
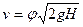 , (1.95)
, (1.95)
Коэффициент скорости φ для рассматриваемого случая принимают равным 0,97.
Расход через малое отверстие в тонкой стенке при постоянном напоре легко определить по формуле
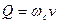 . (1.96)
. (1.96)
Подставляя в эту зависимость значения ωс из выражения (1.90) и v из выражения (1.94), получим:
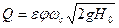 . (1.97)
. (1.97)
Произведение коэффициентов сжатия ε и скорости φ называют коэффициентом расхода отверстия μ, т. е.
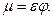
Окончательная формула для расхода через малое отверстие в тонкой стенке имеет такой вид:
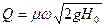 (1.98)
(1.98)
При v0 = 0 формула (1.98) принимает вид:
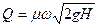 (1.99)
(1.99)
На основании многочисленных опытов установлено, что значение коэффициента μ при полном совершенном сжатии колеблется в пределах 0,59—0,63, составляя в среднем около 0,62. По последним исследованиям коэффициенты ε, φ и μ являются функциями числа Рейнольдса.

В расчетах обычно принимают следующие осредненные значения:
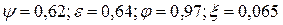
ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ МАЛОГО ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ ПРИ ПЕРЕМЕННОМ НАПОРЕ
Истечение жидкости при переменном напоре представляет собой один из примеров неустановившегося движения жидкости. Ниже приведено описание его двух простейших случаев.
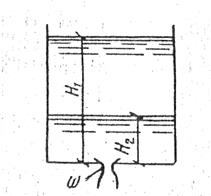
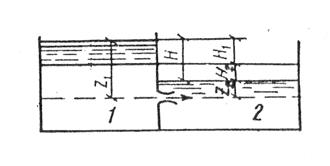
| Рис. 1.40 Схема опорожнения резервуара через отверстие в его дне | Рис. 1.41. Схема выравнивания уровней в сообщающихся сосудах |
Опорожнение резервуара. Рассмотрим заполненный жидкостью резервуар площадью горизонтального сечения 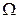 , в дне которого устроено отверстие площадью ω. Пусть при опорожнении резервуара начальный напор над центром тяжести отверстия был Н1, а конечный — Н2 (рис. 1.40). Если за время опорожнения резервуара притока жидкости не происходит, то опорожнение резервуара можно рассчитывать по формуле
, в дне которого устроено отверстие площадью ω. Пусть при опорожнении резервуара начальный напор над центром тяжести отверстия был Н1, а конечный — Н2 (рис. 1.40). Если за время опорожнения резервуара притока жидкости не происходит, то опорожнение резервуара можно рассчитывать по формуле
 . (1.100)
. (1.100)
Принимая в формуле (1.100) Н2 = 0, получим формулу для времени полного опорожнения резервуара:
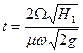 . (1.101)
. (1.101)
Зависимость (1.101) может быть представлена также в следующем виде:
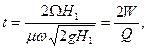 (1.102)
(1.102)
где W — объем резервуара; Q — расход жидкости при начальном напоре.
Следовательно, время полного опорожнения резервуара при переменном напоре в 2 раза больше времени, потребного для вытекания из резервуара того же количества жидкости при постоянном напоре, равном начальному напору H1
Выравнивание уровней в сообщающихся сосудах. Примем, что в начальный момент времени уровень в резервуаре 1 превышает уровень в резервуаре 2 на высоту Н (рис. 1.41).Обозначим площади горизонтальных сечений резервуаров I и 2 соответственно 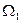 и
и 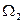 , напоры над центром тяжести отверстия соответственно z1 и z2 , их разность Н.
, напоры над центром тяжести отверстия соответственно z1 и z2 , их разность Н.
Время, потребное для полного выравнивания уровней жидкости в сообщающихся резервуарах 1 и 2, можно определить по формуле
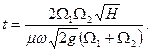 (1.103)
(1.103)
В результате выравнивания уровней в сообщающихся сосудах уровень в резервуаре 1 опустится на высоту Н1 а уровень в резервуаре 2 поднимется на высоту Н2.
Дата добавления: 2015-12-29; просмотров: 1830;
