УРАВНЕНИЕ РАВНОМЕРНОГО ДВИЖЕНИЯ ЖИДКОСТИ В КАНАЛАХ И ТРУБАХ

Уравнение равномерного движения жидкости устанавливает зависимость между силами сопротивления и потерями напора по дли­не канала или трубы.

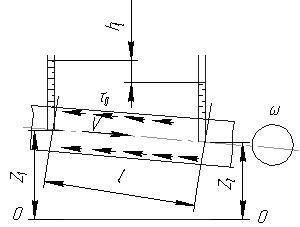
Рис.7.1. Схема к выводу уравнения равномерного движения жидкости

Рассмотрим равномерное движение жидкости в трубе па участ­ке l (рис.7.1.). Примем следующие обозначения:

ω — площадь живого сечения потока;

υ — средняя скорость движения жидкости;

γ — удельный вес жидкости;

χ — смоченный периметр;

R — гидравлический радиус;

τ₀ — сила трения на единице площади поверхности соприка­сания потока со стенками;

h_l — потери напора по длине.

Сила трения по всей поверхности выделенного участка равна:

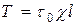. (1.49)

В единицу времени эта сила производит работу

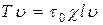. (1.50)

По закону сохранения энергии работа сил трения на поверхно­сти соприкасания равна энергии, затрачиваемой потоком на пре­одоление трения на рассматриваемом участке. Количество энергии, затраченной в единицу времени, отнесенное ко всему весу жидкости, равно

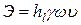. (1.51)

Приравнивая правые части уравнений (1.50) и (1.51), получим!

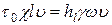(1.52)

или

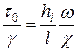. (1.53)

Как уже указывалось, отношение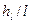

называется гидравлическим уклоном i, а отношение ω/χ — гидравлическим радиусом R. По­этому в окончательном виде можно записать:

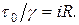(1.54)