ЗАДАЧА О ТРЕХ РЕЗЕРВУАРАХ

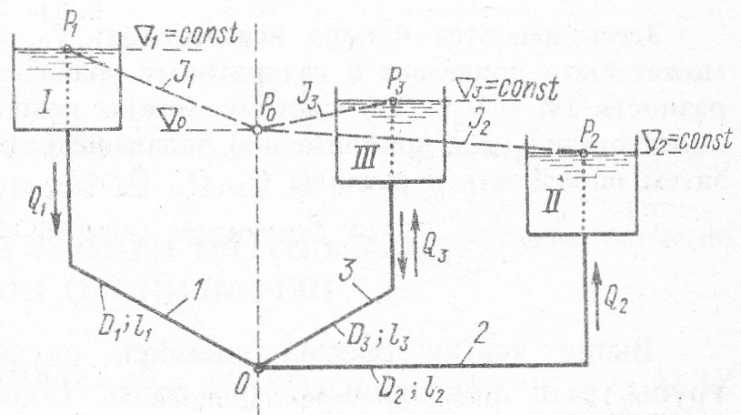
На рис. 5-16 представлены три резервуара (I, II, III), соединенные трубами. Обозначим через 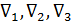отметки горизонтов воды соответственно в I, II и III резервуарах, причем эти отметки будем считать постоянными (неизменными во времени).

Дано: 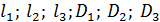; (а следовательно, K_l, К₂, К₃); .

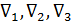Требуется найти: а) направление движения воды в трубе 3 (направления движения воды в трубах 1 и 2 известны заранее); б) расходы Q₁, Q₂, Q₃.

1°. О направлении движения воды в трубе 3. Покажем на чертеже пьезометрические линии для трех рассматриваемых труб, причем через 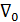обозначим отметку пьезометрической линии, отвечающую узловой точке О.

Рис. 5-16. К задаче о трех резервуарах

а) Если бак III питается водой из бака I, то вода по трубе 3 движется вверх, причем

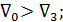
б) если бак III сам питает бак II,то вода в трубе 3 движется вниз, причем

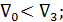
в) если в трубе 3 течения воды нет (бак III нейтрален), то

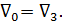
Чтобы установить, какой из грех перечисленных вариантов имеет место в данном конкретном случае, поступаем следующим образом:

1) задаемся условно величиной V0, равной V3:

Vo = V,.

2) В этом предположении, отвечающем случаю, когда бак III нейтрален, находим

расходы Q₁ и Q₂:

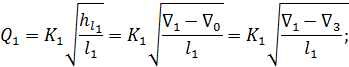
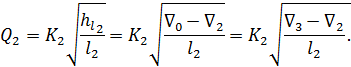
3) Сопоставляем между собой найденные Q₁ и Q₂. Если оказывается, что

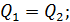
то бак III в действительности не работает (он нейтрален), и поэтому

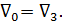
Если оказывается, что

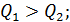
то в действительности

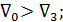
т. е. бак III питается из бака I и, следовательно, вода по трубе 3 поднимается вверх.

Если оказывается, что

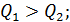
то в действительности

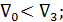
т. е. бак III питает бак II, причем вода в трубе 3 движется вниз.

2°. О величине расходов Q₁, Q₂, Q₃.Предположим, что имеется случай, когда бак III питает бак II. Учитывая (5-82), составляем следующую систему четырех уравнений:

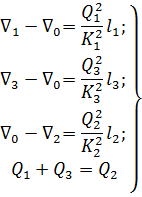
Здесь имеются четыре неизвестных: 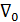, Q₁, Q₂, Q_3. Данная система уравнение может быть приведена к квадратному уравнению относительно разности 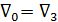или разности 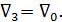Эту систему можно решать также путем подбора (или методом последовательного приближения), задаваясь различными значениями 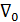. Найдя 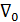, лет затем определить и расходы Q₁, Q₂, Q₃.

§ 5-10. ПОТЕРИ НАПОРА В СЛУЧАЕ РАСХОДА,