УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЖИДКОСТИ В НАПОРНЫХ ТРУБОПРОВОДАХ
§ 5-1. ПРЕДВАРИТЕЛЬНЫЕ УКАЗАНИЯ
Будем рассматривать установившееся, равномерное (параллельноструйное), напорное, турбулентное движение любой жидкости в круглых цилиндрических неподвижных трубах. Такой случай движения жидкости характеризуется условиями, поясненными в § 3-21 (п. 1°; рис. 3-28).
Внутренний диаметр труб обозначаем через D, длину их через /. Гидравлические элементы живого сечения рассматриваемого потока:
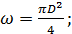
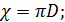
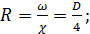 (5-1)
(5-1)
Главнейшие уравнения, которыми ниже будем пользоваться:
уравнение неразрывности — уравнение баланса расхода (3-38)—(3-40);
уравнение Бернулли — уравнение баланса удельной энергии (3-101);
3)уравнения для определения потерь напора (см. следующий параграф). Подчеркнем, что ниже будем иметь в виду исключительно случаи, отвечающие квадратичной области сопротивления.
Что касается трубопроводов, относящихся к доквадратичной области сопротивления и области гладких русел (труб), то расчет их отличается от расчетов, приводимых ниже, только тем, что при определении потерь напора вместо формулы Шези здесь приходится пользоваться исключительно формулой Вейсбаха—Дарси (4-70) и находить коэффициент трения λ, как указано в § 4-11.
§ 5-2. РАСЧЕТНЫЕ ЗАВИСИМОСТИ ДЛЯ ОПРЕДЕЛЕНИЯ ПОТЕРЬ НАПОРА
При расчете трубопроводов следует различать два случая.
1-й случай, когда местные потери напора отсутствуют или когда этими потерями можно пренебречь ввиду их малости сравнительно с потерями по длине (например, 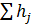 составляет величину, меньшую 5 % от потерь напора
составляет величину, меньшую 5 % от потерь напора 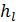 ).
).
В этом случае практически имеем только потери напора hl причем выражаем их через модуль расхода К согласно зависимости (4-105):
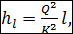 (5-2)
(5-2)
 (5-3)
(5-3)
Что касается величины 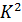 , то для круглой трубы
, то для круглой трубы
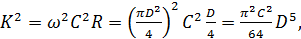 (5-4)
(5-4)
Где, согласно данным § 4-12, 5º,
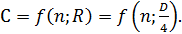 (5-5)
(5-5)
Таблица 5-1
Значения модуля расхода К и коэффициента гидравлического трения λ для новых битумизированных чугунных труб при Δ = (0,10 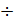 0,15) мм (квадратичная область сопротивления) 0,15) мм (квадратичная область сопротивления)
| |||||||||||||
| D, мм | Kмин. л/с | Kср. (л/с)2 | Кср, л/с | К2ср, (л/с)2 | Kмакс, л/с | К2макc,(л/с)2 | λмин | λср | λмакс | ||||
| 12,16 | 147,9 | 12,47 | 156,5 | 12,80 | 163,8 | 10,0230 | 0,0242 | 0,0255 | |||||
| 35,41 | 1,254- | 103 | 36,07 | 1,301 | 103 | 37,03 | 1,371 | 103 | 0,0209 | 0,0220 | 0,0230 | ||
| 74,96 | 5,619- | 105 | 76,16 | 5,800 | 103 | 77,70 | 6,037 | 103 | 0,0200 | 0,0208 | 0,0215 | ||
| 133,3 | 17,769- | 102 | 135,2 | 18,279- | 10з | 138,9 | 19,253 | 103 | 0,0190 | 0,0200 | 0,0206 | ||
| 214,2 | 45,882 | 103 | 219,3 | 48,092 | 103 | 227,8 | 51,893 | 103 | 0,0177 | 0,0191 | 0,0200 | ||
| 1 200 | 457,4 | 20,921 | 104 | 474,9 | 22,553 | 104 | 484J | 23,455 | 104 | 0,0165 | 0,0172 | 0,0185 | |
| 833,3 | 69,439 | 104 | 845,7 | 717531- | 104 | 859,3 | 73,840 | 104 | 0,0160 | 0,0165 | 0,0170 | ||
| 17,796- | 105 | 18,279- | 105 | 19,238 | 105 | 0,0153 | 0,0161 | 0,0165 | |||||
| .350 | 39,442- | 105 | 40,764- | 105 | 42,642 | 105 | 0,0149] | 0,0156 | 0,0161 | ||||
| 78,456 | 105 | 2 863 | 81,968 - | 105 | 85,498 | 105 | 0,0145 | 0,0151 | 0,0158 | ||||
| 14,569- | 106 | 3 878 | 15,039- | 106 | 3 924 | 15,398 | 106 | 0,0142 | 0,0148 | 0,0153 | |||
| 25,200 | 106 | 25,969 - | 106 | 26,967 | 106 | 0,0140 | 0,0145 | 0,0150 | |||||
| 65,270 | 106 | 66,733 | 106 | 8 377 | 70,174 | 106 | 0,0134 | 0,0141 | 0,0145 | ||||
| Г2008 | 14,419- | 107 | 15,009- | 107 | 12 596 | 15,866 | 107 | 0,0128 | 0,0136 | 0,0141 | |||
| 28,727 | 17 324 | 30,012- | 107 | 18 897 | 35,710 | 107 | 0,0125 | 0,0132 | 0,0138 | ||||
| 53,218- | 55,804- | 107 | 58,453 | 107 | 0,0122 | 0,0128 | 0,0134 | ||||||
| 93,104- | 31 102 | 96,733 | 107 | 100,68 | 107 | 0,0120 | 0,0125 | 0,0130 | |||||
Таблица 5-2
Значения модуля расхода К и коэффициента гидравлического трения λ, для новых небитумизированных чугунных труб при Δ = (0,25 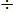 1,00) мм (квадратичная область сопротивления)
1,00) мм (квадратичная область сопротивления)
| D, мм | Kмин. л/с | Kср. (л/с)2 | Кср, л/с | К2ср, (л/с)2 | Kмакс, л/с | К2макc,(л/с)2 | λмин | λср | λмакс |
| 8,77 | 76,91 | 9,64 | 92,93 | 11,22 | 125,89 | 0,0300 | 0,0410 | 0,0490 | |
| 26,24 | 688,54 | 28,42 | 807,70 | 33,23 | 1104,2 | 0,0260 | 0,0350 | 0,0416 | |
| 56,40 | 3,1810-103 | 61,37 | 3,7663-103 | 70,94 | 5,0325-103 | 0,0240 | 0,0320 | 0,0380 | |
| 102,32 | 10,469-103 | 110,59 | 12,230 103 | 125,93 | 15,858-103 | 0,0230 | 0,0300 | 0,0350 | |
| 166,53 | 27,732-103 | 181,42 | 32,906 103 | 204,78 | 41,943-103 | 0,0220 | 0,0280 | 0,0330 | |
| 359,35 | 1,2913-105 | 391,36 | 1,5288-105 | 429,20 | 1,8421-105 | 0,0210 | 0,0255 | 0,0300 | |
| 649,83 | 4,2228-105 | 701,99 | 4,9280-105 | 770,71 | 5,9398-105 | 0,0200 | 0,0240 | 0,0280 | |
| 1059,4 | 11,223-105 | 1 128,3 | 12,724-105 | 1 242,7 | 15,443 105 | 0,0190 | 0,0230 | 0,0262 | |
| 1 588,6 | 25,237-105 | 1 684,8 | 28,383-105 | 1 878,4 | 35,285-105 | 0,0180 | 0,0224 | 0,0252 | |
| 2262,6 | 51,194-105 | 2 394,4 | 57,312-105 | 2 669,3 | 71,252-105 | 0,0170 | 0,0215 | 0,0242 | |
| 3 076,7 | 94,661-105 | 3 260,9 | 106,34-105 | 3 626,7 | 131,48-105 | 0,0168 | 0,0209 | 0,0235 | |
| 4054,7 | 16,439-106 | 4283,3 | 18,347-106 | 4776,7 | 22,810-106 | 0,0165 | 0,0206 | 0,0230 | |
| 6570,5 | 43,171 -106 | 6 860,5 | 47,066 106 | 7662,4 | 58,706-106 | 0,0160 | 0,0200 | 0,0221 | |
| 9788,8 | 95,824-106 | 105,25 106 | 130,99-106 | 0,0155 | 0,0192 | 0,0212 | |||
| 13 838 | 191,49-106 | 211,47-106 | 264,29 106 | 0,0150 | 0,0185 | 0,0207 | |||
| 18 759 | 351,91 -106 | 401,36-106 | 445,59 106 | 0,0147 | 0,0178 | 0,0203 | |||
| 605,31-106 | 26 704 | 713,10-106 | 28 895 | 834,92-106 | 0,0145 | 0,0170 | 0,0200 |
Согласно же данным § 4-12 и 4-10 для квадратичной области сопротивления
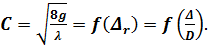 (5-6)
(5-6)
Таблица 5-3
Значение модуля расхода К и коэффициента гидравлического трения λ для бывших в эксплуатации чугунных труб при Δ = (1,0 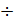 1,5) мм (квадратичная область сопротивления)
1,5) мм (квадратичная область сопротивления)
| D, мм | Kмин. л/с | Kср. (л/с)2 | Кср, л/с | К2ср, (л/с)2 | Kмакс, л/с | К2макc,(л/с)2 | λмин | λср | λмакс |
| 8,13 | 66,10 | 8,43 | 71,07 | 8,77 | 76,91 | 0;0490 | 0,0530 | 0,0570 | |
| 24,18 | 584,67 | 24,69 | 609,60 | 26,24 | 688.54 | 0,0416 | 0,0470 | 0,0490 | |
| 52,41 | 2,7468-103 | 53,90 | 2,9052-103 | 56,40 | 3,1810-103 | 0,0380 | 0,0416 | 0,0440 | |
| 95,23 | 9,0687-103 | 98,22 | 9,6472-103 | 102,32 | 10,469-103 | 0,0350 | 0,0380 | 0,0404 | |
| 155,48 | 24,162-103 | 160,62 | 25,799-103 | 166,53 | 27,732-103 | 0,0330 | 0,0356 | 0,0380 | |
| 336,59 | 1,1329-105 | 346,36 | 1,1997-105 | 359,35 | 1,2913-105 | 0,0300 | 0,0323 | 0,0342 | |
| 607,73 | 3,6934-105 | 627,74 | 3,9406-105 | 649,*83 | 4,2228-105 | 0,0280 | 0,0300 | 0,0320 | |
| 990,26 | 9,8062-105 | 1017,8 | 10,359 105 | 1 059,4 | 11,223-105 | 0,0262 | 0,0284 | 0,0300 | |
| 1491,0 | 22,231-105 | 1 534,6 | 23,550-105 | 1 588,6 | 25,237-105 | 0,0252 | 0,0270 | 0,0286 | |
| 2124,8 | 45,148-105 | 2195,5 | 48,202-105 | 2262,6 | 51,194- 105 | 0,0242 | 0,0257 | 0,0275 | |
| 2911,7 | 84,780-105 | 2980,9 | 88,858 -105 | 3076,7 | 94,661-105 | 0,0235 | 0,0250 | 0,0262 | |
| 3851,3 | 14,833-106 | 3954,0 | 15,634-106 | 4054,7 | 16,439-106 | 0,0230 | 0,0242 | 0,0255 | |
| 6278,2 | 39,415-106 | 6415,0 | 41,152-106 | 6570,5 | 43,171-106 | 0,0221 | 0,0232 | 0,0242 | |
| 9 370,0 | 87,797-106 | 9531,2 | 90,840-106 | 9788,8 | 95,824-106 | 0,0212 | 0,0224 | 0,0232 | |
| 174,59 106 | 181,910-106 | 13 838 | 191,49-106 | 0,0207 | 0,0218 | 0,0227 | |||
| 322,96 106 | 334,78-106 | 351,91-106 | 0,0203 | 0,0212 | 0,0221 | ||||
| 563,16-106 | 584,43-106 | 605,31-106 | 0,0200 | 0,0207 | 0,0215 |
Отсюда видно, что модуль расхода является функцией шероховатости и диаметра трубы. Если рассматривать, например, чугунные трубы, имеющие определенную шероховатость, то можно сказать, что для них модуль расхода является функцией только диаметра трубы. Имея это в виду, для чугунных труб приводятся таблицы (см. табл. 5-1, 5-2, 5-3), в которых величины К (и К2) даются в зависимости от D. По этим таблицам, зная D, можно определить К (или К2); и, наоборот, зная К (или К2), найти 1.
Необходимо запомнить, что каждая чугунная труба характеризуется определенным численным значением К : если задан диаметр D, то, следовательно, задана и величина К (ее берут из упомянутых таблиц). Зная К2, по формуле (5-2) легко находим hl. По формуле (5-2) можно решать и другие задачи; например, зная hl, К и l, расход Q и т. п.
2-й случай, когда имеются местные потери напора 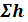 причем ими
причем ими
нельзя пренебрегать сравнительно с величиной hl. Здесь величину hl удобнее выражать через скоростной напор согласно зависимости Вейсбаха— Дарси (4-70):
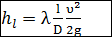 (5-7)
(5-7)
Величину λ следует определять, как указано в § 4-11. Для случая чугунных водопроводных труб разного диаметра величины λ, (относящиеся к квадратичной области сопротивления) приводятся в табл. 5-1, 5-2, 5-3.
Заметим, что под длиной l в формуле (5-7) обычно понимают длину всей трубы, предполагая здесь, что длины участков, на протяжении которых возникают местные потери напора, пренебрежимо малы (равны практически нулю). Что касается местных потерь 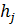 , то каждая такая потеря определяется по зависимости Вейсбаха (4-164):
, то каждая такая потеря определяется по зависимости Вейсбаха (4-164):
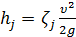 (5-8)
(5-8)
§ 5-3. СЛОЖЕНИЕ ПОТЕРЬ НАПОРА. ПОЛНЫЙ КОЭФФИЦИЕНТ СОПРОТИВЛЕНИЯ. ПОНЯТИЯ ДЛИННЫХ И КОРОТКИХ ТРУБОПРОВОДОВ
Представим на рис. 5-1 для примера некоторый трубопровод, имеющий по своей длине различные «местные препятствия» (в виде колена, задвижки, резкого расширения). Считаем, что расстояние между этими «препятствиями» достаточно велико: более (20 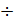 30) D (при этом взаимное
30) D (при этом взаимное
влияние имеющихся «препятствий» практически отсутствует; в противном случае оба «препятствия» следует рассматривать в совокупности - как одно).
Полная потеря напора hf на пути от сечения 1—1 до сечения 2 — 2 выразится в виде
hf =hl+Σhj.

| Рис. 5-1. Сложение потерь напора (при D = const) |
Рассмотрим отдельно каждое слагаемое этого выражения.
1. Сумма местных потерь напора Σhj. Из рис. 5-1 видно, что
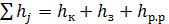 , (5-10)
, (5-10)
где hк — местная потеря в колене; hз — местная потеря в задвижке; hр.р. — местная потеря при резком расширении.
Согласно Вейсбаху,
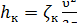 ;
; 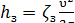 ;
; 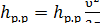 . (5-11)
. (5-11)
Следовательно,
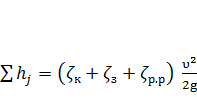 , (5-12)
, (5-12)
или в общем случае
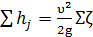 j (5-13)
j (5-13)
2. Потери напора по длине hl. Эти потери выражаются формулой (5-7). Введем обозначение:
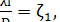 (5-14)
(5-14)
При этом hl представится в виде
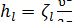 , (5-15)
, (5-15)
где  можно назвать коэффициентом сопротивления по длине.
можно назвать коэффициентом сопротивления по длине.
Как видно из (5-15), hl может быть выражена через скоростной напор.
3. Полная потеря напора hf. Подставляя в формулу (5-9) зависимости (5-13) и (5-15), получаем:
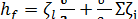 (5-16)
(5-16)
или
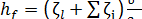 . (5-17)
. (5-17)
Вводя обозначение
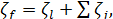 (5-18)
(5-18)
получаем, что
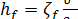 (5-19)
(5-19)
Это и есть окончательная формула для расчета п о л н ы х потерь напора (когда учитывают величину hl и величину Σhj).
Как видно, hf также выражается через скоростной напор.
Новый коэффициент ζf, учитывающий все потери напора на данной длине потока, назовем полным коэффициентом сопротивления.
Таким образом, на протяжении всего изложения, касающегося определения потерь напора в трубах, было введено три разных коэффициента сопротивления:
а) коэффициент местного сопротивления ζj для учета hj;
б) коэффициент сопротивления по длине ζl для учета hl;
в) полный коэффициент сопротивления ζf для учета hf.
При помощи этих коэффициентов соответствующие потери напора вы-
ражаются через скоростной напор.
Случай трубопровода переменного диаметра. Выше величину hf мы выражали через среднюю скорость υ, имея трубу постоянного диаметра, что позволило величину скоростного напора в зависимостях (5-12) и (5-17) выносить за скобки.
Положим,.что нам задан трубопровод переменного диаметра (рис. 5-2). Возникает вопрос, как в этом случае будут преобразовываться формулы (5-12) и (5-17).
Рассмотрим для примера сумму двух местных потерь, из которых первая (на резкое расширение) выражается через υ1 и вторая (на задвижку) - через υ2:
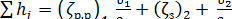 . (5-20)
. (5-20)
Первую местную потерю легко можно выразить также и через υ2. Действительно,
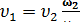 ; (5-21)
; (5-21)
следовательно
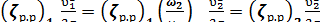 (5-22)
(5-22)
где
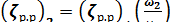 . (5-23)
. (5-23)
Таким образом, видно, что все слагаемые, входящие в выражение Σhj, могут быть всегда выражены через одну и ту же скорость, даже если труба будет переменного диаметра. При этом придется изменять только
величины 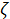 : умножить их на квадрат отношения с оответствующих площадей ω.
: умножить их на квадрат отношения с оответствующих площадей ω.
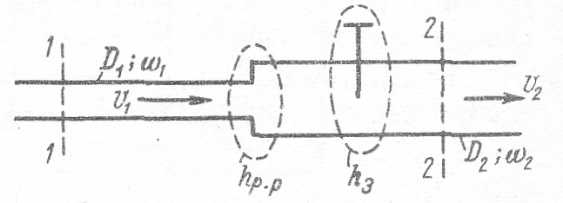
Рис. 5-2. Сложение потерь напора (при D ≠ const)
Выразив все слагаемые в формуле (5-12) или (5-17) через одну и ту же скорость υ, можем выносить в этих формулах скоростной напор за скобки так же, как и в случае трубопровода постоянного диаметра.
Понятия «длинного» и «короткого» трубопроводов. В случае достаточно длинных водопроводных труб величина Σhj по сравнению с величиной hl оказывается пренебрежимо малой, причем получается, что
hf ≈hl .
Такие трубы принято называть «длинными» в отличие от так называемых «коротких» труб, когда при расчете, помимо потерь напора по длине hh приходится учитывать еще местные потери напора Σhj.
В случае «длинных» трубопроводов при построении линий Е—Е и Р—Р обычно пренебрегают также и скоростным напором (ввиду его малости), считая, что напорная и пьезометрическая линии совпадают. Линия, в которую сливаются линии Е—Е и Р —Р, в этом случае обычно называется пьезометрической линией.
Принято считать, что в случае городских водопроводных труб (диаметром до 200—500 мм) длинный трубопровод получается, когда его длина более 200—1000 м. При меньшей длине местные потери напора часто могут составлять уже величину более 3 — 5% от потерь hl, причем их приходится учитывать.
А. КОРОТКИЕ ТРУБОПРОВОДЫ
§ 5-4. ПРОСТОЙТРУБОПРОВОД ПОСТОЯННОГО ДИАМЕТРА
Простым трубопроводом называется трубопровод, не имеющий боковых ответвлений.
1°. Случай истечения жидкости под уровень (рис 5-3, а). Рассматриваем установившееся движение: скорость υ в трубопроводе не изменяется во времени; разность Z уровней в сосудах А и В, соединяемых трубопроводом, постоянна (считаем, что в сосуд А жидкость все время каким-либо образом доливается, а из сосуда В — удаляется).
Найдем величину расхода Q для трубопровода. С этой целью используем уравнение Бернулли, следуя той схеме, которая пояснялась ранее (см. стр. 115):
1) намечаем живые сечения 1 — 1 и 2—2 (рис. 5-3, а): для этих сечений известно давление (р=ра) и, кроме того, известны скорости (υА≈υВ≈0);
2) намечаем плоскость сравнения 00; эту плоскость удобно провести по сечению 2—2; при этом z2 обратится в нуль;
3) пишем уравнение Бернулли
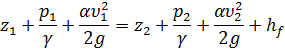

Рис. 5-3. Короткий трубопровод: а — истечение под уровень; б — истечение в атмосферу
4) выясняем значения отдельных членов, входящих в это уравнение:
z1 = Z; υ1 = υA = 0; υ2 = υB = 0; p1 = р2 = pa; z2 = 0; α ≈ 1,0, (5-25)
где Z — разность уровней жидкости в сосудах А и В;
5) подставляем (5-25) в (5-24); при этом получаем
Z = hf. (5-26)
Как видно, при истечении под уровень разность уровней Z целиком расходуется (тратится) на потери напора в трубе.
Выразим теперь потерю напора hf через скорость υв трубе, используя формулу (5-19):
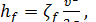 (5-27)
(5-27)
где ξf — полный коэффициент сопротивления для трубы.
Подставляя (5-27) в (5-26), имеем
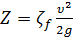 (5-28)
(5-28)
и, следовательно,
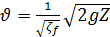 (5-29)
(5-29)
откуда
 (5-30)
(5-30)
2°. Случай истечения в атмосферу (рис. 5-3,6). Здесь также рассматриваем установившееся движение: υ = const; H = const, где H — превышение уровня жидкости в сосуде А над центром выходного сечения.
Используя уравнение Бернулли, сечения 1—1, 2—2 и плоскость сравнения 00 намечаем, как показано на чертеже. Имеем
z1 = H; υ1 = υA = 0; υ2 = υ; p1 = р2 = pa; α ≈ 1,0. (5-31)
Подставляя эти величины в уравнение Бернулли (5-24), получаем
 (5-32)
(5-32)
где υ—скорость в трубе, в частности в сечении 2—2.
Из рассмотрения (5-32) можно дать следующее правило: при истечении в атмосферу напор Н тратится (расходуется) на потери напора в трубе и на образование скоростного напора в выходном живом сечении.
Выражая по-прежнему hf формулой (5-27) и подставляя эту зависимость в (5-32), имеем
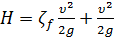 (5-33)
(5-33)
откуда
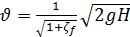 (5-34)
(5-34)
и, следовательно,
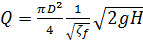 (5-35)
(5-35)
3°. Окончательные расчетные зависимости. Формулы (5-30) и (5-35) можно соответственно представить в виде следующих расчетных зависимостей:
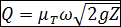 (5-36’)
(5-36’)
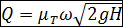 (5-36”)
(5-36”)
где μт равно:
а) при истечении под уровень [см. формулу (5-36’)]
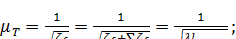 (5-37)
(5-37)
б) при истечении в атмосферу [см. формулу (5-36")]
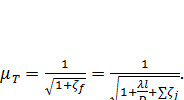 (5-38)
(5-38)
Коэффициент  называется коэффициентом расхода трубопровода.
называется коэффициентом расхода трубопровода.
Формулами (5-36’) и(5-36") и следует всегда пользоваться при расчете коротких простых трубопроводов постоянного диаметра. По этим формулам можно решать следующие практические задачи: 1) даны D иZ (или H), требуется найти Q; 2) даны D и Q, требуется найти Z (или H); 3) даны Q и Z (или H), требуется найти D. Последнюю задачу приходится решать подбором.
В отношении формулы (5-37) надо сделать следующее замечание.
При выводе ее мы располагали сечение 2—2 по уровню воды в сосуде В. При этом, составляя уравнение Бернулли (5-24), считали, что в полную потерю напора hl входят не только потери напора в самой трубе, но потеря напора на выход из трубы, т. е. та потеря, которая имеет место за трубой — в пределах сосуда В. Поэтому перепад Z при истечении под уровень, строго говоря, равен не потерям напора' в трубе, как условно отмечалось нами выше, а сумме потерь напора в трубе и в сосуде В.
Если бы при выводе формулы (5-37) сечение 2—2 намечалось не по уровню воды в сосуде В, а в конце самой трубы (так, как показано на рис. 5-3,б), то при этом для коэффициента расхода щ- при истечении под уровень мы получили бы формулу того же вида, что и при истечении в атмосферу [см. формулу (5-38)]. Только в этой формуле под величиной следовало бы понимать полный коэффициент сопротивления, подсчитанный без учета потерь напора на выход (т. е. без учета величины ζвых).
Таким образом, при расчете истечения под уровень можно пользоваться двумя разными способами, дающими, однако, один и тот же конечный результат.
1-й способ: коэффициент μT определяется по формуле (5-37); при этом под ζf понимаем полный коэффициент сопротивления, включающий коэффициент ζвых = 1,0.
2-й способ: коэффициент μT определяется, как и в случае истечения в атмосферу, по формуле (5-38); при этом под ζf понимаем полный коэффициент сопротивления, подсчитанный без учета величины ζвых = 1,0.
Дополнительно надо обратить внимание еще на следующие два обстоятельства.
1) При рассмотрении коротких трубопроводов длина начального участка трубы (см. рис. 4-21) может быть соизмерима с длиной всей трубы. При таком положении поясненный выше расчет короткого трубопровода оказывается несколько условным, поскольку формулы равномерного движения, которыми мы пользовались выше, строго говоря, не являются справедливыми для начального участка, где имеет место особый закон распределения скоростей по живым сечениям (впрочем в некоторых случаях превышение потерь напора в превышение потерь напора в пределах начального участка над потерями напора, возникающими при равномерном движении, может быть учтено коэффициентом сопротивления ζвх).
2) В § 3-17 было показано, что уравнение Бернулли применимо только к тем
сечениям трубопровода, для которых z +  = const, т. е. к сечениям, в пределах которых имеет место плавно изменяющееся движение.
= const, т. е. к сечениям, в пределах которых имеет место плавно изменяющееся движение.
Рассматривая сечение 2—2 на рис. 5-3,б, видим, что для этого сечения z +  ≠ const, поскольку как в верхней точке этого сечения, так и в нижней его точке лав.1ение равно рa. Отсюда заключаем, что в данном сечении мы имеем резко вменяющееся движение, к которому уравнение Вернул ли, строго говоря, неприменимо.
≠ const, поскольку как в верхней точке этого сечения, так и в нижней его точке лав.1ение равно рa. Отсюда заключаем, что в данном сечении мы имеем резко вменяющееся движение, к которому уравнение Вернул ли, строго говоря, неприменимо.
Более подробное рассмотрение вопроса об истечении жидкости из трубопровода в атмосферу приводит к следующим выводам (согласно А. И. Шварцу):
а) Эпюра скоростей υ в пределах концевого участка трубы (длиной lк; см. рис. 5-4) деформируется (по течению) и приобретает в сечении 2—2 несимметричный вид2, как то показано на рисунке.
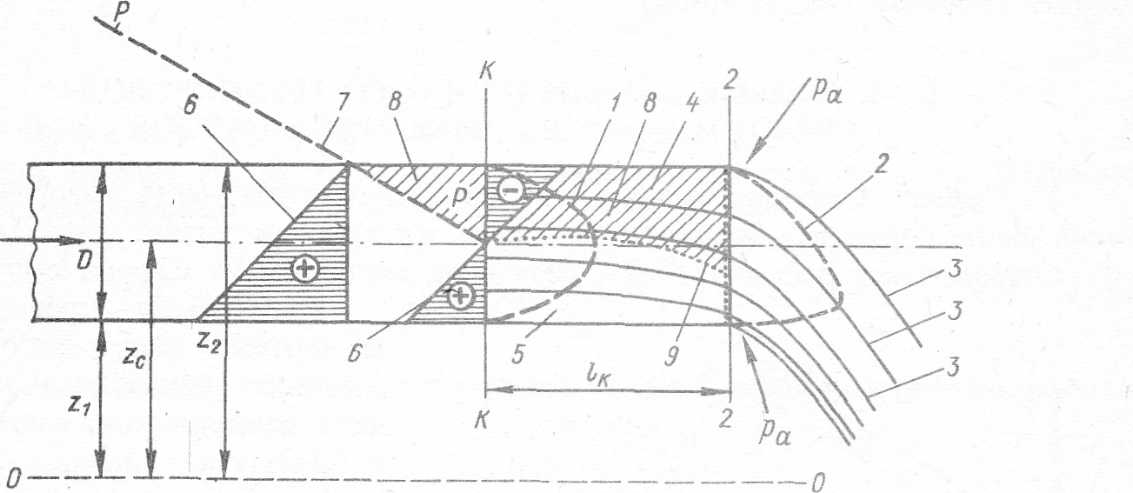
Рис. 5-4.Концевой участок трубы (при истечении в атмосферу)
1 — эпюра скоростей симметричная; 2 — то же, асимметричная; 3 — линия тока; 4 — элементарная струйка, верхняя расширяющаяся; 5 — то же, нижняя сужающаяся; 6 — эпюра давлений; 7 — пьезометрическая линия; 8 — область вакуума (покрыта наклонной штриховкой); 9 — приближенное положение линии атмосферного давления
б) В связи с этим линии тока 3 в пределах концевого участка должны искривляться, причем верхняя элементарная струйка 4 должна расширяться, а нижняя элементарная струйка 5 — сужаться. Напомним, что вдоль элементарной струйки расход δQ = const; поэтому при изменении скорости вдоль струйки площадь ее живого сечения также должна изменяться.
в) Рассматривая самую верхнюю расширяющуюся струйку 4,в конце которой давление атмосферное, видим, что в некотором сечении К — Кэтой струйки мы должны получить вакуум; для нижней же сужающейся струйки 5 будем иметь обратную картину (см. стр. 116-120).
г) В некотором предконцевом сечении К — К,удаленном от сечения 2—2 на расстояние lк (где эпюра скоростей 1 имеет уже симметричный вид) давление распределяется по гидростатическому закону (см. эпюру давления 6 в этом сечении). Как видно, для сечения К — Кимеем
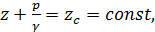
где zc — возвышение оси трубы над плоскостью сравнения 00.
д) Вопрос о длине lк концевого участка недостаточно исследован. Иногда длину lк считают равной, например, 1,5 D; однако такая рекомендация недостаточно проверена. Вместе с тем ясно, что при относительно малом диаметре трубы длиной участка (сравнительно с длиной всей трубы) можно пренебречь и условно считать, что предконцевое сечение К —К совпадает с выходным сечением 2—2. Именно этим допущением мы и пользовались при выводе уравнения (5-32).
Разумеется, в случае коротких труб большого диаметра вопрос о длине концевого участка, так же как и о длине начального участка (см. выше п. 1), может быть достаточно точно решен только на основании опытов.
4°. Замечания о напорной и пьезометрической линиях. На рис. 5-3,а в соответствии с указаниями, приведенными на стр. 116-120, построены линии E-E и Р-Р.
Подчеркнем, что строго говоря, эти линии в пределах участков, где возникает местные потери напора, являются кривыми. Однако в практике такого рода действительные кривые линии Е — Е и Р—Р аппроксимируют прямолинейными ломаными линиями образованными отрезками: а) прямыми наклонными и б) прямыми вертикальными (в виде «ступеней»), расположенными в тех местах, где возникают местные потери (и, разумеется, в местах расположения вертикальных участков трубопровода). При указанной аппроксимации, например, линии Е—Е, вертикальные ступени этой линии (для не вертикальных участков трубопровода) выражают величину местных потерь напора (точнее говоря, превышение местных потерь напора над потерей напора по длине соответствующего участка трубы).
§ 5-5. ОСОБЫЕ СЛУЧАИ ПРОСТОГО ТРУБОПРОВОДА: СИФОН И ВСАСЫВАЮЩАЯ ТРУБА НАСОСА
1°. Сифон. Сифоном называется самотечная труба, часть которой расположена выше горизонта жидкости в сосуде, который ее питает (рис 5-5).
Ограничимся рассмотрением истечения жидкости из сифона под уровень.
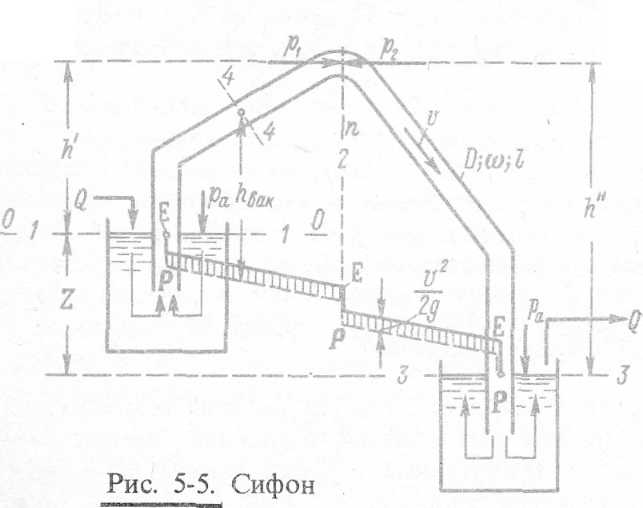
Если трубу, представленную на чертеже, каким-либо образом заполнить жидкостью, то после этого начнется движение жидкости из верхнего сосуда в нижний. В том, что жидкость в такой трубе будет двигаться, можно убедиться из следующего.
Наметим сечение трубы п-п и обозначим превышение его над горизонтом жидкости: в левом сосуде — через h’ и в правом сосуде — через h”. Если предположить, что жидкость, заполняющая сифон, находится в покое, то можем написать:
а) давление в сечении n - n с левой cтороны
p1 = pa +(-h’γ);
б) давление в сечении n –n с правой стороны
p2 = pa +(-h”γ);
где (—h') и (—h") — соответствующие заглубления сечения л—л под горизонтом жидкости в сосудах (эти заглубления отрицательны).
Как видно, p1 > р2;отсюда понятно, что жидкость в трубе не может находиться в покое: она будет двигаться слева направо, т. е. в сторону меньшего давления.
Рассмотрим установившееся движение жидкости в сифоне (Z = const). Наметим два сечения: 1 — 1и 3 — 3. Соединяя эти сечения уравнением Бернулли и рассуждая так же, как и в § 5-4, получим формулу для расхода Qв трубе в виде зависимости (5-36') и (5-37).
Характерным для сифона является то, что в нем имеет место вакуум. Наибольшая величина вакуума будет в сечении, наиболее высоко расположженном, т. е. в сечении n-n.
Найдем максимальную величину вакуума (hвак)макс в сифоне. С этой целью наметим по линии п —n, где ищем вакуум, сечение 2—2 и затем соединим сечения 1—1 и 2—2 уравнением Бернулли (плоскость сравнения проведем на уровне горизонта жидкости в левом сосуде):
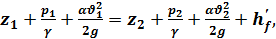 (5-39)
(5-39)
где
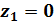 ;
; 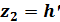 ;
; 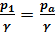 ;
; 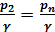 ;
;
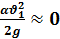 ;
;  ; (5-40)
; (5-40)
здесь υ; — скорость в трубе; рп — давление в сечении п — п.
Потери напора h'f на пути от сечения 1 — 1 до сечения 2—2 выражаем обычной зависимостью:
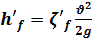 , (5-41)
, (5-41)
где ξ’f — полный коэффициент сопротивления, учитывающий потерю напора не во зеей трубе, а только от сечения 1—1 до сечения 2—2. Подставляя (5-40) и (5-41) в (5-39), получаем:
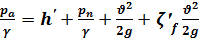 (5-42)
(5-42)
или
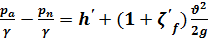 (5-43)
(5-43)
так как
 , (5-44)
, (5-44)
то
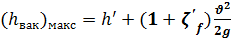 . (5-45)
. (5-45)
Пользуясь формулой (5-45), можно определить вакуум в любом сечении трубы, например в сечении 4 — 4. При этом в формуле (5-45) под величиной h’ следует понимать только превышение сечения 4—4 над горизонтом жидкости в левом сосуде, а под величиной ζ’f — полный коэффициент сопротивления, учитывающий потери напора от сечения 1 — 1 до сечения 4—4.
Из формулы (5-45)видно, что 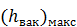 зависит от h’;если h’ будет велико,тои
зависит от h’;если h’ будет велико,тои 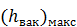 будет велико. При больших
будет велико. При больших 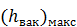 струя всифоне может разорваться, и сифон перестанет работать. Считают, что для нормальной работы сифона величина
струя всифоне может разорваться, и сифон перестанет работать. Считают, что для нормальной работы сифона величина 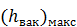 вычисленная по формуле (5-45), должна быть такой, при которой удовлетворяется условие
вычисленная по формуле (5-45), должна быть такой, при которой удовлетворяется условие
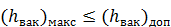 ,
,
где 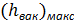 — вакуум, допустимый по условиям невозможности образования разрыва турбулентной струи (характеризуемой пульсацией давления).
— вакуум, допустимый по условиям невозможности образования разрыва турбулентной струи (характеризуемой пульсацией давления).
Величину 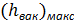 для воды (при нормальном атмосферном давлении) можно принять равной, например,
для воды (при нормальном атмосферном давлении) можно принять равной, например,
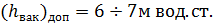
Анализируя вопрос о разрыве струи в сифоне, надо учитывать следующие обстоятельства.
1) В сифоне из жидкости должен выделяться растворенный воздух (в связи с уменьшением давления в районе сечения п — п; см. § 1-5). Этот воздух должен скопляться в виде воздушного «мешка» в верхней точке сечения п—п. Выпуск его через какой-либо клапан невозможен; при открытии отверстия (клапана) в районе сечения п — п атмосферный воздух будет поступать в трубу, увеличивая воздушный «мешок». Этот «мешок» может быть удален из сифона только при помощи особого насоса.
2) В формулу (5-45) входит средняя скорость υ, найденная исходя из осред-ненных во времени скоростей и. Поэтому 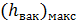 установленный по указанной формуле, является осредненным вакуумом. Мгновенный (актуальный) вакуум в какой-либо точке потока равен осредненному вакууму, увеличенному на так называемый п у л ь с а ц и о н н ы й вакуум (являющийся или положительным, или отрицательным). Из сказанного ясно, что мгновенные вакуумы в отдельных точках потока могут значительно превосходить величину (hвак)макс, вычисленную по формуле (5-45). Таким образом, можно утверждать, что кавитация потока (см. § 1-5) должна начаться ранее, чем осредненное давление рn, вычисленное по формуле (5-43), достигнет величины pн.п (давления насыщенных паров).
установленный по указанной формуле, является осредненным вакуумом. Мгновенный (актуальный) вакуум в какой-либо точке потока равен осредненному вакууму, увеличенному на так называемый п у л ь с а ц и о н н ы й вакуум (являющийся или положительным, или отрицательным). Из сказанного ясно, что мгновенные вакуумы в отдельных точках потока могут значительно превосходить величину (hвак)макс, вычисленную по формуле (5-45). Таким образом, можно утверждать, что кавитация потока (см. § 1-5) должна начаться ранее, чем осредненное давление рn, вычисленное по формуле (5-43), достигнет величины pн.п (давления насыщенных паров).
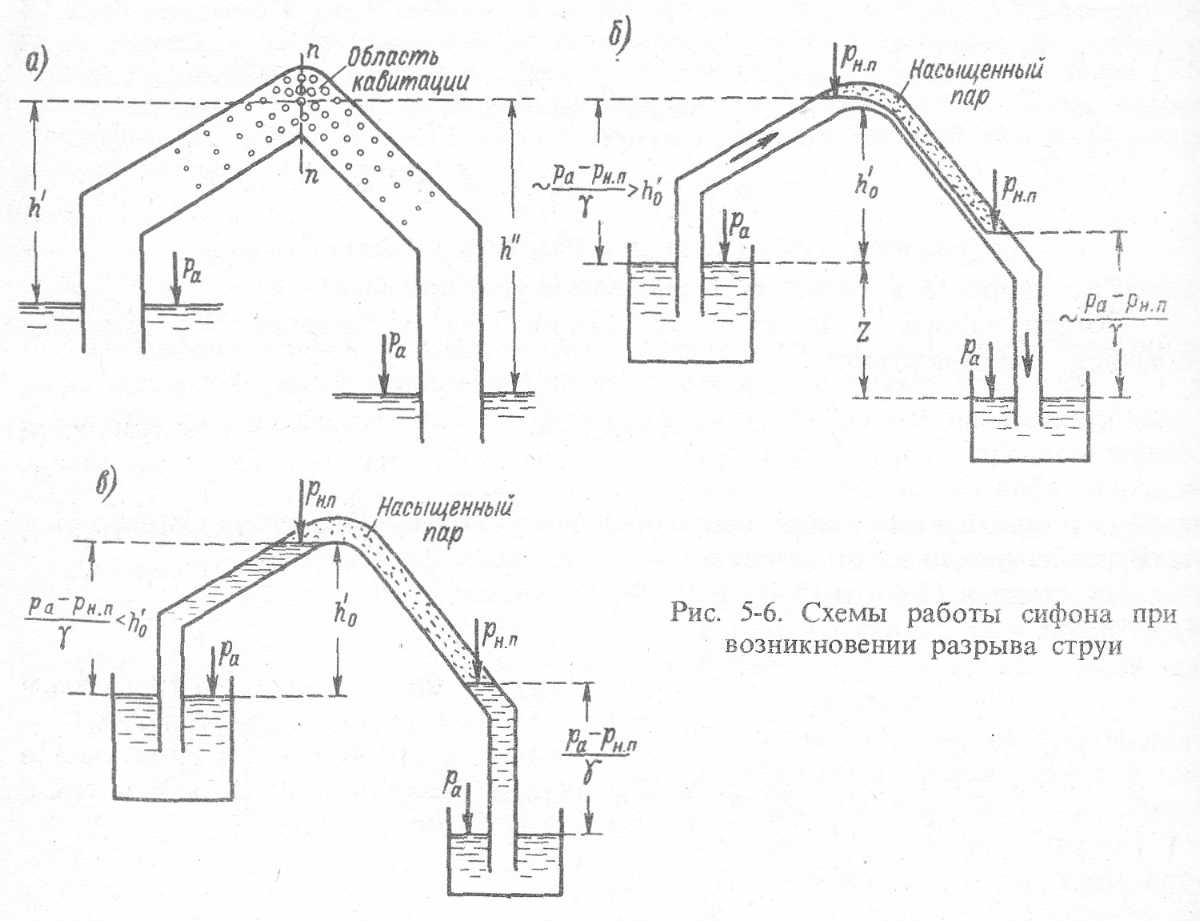
3) При достаточно большом h’ движение жидкости в сифоне следует представлять себе по схеме на рис. 5-6, а: наибольший объем кавитационных паровоздушных областей (с давлением паров ри.п) имеет место в сечении n — n. По мере движения жидкости от cечения n — n к выходу эти кавитационные области, увлекаемые потоком, закрываются и постепенно исчезают.
4) Увеличивая размер h’ (поднимая трубу сифона над сосудами), можно получить условия, когда объем паровоздушной области увеличится настолько, что мы получим картину, приближающуюся к схеме на рис. 5-6, б. Очевидно, здесь рассматриваемая труба уже не работает как сифон, причем расход Q в этом случае вовсе не зависит от разности Z уровней жидкости в сосудах.
При дальнейшем увеличении h’ произойдет полный разрыв струи, как показано на рис. 5-6, в.
5) Сечение n— n, где определялся максимальный вакуум, намечено на повороте (рис. 5-5). Условия движения жидкости на повороте носят особый характер (см. §4-19); здесь возникают центробежные силы, которые способствуют: увеличению давления (а следовательно, уменьшению вакуума) в верхней точке и уменьшению давления (а следовательно, увеличению вакуума) в нижней точке трубы. Благодаря этому вакуум в нижней точке может оказаться больше, чем в верхней точке трубы. Всех этих обстоятельств, связанных с поворотом трубы, формула (5-45) не учитывает.
В заключение отметим, что напорная линия Е — Е и пьезометрическая линия Р — Р в случае сифона выглядят, как показано на рис. 5-5: например,
первая «ступенька» линии Е — Е выражает потерю напора на вход в трубу, потерю по длине до первого поворота трубы и потерю напора в этом повороте. Полная потеря напора в сифоне равна Z. Линия Р — Р лежит ниже линии Е — Е на величину 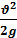
Превышение верха трубы над линией Р — Р, измеренное в любом вертикальном сечении выражает наибольший вакуум в соответствующем сечении трубы.
2°. Всасывающая труба насоса. «Всасывающей трубой» насоса называется труба, по которой насос засасывает жидкость из бассейна (рис. 5-7). Эта труба обычно так же, как и сифон, характеризуется наличием вакуума.
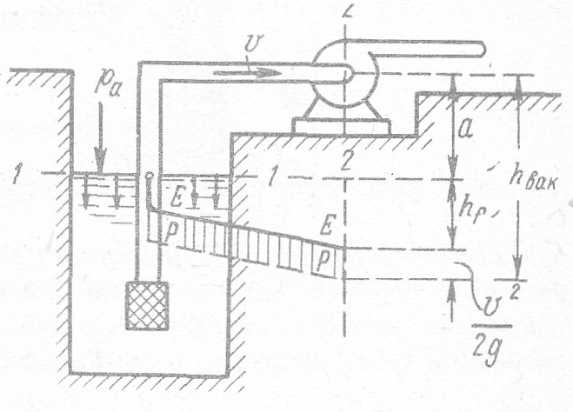
Рис. 5-7. Всасывающая труба насоса (потери напора во всасывающем клапане занижены — показаны не в масштабе)
Наибольшая величина вакуума будет непосредственно у насоса, перед его рабочим колесом1 (в сечении 2 — 2). Такой вакуум можно найти, соединяя уравнением Бернулли сечение 1—1, намеченное по поверхности жидкости в бассейне, и сечение 2 — 2. Его можно также определить по формуле (5-45), подставив в эту формулу вместо h’ величину a, означающую превышение оси насоса над горизонтом жидкости в бассейне, и вместо ξ’f величину ξ’f, т.е. полный коэффициент сопротивления, учитывающий потери напора во всей трубе. При этом получаем:
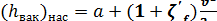 . (5-46)
. (5-46)
где  — вакуум перед рабочим колесом насоса.
— вакуум перед рабочим колесом насоса.
Если 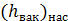 оказывается большим, то при этом возникает кавитация (см. § 1-5), которая обусловливает снижение коэффициента полезного действия насоса, а также эрозию лопастей насоса.
оказывается большим, то при этом возникает кавитация (см. § 1-5), которая обусловливает снижение коэффициента полезного действия насоса, а также эрозию лопастей насоса.
Различные типы насосов допускают различную величину вакуума. Обычно вакуум перед рабочим колесом насоса должен удовлетворять условию:
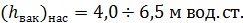 .
.
Величина допустимого вакуума зависит не только от типа насоса, но
и от температуры и рода жидкости. С увеличением температуры жидкости величина допустимого вакуума снижается. (Поскольку с повышением температуры кавитация усиливается; см. § 1-5.) Например, при температуре воды, равной 60 °С, допустимый вакуум приобретает уже отрицательное значение (т. е. насос должен работать при давлении в воде, большем атмосферного).
Зная допустимый вакуум для данного насоса и данной жидкости
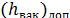 , можно по формуле (5-46) найти предельное максимальное возвышение насоса над горизонтом жидкости в бассейне:
, можно по формуле (5-46) найти предельное максимальное возвышение насоса над горизонтом жидкости в бассейне:
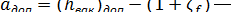 . (5-47)
. (5-47)
Для горячей воды aдоп может быть отрицательным; в этом случае насос приходится располагать ниже горизонта воды в колодце.
Дата добавления: 2015-12-29; просмотров: 2001;
